iterative scaling algorithm to equilibrate rows and column norms in matrices More...
Namespaces | |
| namespace | Architecture |
| namespace | HybridNonLinearSolverSpace |
| namespace | internal |
| namespace | LevenbergMarquardtSpace |
| namespace | numext |
Classes | |
| class | aligned_allocator |
| STL compatible allocator to use with with 16 byte aligned types. More... | |
| class | aligned_allocator_indirection |
| class | AlignedBox |
| An axis aligned box. More... | |
| class | AMDOrdering |
| class | AngleAxis |
| Represents a 3D rotation as a rotation angle around an arbitrary 3D axis. More... | |
| class | ArpackGeneralizedSelfAdjointEigenSolver |
| class | Array |
| General-purpose arrays with easy API for coefficient-wise operations. More... | |
| class | ArrayBase |
| Base class for all 1D and 2D array, and related expressions. More... | |
| class | ArrayWrapper |
| Expression of a mathematical vector or matrix as an array object. More... | |
| struct | ArrayXpr |
| class | AutoDiffJacobian |
| class | AutoDiffScalar |
| A scalar type replacement with automatic differentation capability. More... | |
| class | AutoDiffVector |
| class | BDCSVD |
| class Bidiagonal Divide and Conquer SVD More... | |
| class | BiCGSTAB |
| A bi conjugate gradient stabilized solver for sparse square problems. More... | |
| class | Block |
| Expression of a fixed-size or dynamic-size block. More... | |
| class | BlockImpl< const SparseMatrix< _Scalar, _Options, _Index >, BlockRows, BlockCols, true, Sparse > |
| class | BlockImpl< SparseMatrix< _Scalar, _Options, _Index >, BlockRows, BlockCols, true, Sparse > |
| class | BlockImpl< XprType, BlockRows, BlockCols, InnerPanel, Dense > |
| class | BlockImpl< XprType, BlockRows, BlockCols, InnerPanel, Sparse > |
| class | BlockImpl< XprType, BlockRows, BlockCols, true, Sparse > |
| class | CholmodBase |
| The base class for the direct Cholesky factorization of Cholmod. More... | |
| class | CholmodDecomposition |
| A general Cholesky factorization and solver based on Cholmod. More... | |
| class | CholmodSimplicialLDLT |
| A simplicial direct Cholesky (LDLT) factorization and solver based on Cholmod. More... | |
| class | CholmodSimplicialLLT |
| A simplicial direct Cholesky (LLT) factorization and solver based on Cholmod. More... | |
| class | CholmodSupernodalLLT |
| A supernodal Cholesky (LLT) factorization and solver based on Cholmod. More... | |
| class | CoeffBasedProduct |
| class | COLAMDOrdering |
| class | ColPivHouseholderQR |
| Householder rank-revealing QR decomposition of a matrix with column-pivoting. More... | |
| class | CommaInitializer |
| Helper class used by the comma initializer operator. More... | |
| class | ComplexEigenSolver |
| Computes eigenvalues and eigenvectors of general complex matrices. More... | |
| class | ComplexSchur |
| Performs a complex Schur decomposition of a real or complex square matrix. More... | |
| class | ConjugateGradient |
| A conjugate gradient solver for sparse self-adjoint problems. More... | |
| class | Cwise |
| Pseudo expression providing additional coefficient-wise operations. More... | |
| class | CwiseBinaryOp |
| Generic expression where a coefficient-wise binary operator is applied to two expressions. More... | |
| class | CwiseBinaryOpImpl< BinaryOp, Lhs, Rhs, Dense > |
| class | CwiseBinaryOpImpl< BinaryOp, Lhs, Rhs, Sparse > |
| class | CwiseNullaryOp |
| Generic expression of a matrix where all coefficients are defined by a functor. More... | |
| class | CwiseUnaryOp |
| Generic expression where a coefficient-wise unary operator is applied to an expression. More... | |
| class | CwiseUnaryOpImpl< UnaryOp, MatrixType, Sparse > |
| class | CwiseUnaryOpImpl< UnaryOp, XprType, Dense > |
| class | CwiseUnaryView |
| Generic lvalue expression of a coefficient-wise unary operator of a matrix or a vector. More... | |
| class | CwiseUnaryViewImpl< ViewOp, MatrixType, Dense > |
| class | CwiseUnaryViewImpl< ViewOp, MatrixType, Sparse > |
| struct | Dense |
| class | DenseBase |
| Base class for all dense matrices, vectors, and arrays. More... | |
| class | DenseCoeffsBase< Derived, DirectAccessors > |
| Base class providing direct read-only coefficient access to matrices and arrays. More... | |
| class | DenseCoeffsBase< Derived, DirectWriteAccessors > |
| Base class providing direct read/write coefficient access to matrices and arrays. More... | |
| class | DenseCoeffsBase< Derived, ReadOnlyAccessors > |
| Base class providing read-only coefficient access to matrices and arrays. More... | |
| class | DenseCoeffsBase< Derived, WriteAccessors > |
| Base class providing read/write coefficient access to matrices and arrays. More... | |
| struct | DenseFunctor |
| struct | DenseSparseProductReturnType |
| struct | DenseSparseProductReturnType< Lhs, Rhs, 1 > |
| class | DenseStorage |
| class | DenseStorage< T, 0, _Rows, _Cols, _Options > |
| class | DenseStorage< T, 0, _Rows, Dynamic, _Options > |
| class | DenseStorage< T, 0, Dynamic, _Cols, _Options > |
| class | DenseStorage< T, 0, Dynamic, Dynamic, _Options > |
| class | DenseStorage< T, Dynamic, _Rows, Dynamic, _Options > |
| class | DenseStorage< T, Dynamic, Dynamic, _Cols, _Options > |
| class | DenseStorage< T, Dynamic, Dynamic, Dynamic, _Options > |
| class | DenseStorage< T, Size, _Rows, Dynamic, _Options > |
| class | DenseStorage< T, Size, Dynamic, _Cols, _Options > |
| class | DenseStorage< T, Size, Dynamic, Dynamic, _Options > |
| class | DenseTimeSparseProduct |
| class | DenseTimeSparseSelfAdjointProduct |
| class | DGMRES |
| A Restarted GMRES with deflation. This class implements a modification of the GMRES solver for sparse linear systems. The basis is built with modified Gram-Schmidt. At each restart, a few approximated eigenvectors corresponding to the smallest eigenvalues are used to build a preconditioner for the next cycle. This preconditioner for deflation can be combined with any other preconditioner, the IncompleteLUT for instance. The preconditioner is applied at right of the matrix and the combination is multiplicative. More... | |
| class | Diagonal |
| Expression of a diagonal/subdiagonal/superdiagonal in a matrix. More... | |
| class | DiagonalBase |
| class | DiagonalMatrix |
| Represents a diagonal matrix with its storage. More... | |
| class | DiagonalPreconditioner |
| A preconditioner based on the digonal entries. More... | |
| class | DiagonalProduct |
| class | DiagonalWrapper |
| Expression of a diagonal matrix. More... | |
| class | DynamicSparseMatrix |
| A sparse matrix class designed for matrix assembly purpose. More... | |
| struct | ei_cleantype |
| struct | ei_cleantype< const T & > |
| struct | ei_cleantype< const T * > |
| struct | ei_cleantype< const T > |
| struct | ei_cleantype< T & > |
| struct | ei_cleantype< T * > |
| struct | ei_import_selector< Derived1, Derived2, false, false > |
| struct | ei_import_selector< Derived1, Derived2, false, true > |
| struct | ei_import_selector< Derived1, Derived2, true, true > |
| struct | ei_is_same_type |
| struct | ei_is_same_type< T, T > |
| struct | ei_lexi_comparison< Derived1, Derived2, 2 > |
| struct | ei_lexi_comparison< Derived1, Derived2, 3 > |
| struct | ei_lexi_comparison< Derived1, Derived2, 4 > |
| struct | ei_meta_false |
| struct | ei_meta_if |
| struct | ei_meta_if< false, Then, Else > |
| class | ei_meta_sqrt |
| class | ei_meta_sqrt< Y, InfX, SupX, true > |
| struct | ei_meta_true |
| struct | ei_quaternion_assign_impl< Other, 3, 3 > |
| struct | ei_quaternion_assign_impl< Other, 4, 1 > |
| struct | ei_to_vcgtype |
| struct | ei_traits |
| struct | ei_traits< AngleAxis< _Scalar > > |
| struct | ei_traits< Quaternion< _Scalar > > |
| struct | ei_traits< Rotation2D< _Scalar > > |
| struct | ei_transform_product_impl< Other, Dim, HDim, Dim, 1 > |
| struct | ei_transform_product_impl< Other, Dim, HDim, Dim, Dim > |
| struct | ei_transform_product_impl< Other, Dim, HDim, HDim, 1 > |
| struct | ei_transform_product_impl< Other, Dim, HDim, HDim, HDim > |
| struct | ei_unconst |
| struct | ei_unconst< const T > |
| struct | ei_unconst< T const & > |
| struct | ei_unconst< T const * > |
| struct | ei_unpointer |
| struct | ei_unpointer< T * > |
| struct | ei_unpointer< T *const > |
| struct | ei_unref |
| struct | ei_unref< T & > |
| struct | EigenBase |
| class | EigenSolver |
| Computes eigenvalues and eigenvectors of general matrices. More... | |
| class | Flagged |
| Expression with modified flags. More... | |
| class | ForceAlignedAccess |
| Enforce aligned packet loads and stores regardless of what is requested. More... | |
| class | FullPivHouseholderQR |
| Householder rank-revealing QR decomposition of a matrix with full pivoting. More... | |
| class | FullPivLU |
| LU decomposition of a matrix with complete pivoting, and related features. More... | |
| struct | general_product_to_triangular_selector< MatrixType, ProductType, UpLo, false > |
| struct | general_product_to_triangular_selector< MatrixType, ProductType, UpLo, true > |
| class | GeneralizedEigenSolver |
| Computes the generalized eigenvalues and eigenvectors of a pair of general matrices. More... | |
| class | GeneralizedSelfAdjointEigenSolver |
| Computes eigenvalues and eigenvectors of the generalized selfadjoint eigen problem. More... | |
| class | GeneralProduct< Lhs, Rhs, GemmProduct > |
| class | GeneralProduct< Lhs, Rhs, GemvProduct > |
| class | GeneralProduct< Lhs, Rhs, InnerProduct > |
| class | GeneralProduct< Lhs, Rhs, OuterProduct > |
| struct | GenericNumTraits |
| class | GMRES |
| A GMRES solver for sparse square problems. More... | |
| class | HessenbergDecomposition |
| Reduces a square matrix to Hessenberg form by an orthogonal similarity transformation. More... | |
| class | Homogeneous |
| Expression of one (or a set of) homogeneous vector(s) More... | |
| class | HouseholderQR |
| Householder QR decomposition of a matrix. More... | |
| class | HouseholderSequence |
| Sequence of Householder reflections acting on subspaces with decreasing size. More... | |
| class | HybridNonLinearSolver |
| Finds a zero of a system of n nonlinear functions in n variables by a modification of the Powell hybrid method ("dogleg"). More... | |
| class | Hyperplane |
| A hyperplane. More... | |
| class | IdentityPreconditioner |
| A naive preconditioner which approximates any matrix as the identity matrix. More... | |
| class | IncompleteCholesky |
| Modified Incomplete Cholesky with dual threshold. More... | |
| class | IncompleteLU |
| class | IncompleteLUT |
| Incomplete LU factorization with dual-threshold strategy. More... | |
| class | InnerStride |
| Convenience specialization of Stride to specify only an inner stride See class Map for some examples. More... | |
| class | IOFormat |
| Stores a set of parameters controlling the way matrices are printed. More... | |
| class | IterationController |
| Controls the iterations of the iterative solvers. More... | |
| class | IterativeSolverBase |
| Base class for linear iterative solvers. More... | |
| class | IterScaling |
| class | JacobiRotation |
| Rotation given by a cosine-sine pair. More... | |
| class | JacobiSVD |
| Two-sided Jacobi SVD decomposition of a rectangular matrix. More... | |
| class | KdBVH |
| A simple bounding volume hierarchy based on AlignedBox. More... | |
| class | KroneckerProduct |
| Kronecker tensor product helper class for dense matrices. More... | |
| class | KroneckerProductSparse |
| Kronecker tensor product helper class for sparse matrices. More... | |
| struct | LazyProductReturnType |
| class | LDLT |
| Robust Cholesky decomposition of a matrix with pivoting. More... | |
| class | LevenbergMarquardt |
| Performs non linear optimization over a non-linear function, using a variant of the Levenberg Marquardt algorithm. More... | |
| class | LLT |
| Standard Cholesky decomposition (LL^T) of a matrix and associated features. More... | |
| class | LU |
| class | Map |
| A matrix or vector expression mapping an existing array of data. More... | |
| class | Map< const Quaternion< _Scalar >, _Options > |
| Quaternion expression mapping a constant memory buffer. More... | |
| class | Map< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType >, _PacketAccess > |
| class | Map< Quaternion< _Scalar >, _Options > |
| Expression of a quaternion from a memory buffer. More... | |
| class | Map< Transpositions< SizeAtCompileTime, MaxSizeAtCompileTime, IndexType >, PacketAccess > |
| class | MapBase< Derived, ReadOnlyAccessors > |
| class | MapBase< Derived, WriteAccessors > |
| class | MappedSparseMatrix |
| Sparse matrix. More... | |
| class | Matrix |
| The matrix class, also used for vectors and row-vectors. More... | |
| class | MatrixBase |
| Base class for all dense matrices, vectors, and expressions. More... | |
| class | MatrixExponential |
| Class for computing the matrix exponential. More... | |
| struct | MatrixExponentialReturnValue |
| Proxy for the matrix exponential of some matrix (expression). More... | |
| class | MatrixFunction |
| Class for computing matrix functions. More... | |
| class | MatrixFunction< MatrixType, AtomicType, 0 > |
| class | MatrixFunction< MatrixType, AtomicType, 1 > |
| class | MatrixFunctionAtomic |
| Helper class for computing matrix functions of atomic matrices. More... | |
| class | MatrixFunctionReturnValue |
| Proxy for the matrix function of some matrix (expression). More... | |
| class | MatrixLogarithmAtomic |
| Helper class for computing matrix logarithm of atomic matrices. More... | |
| class | MatrixLogarithmReturnValue |
| Proxy for the matrix logarithm of some matrix (expression). More... | |
| class | MatrixMarketIterator |
| Iterator to browse matrices from a specified folder. More... | |
| class | MatrixPower |
| Class for computing matrix powers. More... | |
| class | MatrixPowerAtomic |
| class | MatrixPowerReturnValue |
| Proxy for the matrix power of some matrix (expression). More... | |
| class | MatrixPowerRetval |
| class | MatrixSquareRoot |
| Class for computing matrix square roots of general matrices. More... | |
| class | MatrixSquareRoot< MatrixType, 0 > |
| class | MatrixSquareRoot< MatrixType, 1 > |
| class | MatrixSquareRootQuasiTriangular |
| Class for computing matrix square roots of upper quasi-triangular matrices. More... | |
| class | MatrixSquareRootReturnValue |
| Proxy for the matrix square root of some matrix (expression). More... | |
| class | MatrixSquareRootTriangular |
| Class for computing matrix square roots of upper triangular matrices. More... | |
| class | MatrixWrapper |
| Expression of an array as a mathematical vector or matrix. More... | |
| struct | MatrixXpr |
| class | MetisOrdering |
| class | Minor |
| Expression of a minor. More... | |
| class | MINRES |
| A minimal residual solver for sparse symmetric problems. More... | |
| class | NaturalOrdering |
| class | NestByValue |
| Expression which must be nested by value. More... | |
| class | NoAlias |
| Pseudo expression providing an operator = assuming no aliasing. More... | |
| class | NumericalDiff |
| class | NumTraits |
| Holds information about the various numeric (i.e. scalar) types allowed by Eigen. More... | |
| struct | NumTraits< Array< Scalar, Rows, Cols, Options, MaxRows, MaxCols > > |
| struct | NumTraits< double > |
| struct | NumTraits< float > |
| struct | NumTraits< long double > |
| struct | NumTraits< short int > |
| struct | NumTraits< std::complex< _Real > > |
| struct | NumTraits< unsigned char > |
| class | OuterStride |
| Convenience specialization of Stride to specify only an outer stride See class Map for some examples. More... | |
| class | ParametrizedLine |
| A parametrized line. More... | |
| class | PardisoImpl |
| class | PardisoLDLT |
| A sparse direct Cholesky (LDLT) factorization and solver based on the PARDISO library. More... | |
| class | PardisoLLT |
| A sparse direct Cholesky (LLT) factorization and solver based on the PARDISO library. More... | |
| class | PardisoLU |
| A sparse direct LU factorization and solver based on the PARDISO library. More... | |
| class | PartialPivLU |
| LU decomposition of a matrix with partial pivoting, and related features. More... | |
| class | PartialReduxExpr |
| Generic expression of a partially reduxed matrix. More... | |
| class | PastixBase |
| class | PastixLDLT |
| A sparse direct supernodal Cholesky (LLT) factorization and solver based on the PaStiX library. More... | |
| class | PastixLLT |
| A sparse direct supernodal Cholesky (LLT) factorization and solver based on the PaStiX library. More... | |
| class | PastixLU |
| Sparse direct LU solver based on PaStiX library. More... | |
| class | PermutationBase |
| Base class for permutations. More... | |
| class | PermutationMatrix |
| Permutation matrix. More... | |
| struct | PermutationStorage |
| class | PermutationWrapper |
| Class to view a vector of integers as a permutation matrix. More... | |
| class | PlainObjectBase |
| Dense storage base class for matrices and arrays. More... | |
| class | PolynomialSolver |
| A polynomial solver. More... | |
| class | PolynomialSolver< _Scalar, 1 > |
| class | PolynomialSolverBase |
| Defined to be inherited by polynomial solvers: it provides convenient methods such as. More... | |
| class | ProductBase |
| class | ProductReturnType |
| Helper class to get the correct and optimized returned type of operator*. More... | |
| struct | ProductReturnType< Lhs, Rhs, CoeffBasedProductMode > |
| struct | ProductReturnType< Lhs, Rhs, LazyCoeffBasedProductMode > |
| class | QR |
| class | Quaternion |
| The quaternion class used to represent 3D orientations and rotations. More... | |
| class | QuaternionBase |
| Base class for quaternion expressions. More... | |
| class | RandomSetter |
| The RandomSetter is a wrapper object allowing to set/update a sparse matrix with random access. More... | |
| class | RealQZ |
| Performs a real QZ decomposition of a pair of square matrices. More... | |
| class | RealSchur |
| Performs a real Schur decomposition of a square matrix. More... | |
| class | Ref |
| A matrix or vector expression mapping an existing expressions. More... | |
| class | Ref< const TPlainObjectType, Options, StrideType > |
| class | RefBase |
| class | Replicate |
| Expression of the multiple replication of a matrix or vector. More... | |
| class | ReturnByValue |
| class | Reverse |
| Expression of the reverse of a vector or matrix. More... | |
| class | Rotation2D |
| Represents a rotation/orientation in a 2 dimensional space. More... | |
| class | RotationBase |
| Common base class for compact rotation representations. More... | |
| class | ScaledProduct |
| class | Scaling |
| Represents a possibly non uniform scaling transformation. More... | |
| class | Select |
| Expression of a coefficient wise version of the C++ ternary operator ?: More... | |
| struct | selfadjoint_product_selector< MatrixType, OtherType, UpLo, false > |
| struct | selfadjoint_product_selector< MatrixType, OtherType, UpLo, true > |
| struct | selfadjoint_rank1_update< Scalar, Index, ColMajor, UpLo, ConjLhs, ConjRhs > |
| struct | selfadjoint_rank1_update< Scalar, Index, RowMajor, UpLo, ConjLhs, ConjRhs > |
| class | SelfAdjointEigenSolver |
| Computes eigenvalues and eigenvectors of selfadjoint matrices. More... | |
| struct | SelfadjointProductMatrix< Lhs, 0, true, Rhs, RhsMode, false > |
| struct | SelfadjointProductMatrix< Lhs, LhsMode, false, Rhs, 0, true > |
| struct | SelfadjointProductMatrix< Lhs, LhsMode, false, Rhs, RhsMode, false > |
| class | SelfAdjointView |
| Expression of a selfadjoint matrix from a triangular part of a dense matrix. More... | |
| class | SelfCwiseBinaryOp |
| class | SimplicialCholesky |
| class | SimplicialCholeskyBase |
| A direct sparse Cholesky factorizations. More... | |
| class | SimplicialLDLT |
| A direct sparse LDLT Cholesky factorizations without square root. More... | |
| class | SimplicialLLT |
| A direct sparse LLT Cholesky factorizations. More... | |
| class | SkylineInplaceLU |
| Inplace LU decomposition of a skyline matrix and associated features. More... | |
| class | SkylineMatrix |
| The main skyline matrix class. More... | |
| class | SkylineMatrixBase |
| Base class of any skyline matrices or skyline expressions. More... | |
| struct | SkylineProductReturnType |
| class | SkylineStorage |
| struct | SluMatrix |
| struct | SluMatrixMapHelper< Matrix< Scalar, Rows, Cols, Options, MRows, MCols > > |
| struct | SluMatrixMapHelper< SparseMatrixBase< Derived > > |
| class | SparseDenseOuterProduct |
| struct | SparseDenseProductReturnType |
| struct | SparseDenseProductReturnType< Lhs, Rhs, 1 > |
| class | SparseDiagonalProduct |
| struct | SparseFunctor |
| class | SparseLU |
| Sparse supernodal LU factorization for general matrices. More... | |
| struct | SparseLUMatrixLReturnType |
| struct | SparseLUMatrixUReturnType |
| class | SparseMatrix |
| A versatible sparse matrix representation. More... | |
| class | SparseMatrixBase |
| Base class of any sparse matrices or sparse expressions. More... | |
| class | SparseQR |
| Sparse left-looking rank-revealing QR factorization. More... | |
| struct | SparseQR_QProduct |
| struct | SparseQRMatrixQReturnType |
| struct | SparseQRMatrixQTransposeReturnType |
| class | SparseSelfAdjointTimeDenseProduct |
| class | SparseSelfAdjointView |
| Pseudo expression to manipulate a triangular sparse matrix as a selfadjoint matrix. More... | |
| class | SparseSparseProduct |
| struct | SparseSparseProductReturnType |
| class | SparseSymmetricPermutationProduct |
| class | SparseTimeDenseProduct |
| class | SparseTriangularView |
| class | SparseVector |
| a sparse vector class More... | |
| class | SparseView |
| class | Spline |
| A class representing multi-dimensional spline curves. More... | |
| struct | SplineFitting |
| Spline fitting methods. More... | |
| struct | SplineTraits |
| struct | SplineTraits< Spline< _Scalar, _Dim, _Degree >, _DerivativeOrder > |
| Compile-time attributes of the Spline class for fixed degree. More... | |
| struct | SplineTraits< Spline< _Scalar, _Dim, _Degree >, Dynamic > |
| Compile-time attributes of the Spline class for Dynamic degree. More... | |
| class | SPQR |
| Sparse QR factorization based on SuiteSparseQR library. More... | |
| struct | SPQR_QProduct |
| struct | SPQRMatrixQReturnType |
| struct | SPQRMatrixQTransposeReturnType |
| struct | StdMapTraits |
| class | StdStemFunctions |
| Stem functions corresponding to standard mathematical functions. More... | |
| class | Stride |
| Holds strides information for Map. More... | |
| class | SuperLU |
| A sparse direct LU factorization and solver based on the SuperLU library. More... | |
| class | SuperLUBase |
| The base class for the direct and incomplete LU factorization of SuperLU. More... | |
| class | SVD |
| Standard SVD decomposition of a matrix and associated features. More... | |
| class | SVDBase |
| Mother class of SVD classes algorithms. More... | |
| class | SwapWrapper |
| class | Transform |
| Represents an homogeneous transformation in a N dimensional space. More... | |
| class | Translation |
| Represents a translation transformation. More... | |
| class | Transpose |
| Expression of the transpose of a matrix. More... | |
| class | Transpose< PermutationBase< Derived > > |
| class | Transpose< TranspositionsBase< TranspositionsDerived > > |
| class | TransposeImpl< MatrixType, Dense > |
| class | TransposeImpl< MatrixType, Sparse > |
| class | Transpositions |
| Represents a sequence of transpositions (row/column interchange) More... | |
| class | TranspositionsBase |
| class | TranspositionsWrapper |
| class | TriangularBase |
| struct | TriangularProduct< Mode, false, Lhs, true, Rhs, false > |
| struct | TriangularProduct< Mode, LhsIsTriangular, Lhs, false, Rhs, false > |
| struct | TriangularProduct< Mode, true, Lhs, false, Rhs, true > |
| class | TriangularView |
| Base class for triangular part in a matrix. More... | |
| class | Tridiagonalization |
| Tridiagonal decomposition of a selfadjoint matrix. More... | |
| class | Triplet |
| A small structure to hold a non zero as a triplet (i,j,value). More... | |
| class | UmfPackLU |
| A sparse LU factorization and solver based on UmfPack. More... | |
| class | UniformScaling |
| class | VectorBlock |
| Expression of a fixed-size or dynamic-size sub-vector. More... | |
| class | VectorwiseOp |
| Pseudo expression providing partial reduction operations. More... | |
| class | WithFormat |
| Pseudo expression providing matrix output with given format. More... | |
Typedefs | |
| typedef Transform< double, 2, Affine > | Affine2d |
| typedef Transform< float, 2, Affine > | Affine2f |
| typedef Transform< double, 3, Affine > | Affine3d |
| typedef Transform< float, 3, Affine > | Affine3f |
| typedef Transform< double, 2, AffineCompact > | AffineCompact2d |
| typedef Transform< float, 2, AffineCompact > | AffineCompact2f |
| typedef Transform< double, 3, AffineCompact > | AffineCompact3d |
| typedef Transform< float, 3, AffineCompact > | AffineCompact3f |
| typedef DiagonalMatrix< double, 2 > | AlignedScaling2d |
| typedef DiagonalMatrix< float, 2 > | AlignedScaling2f |
| typedef DiagonalMatrix< double, 3 > | AlignedScaling3d |
| typedef DiagonalMatrix< float, 3 > | AlignedScaling3f |
| typedef AngleAxis< double > | AngleAxisd |
| typedef AngleAxis< float > | AngleAxisf |
| typedef EIGEN_DEFAULT_DENSE_INDEX_TYPE | DenseIndex |
| typedef Transform< double, 2, Isometry > | Isometry2d |
| typedef Transform< float, 2, Isometry > | Isometry2f |
| typedef Transform< double, 3, Isometry > | Isometry3d |
| typedef Transform< float, 3, Isometry > | Isometry3f |
| typedef Transform< double, 2, Projective > | Projective2d |
| typedef Transform< float, 2, Projective > | Projective2f |
| typedef Transform< double, 3, Projective > | Projective3d |
| typedef Transform< float, 3, Projective > | Projective3f |
| typedef Quaternion< double > | Quaterniond |
| typedef Quaternion< float > | Quaternionf |
| typedef Map< Quaternion < double >, Aligned > | QuaternionMapAlignedd |
| typedef Map< Quaternion< float > , Aligned > | QuaternionMapAlignedf |
| typedef Map< Quaternion < double >, 0 > | QuaternionMapd |
| typedef Map< Quaternion< float >, 0 > | QuaternionMapf |
| typedef Rotation2D< double > | Rotation2Dd |
| typedef Rotation2D< float > | Rotation2Df |
| typedef Scaling< double, 2 > | Scaling2d |
| typedef Scaling< float, 2 > | Scaling2f |
| typedef Scaling< double, 3 > | Scaling3d |
| typedef Scaling< float, 3 > | Scaling3f |
| typedef Spline< double, 2 > | Spline2d |
| 2D double B-spline with dynamic degree. | |
| typedef Spline< float, 2 > | Spline2f |
| 2D float B-spline with dynamic degree. | |
| typedef Spline< double, 3 > | Spline3d |
| 3D double B-spline with dynamic degree. | |
| typedef Spline< float, 3 > | Spline3f |
| 3D float B-spline with dynamic degree. | |
| typedef Transform< double, 2 > | Transform2d |
| typedef Transform< float, 2 > | Transform2f |
| typedef Transform< double, 3 > | Transform3d |
| typedef Transform< float, 3 > | Transform3f |
| typedef Translation< double, 2 > | Translation2d |
| typedef Translation< float, 2 > | Translation2f |
| typedef Translation< double, 3 > | Translation3d |
| typedef Translation< float, 3 > | Translation3f |
Enumerations | |
| enum | { Large = 2, Small = 3 } |
| enum | { DontAlignCols = 1 } |
| enum | { StreamPrecision = -1, FullPrecision = -2 } |
| enum | { Lower = 0x1, Upper = 0x2, UnitDiag = 0x4, ZeroDiag = 0x8, UnitLower = UnitDiag|Lower, UnitUpper = UnitDiag|Upper, StrictlyLower = ZeroDiag|Lower, StrictlyUpper = ZeroDiag|Upper, SelfAdjoint = 0x10, Symmetric = 0x20 } |
| enum | { Unaligned = 0, Aligned = 1 } |
| enum | { DefaultTraversal, LinearTraversal, InnerVectorizedTraversal, LinearVectorizedTraversal, SliceVectorizedTraversal, InvalidTraversal, AllAtOnceTraversal } |
| enum | { NoUnrolling, InnerUnrolling, CompleteUnrolling } |
| enum | { Specialized, BuiltIn } |
| enum | { ColMajor = 0, RowMajor = 0x1, AutoAlign = 0, DontAlign = 0x2 } |
| enum | { OnTheLeft = 1, OnTheRight = 2 } |
| enum | { IsDense = 0, IsSparse } |
| enum | { CoeffBasedProductMode, LazyCoeffBasedProductMode, OuterProduct, InnerProduct, GemvProduct, GemmProduct } |
| enum | { IsSkyline = SkylineBit } |
| enum | { SPD = 0x100, NonSymmetric = 0x0 } |
| enum | AccessorLevels { ReadOnlyAccessors, WriteAccessors, DirectAccessors, DirectWriteAccessors } |
| enum | Action { GetAction, SetAction } |
| enum | AdditionalProductEvaluationMode { SkylineTimeDenseProduct, SkylineTimeSkylineProduct, DenseTimeSkylineProduct } |
| enum | CholmodMode { CholmodAuto, CholmodSimplicialLLt, CholmodSupernodalLLt, CholmodLDLt } |
| enum | ComputationInfo { Success = 0, NumericalIssue = 1, NoConvergence = 2, InvalidInput = 3 } |
| enum | CornerType { TopLeft, TopRight, BottomLeft, BottomRight } |
| enum | DecompositionOptions { Pivoting = 0x01, NoPivoting = 0x02, ComputeFullU = 0x04, ComputeThinU = 0x08, ComputeFullV = 0x10, ComputeThinV = 0x20, EigenvaluesOnly = 0x40, ComputeEigenvectors = 0x80, EigVecMask = EigenvaluesOnly | ComputeEigenvectors, Ax_lBx = 0x100, ABx_lx = 0x200, BAx_lx = 0x400, GenEigMask = Ax_lBx | ABx_lx | BAx_lx } |
| enum | Default_t { Default } |
| enum | DirectionType { Vertical, Horizontal, BothDirections } |
| enum | NoChange_t { NoChange } |
| enum | NumericalDiffMode { Forward, Central } |
| enum | QRPreconditioners { NoQRPreconditioner, HouseholderQRPreconditioner, ColPivHouseholderQRPreconditioner, FullPivHouseholderQRPreconditioner } |
| enum | Sequential_t { Sequential } |
| enum | SimplicialCholeskyMode { SimplicialCholeskyLLT, SimplicialCholeskyLDLT } |
| enum | TransformTraits { Isometry = 0x1, Affine = 0x2, AffineCompact = 0x10 | Affine, Projective = 0x20 } |
Functions | |
| template<typename DerTypeA , typename DerTypeB > | |
| const AutoDiffScalar< Matrix < typename internal::traits < DerTypeA >::Scalar, Dynamic, 1 > > | atan2 (const AutoDiffScalar< DerTypeA > &a, const AutoDiffScalar< DerTypeB > &b) |
| template<typename DerType , typename T > | |
| AutoDiffScalar< DerType > (min)(const AutoDiffScalar< DerType > &x | |
| T | AutoDiffScalar< DerType > (max)(const AutoDiffScalar< DerType > &x |
| template<typename SplineType , typename DerivativeType > | |
| void | basisFunctionDerivativesImpl (const SplineType &spline, typename SplineType::Scalar u, DenseIndex order, DerivativeType &N_) |
| template<typename Scalar , int Dim> | |
| AlignedBox< Scalar, Dim > | bounding_box (const Matrix< Scalar, Dim, 1 > &v) |
| template<typename BVH , typename Intersector > | |
| void | BVIntersect (const BVH &tree, Intersector &intersector) |
| template<typename BVH1 , typename BVH2 , typename Intersector > | |
| void | BVIntersect (const BVH1 &tree1, const BVH2 &tree2, Intersector &intersector) |
| template<typename BVH , typename Minimizer > | |
| Minimizer::Scalar | BVMinimize (const BVH &tree, Minimizer &minimizer) |
| template<typename BVH1 , typename BVH2 , typename Minimizer > | |
| Minimizer::Scalar | BVMinimize (const BVH1 &tree1, const BVH2 &tree2, Minimizer &minimizer) |
| template<typename Polynomial > | |
| NumTraits< typename Polynomial::Scalar >::Real | cauchy_max_bound (const Polynomial &poly) |
| template<typename Polynomial > | |
| NumTraits< typename Polynomial::Scalar >::Real | cauchy_min_bound (const Polynomial &poly) |
| template<typename Scalar > | |
| std::complex< Scalar > | cdiv (const Scalar &xr, const Scalar &xi, const Scalar &yr, const Scalar &yi) |
| template<typename PointArrayType , typename KnotVectorType > | |
| void | ChordLengths (const PointArrayType &pts, KnotVectorType &chord_lengths) |
| Computes chord length parameters which are required for spline interpolation. | |
| template<typename DerType > | |
| const AutoDiffScalar< DerType > & | conj (const AutoDiffScalar< DerType > &x) |
| template<typename SplineType , typename DerivativeType > | |
| void | derivativesImpl (const SplineType &spline, typename SplineType::Scalar u, DenseIndex order, DerivativeType &der) |
| void | dsaupd_ (int *ido, char *bmat, int *n, char *which, int *nev, double *tol, double *resid, int *ncv, double *v, int *ldv, int *iparam, int *ipntr, double *workd, double *workl, int *lworkl, int *info) |
| void | dseupd_ (int *rvec, char *All, int *select, double *d, double *z, int *ldz, double *sigma, char *bmat, int *n, char *which, int *nev, double *tol, double *resid, int *ncv, double *v, int *ldv, int *iparam, int *ipntr, double *workd, double *workl, int *lworkl, int *ierr) |
| template<typename T > | |
| NumTraits< T >::Real | ei_abs (const T &x) |
| template<typename T > | |
| NumTraits< T >::Real | ei_abs2 (const T &x) |
| template<typename T > | |
| void | ei_aligned_delete (T *ptr, size_t size) |
| void | ei_aligned_free (void *ptr) |
| void * | ei_aligned_malloc (size_t size) |
| template<typename T > | |
| T * | ei_aligned_new (size_t size) |
| void * | ei_aligned_realloc (void *ptr, size_t new_size, size_t old_size) |
| template<typename T > | |
| T | ei_atan2 (const T &x, const T &y) |
| template<bool Align> | |
| void | ei_conditional_aligned_free (void *ptr) |
| template<bool Align> | |
| void * | ei_conditional_aligned_malloc (size_t size) |
| template<bool Align> | |
| void * | ei_conditional_aligned_realloc (void *ptr, size_t new_size, size_t old_size) |
| template<typename T > | |
| T | ei_conj (const T &x) |
| template<typename T > | |
| T | ei_cos (const T &x) |
| template<typename T > | |
| T | ei_exp (const T &x) |
| void | ei_handmade_aligned_free (void *ptr) |
| void * | ei_handmade_aligned_malloc (size_t size) |
| template<typename T > | |
| NumTraits< T >::Real | ei_imag (const T &x) |
| template<typename Scalar > | |
| bool | ei_isApprox (const Scalar &x, const Scalar &y, typename NumTraits< Scalar >::Real precision=NumTraits< Scalar >::dummy_precision()) |
| template<typename Scalar > | |
| bool | ei_isApproxOrLessThan (const Scalar &x, const Scalar &y, typename NumTraits< Scalar >::Real precision=NumTraits< Scalar >::dummy_precision()) |
| template<typename Scalar , typename OtherScalar > | |
| bool | ei_isMuchSmallerThan (const Scalar &x, const OtherScalar &y, typename NumTraits< Scalar >::Real precision=NumTraits< Scalar >::dummy_precision()) |
| template<typename T > | |
| T | ei_log (const T &x) |
| template<typename T > | |
| T | ei_pow (const T &x, const T &y) |
| template<typename Scalar > | |
| Quaternion< Scalar > | ei_quaternion_product (const Quaternion< Scalar > &a, const Quaternion< Scalar > &b) |
| template<typename T > | |
| T | ei_random () |
| template<typename T > | |
| T | ei_random (const T &x, const T &y) |
| template<typename T > | |
| NumTraits< T >::Real | ei_real (const T &x) |
| template<typename T > | |
| T | ei_sin (const T &x) |
| template<typename T > | |
| T | ei_sqrt (const T &x) |
| template<typename Scalar , int Dim> | |
| static Matrix< Scalar, 2, 2 > | ei_toRotationMatrix (const Scalar &s) |
| template<typename Scalar , int Dim, typename OtherDerived > | |
| static Matrix< Scalar, Dim, Dim > | ei_toRotationMatrix (const RotationBase< OtherDerived, Dim > &r) |
| template<typename Scalar , int Dim, typename OtherDerived > | |
| static const MatrixBase < OtherDerived > & | ei_toRotationMatrix (const MatrixBase< OtherDerived > &mat) |
| EIGEN_AUTODIFF_DECLARE_GLOBAL_UNARY (tan, using std::tan;using std::cos;return ReturnType(tan(x.value()), x.derivatives()*(Scalar(1)/numext::abs2(cos(x.value()))));) EIGEN_AUTODIFF_DECLARE_GLOBAL_UNARY(asin | |
| EIGEN_AUTODIFF_DECLARE_GLOBAL_UNARY (acos, using std::sqrt;using std::acos;return ReturnType(acos(x.value()), x.derivatives()*(Scalar(-1)/sqrt(1-numext::abs2(x.value()))));) template< typename DerType > struct NumTraits< AutoDiffScalar< DerType > > | |
| template<typename OtherDerived > | |
| EIGEN_STRONG_INLINE const | EIGEN_CWISE_BINOP_RETURN_TYPE (internal::scalar_quotient_op) Cwise< ExpressionType > |
| template<typename OtherDerived > | |
| const | EIGEN_CWISE_BINOP_RETURN_TYPE (std::less) Cwise< ExpressionType > |
| template<typename OtherDerived > | |
| const | EIGEN_CWISE_BINOP_RETURN_TYPE (std::less_equal) Cwise< ExpressionType > |
| template<typename OtherDerived > | |
| const | EIGEN_CWISE_BINOP_RETURN_TYPE (std::greater) Cwise< ExpressionType > |
| template<typename OtherDerived > | |
| const | EIGEN_CWISE_BINOP_RETURN_TYPE (std::greater_equal) Cwise< ExpressionType > |
| template<typename OtherDerived > | |
| const | EIGEN_CWISE_BINOP_RETURN_TYPE (std::equal_to) Cwise< ExpressionType > |
| template<typename OtherDerived > | |
| const | EIGEN_CWISE_BINOP_RETURN_TYPE (std::not_equal_to) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE (std::less) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE (std::less_equal) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE (std::greater) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE (std::greater_equal) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE (std::equal_to) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE (std::not_equal_to) Cwise< ExpressionType > |
| template<typename OtherDerived > | |
| EIGEN_STRONG_INLINE const | EIGEN_CWISE_PRODUCT_RETURN_TYPE (ExpressionType, OtherDerived) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| EIGEN_STRONG_INLINE const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_abs_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| EIGEN_STRONG_INLINE const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_abs2_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_exp_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_log_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_sqrt_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_cos_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_sin_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_pow_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_inverse_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_square_op) Cwise< ExpressionType > |
| template<typename ExpressionType > | |
| const | EIGEN_CWISE_UNOP_RETURN_TYPE (internal::scalar_cube_op) Cwise< ExpressionType > |
| template<typename VectorType , typename HyperplaneType > | |
| void | fitHyperplane (int numPoints, VectorType **points, HyperplaneType *result, typename NumTraits< typename VectorType::Scalar >::Real *soundness=0) |
| bool | getMarketHeader (const std::string &filename, int &sym, bool &iscomplex, bool &isvector) |
| template<typename VectorsType , typename CoeffsType > | |
| HouseholderSequence < VectorsType, CoeffsType > | householderSequence (const VectorsType &v, const CoeffsType &h) |
| Convenience function for constructing a Householder sequence. | |
| template<typename DerType > | |
| DerType::Scalar | imag (const AutoDiffScalar< DerType > &) |
| void | initParallel () |
| template<typename KnotVectorType > | |
| void | KnotAveraging (const KnotVectorType ¶meters, DenseIndex degree, KnotVectorType &knots) |
| Computes knot averages.The knots are computed as
where | |
| template<typename A , typename B > | |
| KroneckerProduct< A, B > | kroneckerProduct (const MatrixBase< A > &a, const MatrixBase< B > &b) |
| template<typename A , typename B > | |
| KroneckerProductSparse< A, B > | kroneckerProduct (const EigenBase< A > &a, const EigenBase< B > &b) |
| std::ptrdiff_t | l1CacheSize () |
| std::ptrdiff_t | l2CacheSize () |
| template<typename VectorType > | |
| void | linearRegression (int numPoints, VectorType **points, VectorType *result, int funcOfOthers) |
| template<typename SparseMatrixType > | |
| bool | loadMarket (SparseMatrixType &mat, const std::string &filename) |
| template<typename VectorType > | |
| bool | loadMarketVector (VectorType &vec, const std::string &filename) |
| template<typename T > | |
| T | machine_epsilon () |
| int | nbThreads () |
| template<typename SparseDerived , typename PermDerived > | |
| const internal::permut_sparsematrix_product_retval < PermutationBase< PermDerived > , SparseDerived, OnTheRight, false > | operator* (const SparseMatrixBase< SparseDerived > &matrix, const PermutationBase< PermDerived > &perm) |
| template<typename SparseDerived , typename PermDerived > | |
| const internal::permut_sparsematrix_product_retval < PermutationBase< PermDerived > , SparseDerived, OnTheLeft, false > | operator* (const PermutationBase< PermDerived > &perm, const SparseMatrixBase< SparseDerived > &matrix) |
| template<typename SparseDerived , typename PermDerived > | |
| const internal::permut_sparsematrix_product_retval < PermutationBase< PermDerived > , SparseDerived, OnTheRight, true > | operator* (const SparseMatrixBase< SparseDerived > &matrix, const Transpose< PermutationBase< PermDerived > > &tperm) |
| template<typename SparseDerived , typename PermDerived > | |
| const internal::permut_sparsematrix_product_retval < PermutationBase< PermDerived > , SparseDerived, OnTheLeft, true > | operator* (const Transpose< PermutationBase< PermDerived > > &tperm, const SparseMatrixBase< SparseDerived > &matrix) |
| template<typename Derived , typename Lhs , typename Rhs > | |
| const ScaledProduct< Derived > | operator* (const ProductBase< Derived, Lhs, Rhs > &prod, const typename Derived::Scalar &x) |
| template<typename Derived , typename Lhs , typename Rhs > | |
| internal::enable_if <!internal::is_same< typename Derived::Scalar, typename Derived::RealScalar >::value, const ScaledProduct< Derived > >::type | operator* (const ProductBase< Derived, Lhs, Rhs > &prod, const typename Derived::RealScalar &x) |
| template<typename Derived , typename Lhs , typename Rhs > | |
| const ScaledProduct< Derived > | operator* (const typename Derived::Scalar &x, const ProductBase< Derived, Lhs, Rhs > &prod) |
| template<typename Derived , typename Lhs , typename Rhs > | |
| internal::enable_if <!internal::is_same< typename Derived::Scalar, typename Derived::RealScalar >::value, const ScaledProduct< Derived > >::type | operator* (const typename Derived::RealScalar &x, const ProductBase< Derived, Lhs, Rhs > &prod) |
| template<typename Derived , typename TranspositionsDerived > | |
| const internal::transposition_matrix_product_retval < TranspositionsDerived, Derived, OnTheRight > | operator* (const MatrixBase< Derived > &matrix, const TranspositionsBase< TranspositionsDerived > &transpositions) |
| template<typename Derived , typename TranspositionDerived > | |
| const internal::transposition_matrix_product_retval < TranspositionDerived, Derived, OnTheLeft > | operator* (const TranspositionsBase< TranspositionDerived > &transpositions, const MatrixBase< Derived > &matrix) |
| template<typename OtherDerived , typename VectorsType , typename CoeffsType , int Side> | |
| internal::matrix_type_times_scalar_type < typename VectorsType::Scalar, OtherDerived >::Type | operator* (const MatrixBase< OtherDerived > &other, const HouseholderSequence< VectorsType, CoeffsType, Side > &h) |
| Computes the product of a matrix with a Householder sequence. | |
| template<typename Derived , typename PermutationDerived > | |
| const internal::permut_matrix_product_retval < PermutationDerived, Derived, OnTheRight > | operator* (const MatrixBase< Derived > &matrix, const PermutationBase< PermutationDerived > &permutation) |
| template<typename Derived , typename PermutationDerived > | |
| const internal::permut_matrix_product_retval < PermutationDerived, Derived, OnTheLeft > | operator* (const PermutationBase< PermutationDerived > &permutation, const MatrixBase< Derived > &matrix) |
| template<typename Derived > | |
| const Eigen::CwiseUnaryOp < Eigen::internal::scalar_inverse_mult_op < typename Derived::Scalar > , const Derived > | operator/ (const typename Derived::Scalar &s, const Eigen::ArrayBase< Derived > &a) |
| Component-wise division of a scalar by array elements. | |
| template<typename Polynomials , typename T > | |
| T | poly_eval (const Polynomials &poly, const T &x) |
| template<typename Polynomials , typename T > | |
| T | poly_eval_horner (const Polynomials &poly, const T &x) |
| template<typename Derived > | |
| const Eigen::CwiseUnaryOp < Eigen::internal::scalar_pow_op < typename Derived::Scalar > , const Derived > | pow (const Eigen::ArrayBase< Derived > &x, const typename Derived::Scalar &exponent) |
| template<typename Derived > | |
| const Eigen::CwiseBinaryOp < Eigen::internal::scalar_binary_pow_op < typename Derived::Scalar, typename Derived::Scalar > , const Derived, const Derived > | pow (const Eigen::ArrayBase< Derived > &x, const Eigen::ArrayBase< Derived > &exponents) |
| const DerType | pow (const Eigen::AutoDiffScalar< DerType > &x, typename Eigen::internal::traits< DerType >::Scalar y) |
| template<typename T > | |
| T | precision () |
| template<typename DerType > | |
| const AutoDiffScalar< DerType > & | real (const AutoDiffScalar< DerType > &x) |
| return | ReturnType (asin(x.value()), x.derivatives()*(Scalar(1)/sqrt(1-numext::abs2(x.value())))) |
| template<typename VectorsType , typename CoeffsType > | |
| HouseholderSequence < VectorsType, CoeffsType, OnTheRight > | rightHouseholderSequence (const VectorsType &v, const CoeffsType &h) |
| Convenience function for constructing a Householder sequence. | |
| template<typename RootVector , typename Polynomial > | |
| void | roots_to_monicPolynomial (const RootVector &rv, Polynomial &poly) |
| template<typename SparseMatrixType > | |
| bool | saveMarket (const SparseMatrixType &mat, const std::string &filename, int sym=0) |
| template<typename VectorType > | |
| bool | saveMarketVector (const VectorType &vec, const std::string &filename) |
| static UniformScaling< float > | Scaling (float s) |
| static UniformScaling< double > | Scaling (double s) |
| template<typename RealScalar > | |
| static UniformScaling < std::complex< RealScalar > > | Scaling (const std::complex< RealScalar > &s) |
| template<typename Scalar > | |
| static DiagonalMatrix< Scalar, 2 > | Scaling (const Scalar &sx, const Scalar &sy) |
| template<typename Scalar > | |
| static DiagonalMatrix< Scalar, 3 > | Scaling (const Scalar &sx, const Scalar &sy, const Scalar &sz) |
| template<typename Derived > | |
| static const DiagonalWrapper < const Derived > | Scaling (const MatrixBase< Derived > &coeffs) |
| void | setCpuCacheSizes (std::ptrdiff_t l1, std::ptrdiff_t l2) |
| void | setNbThreads (int v) |
| void | ssaupd_ (int *ido, char *bmat, int *n, char *which, int *nev, float *tol, float *resid, int *ncv, float *v, int *ldv, int *iparam, int *ipntr, float *workd, float *workl, int *lworkl, int *info) |
| void | sseupd_ (int *rvec, char *All, int *select, float *d, float *z, int *ldz, float *sigma, char *bmat, int *n, char *which, int *nev, float *tol, float *resid, int *ncv, float *v, int *ldv, int *iparam, int *ipntr, float *workd, float *workl, int *lworkl, int *ierr) |
| template<typename Derived , typename OtherDerived > | |
| internal::umeyama_transform_matrix_type < Derived, OtherDerived > ::type | umeyama (const MatrixBase< Derived > &src, const MatrixBase< OtherDerived > &dst, bool with_scaling=true) |
| Returns the transformation between two point sets. | |
| void | umfpack_free_numeric (void **Numeric, double) |
| void | umfpack_free_numeric (void **Numeric, std::complex< double >) |
| void | umfpack_free_symbolic (void **Symbolic, double) |
| void | umfpack_free_symbolic (void **Symbolic, std::complex< double >) |
| int | umfpack_get_determinant (double *Mx, double *Ex, void *NumericHandle, double User_Info[UMFPACK_INFO]) |
| int | umfpack_get_determinant (std::complex< double > *Mx, double *Ex, void *NumericHandle, double User_Info[UMFPACK_INFO]) |
| int | umfpack_get_lunz (int *lnz, int *unz, int *n_row, int *n_col, int *nz_udiag, void *Numeric, double) |
| int | umfpack_get_lunz (int *lnz, int *unz, int *n_row, int *n_col, int *nz_udiag, void *Numeric, std::complex< double >) |
| int | umfpack_get_numeric (int Lp[], int Lj[], double Lx[], int Up[], int Ui[], double Ux[], int P[], int Q[], double Dx[], int *do_recip, double Rs[], void *Numeric) |
| int | umfpack_get_numeric (int Lp[], int Lj[], std::complex< double > Lx[], int Up[], int Ui[], std::complex< double > Ux[], int P[], int Q[], std::complex< double > Dx[], int *do_recip, double Rs[], void *Numeric) |
| int | umfpack_numeric (const int Ap[], const int Ai[], const double Ax[], void *Symbolic, void **Numeric, const double Control[UMFPACK_CONTROL], double Info[UMFPACK_INFO]) |
| int | umfpack_numeric (const int Ap[], const int Ai[], const std::complex< double > Ax[], void *Symbolic, void **Numeric, const double Control[UMFPACK_CONTROL], double Info[UMFPACK_INFO]) |
| int | umfpack_solve (int sys, const int Ap[], const int Ai[], const double Ax[], double X[], const double B[], void *Numeric, const double Control[UMFPACK_CONTROL], double Info[UMFPACK_INFO]) |
| int | umfpack_solve (int sys, const int Ap[], const int Ai[], const std::complex< double > Ax[], std::complex< double > X[], const std::complex< double > B[], void *Numeric, const double Control[UMFPACK_CONTROL], double Info[UMFPACK_INFO]) |
| int | umfpack_symbolic (int n_row, int n_col, const int Ap[], const int Ai[], const double Ax[], void **Symbolic, const double Control[UMFPACK_CONTROL], double Info[UMFPACK_INFO]) |
| int | umfpack_symbolic (int n_row, int n_col, const int Ap[], const int Ai[], const std::complex< double > Ax[], void **Symbolic, const double Control[UMFPACK_CONTROL], double Info[UMFPACK_INFO]) |
| template<typename _Scalar , int _Options, typename _Index > | |
| cholmod_sparse | viewAsCholmod (SparseMatrix< _Scalar, _Options, _Index > &mat) |
| template<typename _Scalar , int _Options, typename _Index > | |
| const cholmod_sparse | viewAsCholmod (const SparseMatrix< _Scalar, _Options, _Index > &mat) |
| template<typename _Scalar , int _Options, typename _Index , unsigned int UpLo> | |
| cholmod_sparse | viewAsCholmod (const SparseSelfAdjointView< SparseMatrix< _Scalar, _Options, _Index >, UpLo > &mat) |
| template<typename Derived > | |
| cholmod_dense | viewAsCholmod (MatrixBase< Derived > &mat) |
| template<typename Scalar , int Flags, typename Index > | |
| MappedSparseMatrix< Scalar, Flags, Index > | viewAsEigen (cholmod_sparse &cm) |
Variables | |
| const unsigned int | ActualPacketAccessBit = 0x0 |
| const unsigned int | AlignedBit = 0x80 |
| const int | CoherentAccessPattern = 0x1 |
| const unsigned int | DirectAccessBit = 0x40 |
| const int | Dynamic = -1 |
| const int | DynamicIndex = 0xffffff |
| const unsigned int | EvalBeforeAssigningBit = 0x4 |
| const unsigned int | EvalBeforeNestingBit = 0x2 |
| const unsigned int | HereditaryBits |
| const int | Infinity = -1 |
| const int | InnerRandomAccessPattern = 0x2 | CoherentAccessPattern |
| const unsigned int | LinearAccessBit = 0x10 |
| const unsigned int | LowerTriangular = Lower |
| const unsigned int | LowerTriangularBit = Lower |
| const unsigned int | LvalueBit = 0x20 |
| const unsigned int | NestByRefBit = 0x100 |
| const int | OuterRandomAccessPattern = 0x4 | CoherentAccessPattern |
| const unsigned int | PacketAccessBit = 0x8 |
| const int | RandomAccessPattern = 0x8 | OuterRandomAccessPattern | InnerRandomAccessPattern |
| const unsigned int | RowMajorBit = 0x1 |
| const unsigned int | SelfAdjointBit = SelfAdjoint |
| const unsigned int | SkylineBit = 0x1200 |
| const unsigned int | UnitDiagBit = UnitDiag |
| const unsigned int | UnitLowerTriangular = UnitLower |
| const unsigned int | UnitUpperTriangular = UnitUpper |
| const unsigned int | UpperTriangular = Upper |
| const unsigned int | UpperTriangularBit = Upper |
Detailed Description
iterative scaling algorithm to equilibrate rows and column norms in matrices
This class can be used as a preprocessing tool to accelerate the convergence of iterative methods
This feature is useful to limit the pivoting amount during LU/ILU factorization The scaling strategy as presented here preserves the symmetry of the problem NOTE It is assumed that the matrix does not have empty row or column,
Example with key steps
VectorXd x(n), b(n); SparseMatrix<double> A; // fill A and b; IterScaling<SparseMatrix<double> > scal; // Compute the left and right scaling vectors. The matrix is equilibrated at output scal.computeRef(A); // Scale the right hand side b = scal.LeftScaling().cwiseProduct(b); // Now, solve the equilibrated linear system with any available solver // Scale back the computed solution x = scal.RightScaling().cwiseProduct(x);
- Template Parameters:
-
_MatrixType the type of the matrix. It should be a real square sparsematrix
References : D. Ruiz and B. Ucar, A Symmetry Preserving Algorithm for Matrix Scaling, INRIA Research report RR-7552
- See also:
- IncompleteLUT
Typedef Documentation
Definition at line 27 of file XprHelper.h.
| typedef Spline<double,2> Eigen::Spline2d |
2D double B-spline with dynamic degree.
Definition at line 80 of file SplineFwd.h.
| typedef Spline<float,2> Eigen::Spline2f |
2D float B-spline with dynamic degree.
Definition at line 74 of file SplineFwd.h.
| typedef Spline<double,3> Eigen::Spline3d |
3D double B-spline with dynamic degree.
Definition at line 83 of file SplineFwd.h.
| typedef Spline<float,3> Eigen::Spline3f |
3D float B-spline with dynamic degree.
Definition at line 77 of file SplineFwd.h.
Enumeration Type Documentation
| anonymous enum |
Definition at line 38 of file GeneralProduct.h.
| anonymous enum |
- Enumerator:
DefaultTraversal LinearTraversal InnerVectorizedTraversal LinearVectorizedTraversal SliceVectorizedTraversal InvalidTraversal AllAtOnceTraversal
Definition at line 220 of file Constants.h.
| anonymous enum |
Definition at line 242 of file Constants.h.
| anonymous enum |
Definition at line 254 of file Constants.h.
| anonymous enum |
Definition at line 300 of file Constants.h.
| anonymous enum |
- Enumerator:
CoeffBasedProductMode LazyCoeffBasedProductMode OuterProduct InnerProduct GemvProduct GemmProduct
Definition at line 421 of file Constants.h.
| anonymous enum |
Definition at line 24 of file SkylineUtil.h.
| anonymous enum |
Definition at line 16 of file MatrixMarketIterator.h.
| enum Eigen::Action |
Definition at line 425 of file Constants.h.
Definition at line 23 of file SkylineUtil.h.
| enum Eigen::CholmodMode |
Definition at line 149 of file CholmodSupport.h.
| enum Eigen::Default_t |
Definition at line 296 of file Constants.h.
| enum Eigen::NoChange_t |
Definition at line 294 of file Constants.h.
Definition at line 18 of file NumericalDiff.h.
| enum Eigen::Sequential_t |
Definition at line 295 of file Constants.h.
Definition at line 15 of file SimplicialCholesky.h.
Function Documentation
| const AutoDiffScalar<Matrix<typename internal::traits<DerTypeA>::Scalar,Dynamic,1> > Eigen::atan2 | ( | const AutoDiffScalar< DerTypeA > & | a, |
| const AutoDiffScalar< DerTypeB > & | b | ||
| ) | [inline] |
Definition at line 593 of file AutoDiffScalar.h.
| T Eigen::AutoDiffScalar< DerType > | ( | min | ) | const [inline] |
| T Eigen::AutoDiffScalar< DerType > | ( | max | ) | const [inline] |
| void Eigen::basisFunctionDerivativesImpl | ( | const SplineType & | spline, |
| typename SplineType::Scalar | u, | ||
| DenseIndex | order, | ||
| DerivativeType & | N_ | ||
| ) |
| AlignedBox<Scalar, Dim> Eigen::bounding_box | ( | const Matrix< Scalar, Dim, 1 > & | v | ) |
| void Eigen::BVIntersect | ( | const BVH & | tree, |
| Intersector & | intersector | ||
| ) |
Given a BVH, runs the query encapsulated by intersector. The Intersector type must provide the following members:
bool intersectVolume(const BVH::Volume &volume) //returns true if volume intersects the query bool intersectObject(const BVH::Object &object) //returns true if the search should terminate immediately
Definition at line 79 of file BVAlgorithms.h.
| void Eigen::BVIntersect | ( | const BVH1 & | tree1, |
| const BVH2 & | tree2, | ||
| Intersector & | intersector | ||
| ) |
Given two BVH's, runs the query on their Cartesian product encapsulated by intersector. The Intersector type must provide the following members:
bool intersectVolumeVolume(const BVH1::Volume &v1, const BVH2::Volume &v2) //returns true if product of volumes intersects the query bool intersectVolumeObject(const BVH1::Volume &v1, const BVH2::Object &o2) //returns true if the volume-object product intersects the query bool intersectObjectVolume(const BVH1::Object &o1, const BVH2::Volume &v2) //returns true if the volume-object product intersects the query bool intersectObjectObject(const BVH1::Object &o1, const BVH2::Object &o2) //returns true if the search should terminate immediately
Definition at line 93 of file BVAlgorithms.h.
| Minimizer::Scalar Eigen::BVMinimize | ( | const BVH & | tree, |
| Minimizer & | minimizer | ||
| ) |
Given a BVH, runs the query encapsulated by minimizer.
- Returns:
- the minimum value. The Minimizer type must provide the following members:
typedef Scalar //the numeric type of what is being minimized--not necessarily the Scalar type of the BVH (if it has one) Scalar minimumOnVolume(const BVH::Volume &volume) Scalar minimumOnObject(const BVH::Object &object)
Definition at line 219 of file BVAlgorithms.h.
| Minimizer::Scalar Eigen::BVMinimize | ( | const BVH1 & | tree1, |
| const BVH2 & | tree2, | ||
| Minimizer & | minimizer | ||
| ) |
Given two BVH's, runs the query on their cartesian product encapsulated by minimizer.
- Returns:
- the minimum value. The Minimizer type must provide the following members:
typedef Scalar //the numeric type of what is being minimized--not necessarily the Scalar type of the BVH (if it has one) Scalar minimumOnVolumeVolume(const BVH1::Volume &v1, const BVH2::Volume &v2) Scalar minimumOnVolumeObject(const BVH1::Volume &v1, const BVH2::Object &o2) Scalar minimumOnObjectVolume(const BVH1::Object &o1, const BVH2::Volume &v2) Scalar minimumOnObjectObject(const BVH1::Object &o1, const BVH2::Object &o2)
Definition at line 235 of file BVAlgorithms.h.
| NumTraits<typename Polynomial::Scalar>::Real Eigen::cauchy_max_bound | ( | const Polynomial & | poly | ) | [inline] |
- Returns:
- a maximum bound for the absolute value of any root of the polynomial.
- Parameters:
-
[in] poly : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 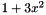 is stored as a vector
is stored as a vector ![$ [ 1, 0, 3 ] $](form_206.png) .
.
Precondition: the leading coefficient of the input polynomial poly must be non zero
Definition at line 75 of file PolynomialUtils.h.
| NumTraits<typename Polynomial::Scalar>::Real Eigen::cauchy_min_bound | ( | const Polynomial & | poly | ) | [inline] |
- Returns:
- a minimum bound for the absolute value of any non zero root of the polynomial.
- Parameters:
-
[in] poly : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 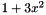 is stored as a vector
is stored as a vector ![$ [ 1, 0, 3 ] $](form_206.png) .
.
Definition at line 98 of file PolynomialUtils.h.
| std::complex<Scalar> Eigen::cdiv | ( | const Scalar & | xr, |
| const Scalar & | xi, | ||
| const Scalar & | yr, | ||
| const Scalar & | yi | ||
| ) |
Definition at line 422 of file EigenSolver.h.
| void Eigen::ChordLengths | ( | const PointArrayType & | pts, |
| KnotVectorType & | chord_lengths | ||
| ) |
Computes chord length parameters which are required for spline interpolation.
- Parameters:
-
[in] pts The data points to which a spline should be fit. [out] chord_lengths The resulting chord lenggth vector.
- See also:
- Les Piegl and Wayne Tiller, The NURBS book (2nd ed.), 1997, 9.2.1 Global Curve Interpolation to Point Data
Definition at line 62 of file SplineFitting.h.
| const AutoDiffScalar<DerType>& Eigen::conj | ( | const AutoDiffScalar< DerType > & | x | ) | [inline] |
Definition at line 533 of file AutoDiffScalar.h.
| void Eigen::derivativesImpl | ( | const SplineType & | spline, |
| typename SplineType::Scalar | u, | ||
| DenseIndex | order, | ||
| DerivativeType & | der | ||
| ) |
| void Eigen::dsaupd_ | ( | int * | ido, |
| char * | bmat, | ||
| int * | n, | ||
| char * | which, | ||
| int * | nev, | ||
| double * | tol, | ||
| double * | resid, | ||
| int * | ncv, | ||
| double * | v, | ||
| int * | ldv, | ||
| int * | iparam, | ||
| int * | ipntr, | ||
| double * | workd, | ||
| double * | workl, | ||
| int * | lworkl, | ||
| int * | info | ||
| ) |
| void Eigen::dseupd_ | ( | int * | rvec, |
| char * | All, | ||
| int * | select, | ||
| double * | d, | ||
| double * | z, | ||
| int * | ldz, | ||
| double * | sigma, | ||
| char * | bmat, | ||
| int * | n, | ||
| char * | which, | ||
| int * | nev, | ||
| double * | tol, | ||
| double * | resid, | ||
| int * | ncv, | ||
| double * | v, | ||
| int * | ldv, | ||
| int * | iparam, | ||
| int * | ipntr, | ||
| double * | workd, | ||
| double * | workl, | ||
| int * | lworkl, | ||
| int * | ierr | ||
| ) |
| NumTraits<T>::Real Eigen::ei_abs | ( | const T & | x | ) | [inline] |
Definition at line 18 of file Eigen/src/Eigen2Support/MathFunctions.h.
| NumTraits<T>::Real Eigen::ei_abs2 | ( | const T & | x | ) | [inline] |
Definition at line 19 of file Eigen/src/Eigen2Support/MathFunctions.h.
| void Eigen::ei_aligned_delete | ( | T * | ptr, |
| size_t | size | ||
| ) | [inline] |
Definition at line 38 of file Eigen2Support/Memory.h.
| void Eigen::ei_aligned_free | ( | void * | ptr | ) | [inline] |
Definition at line 16 of file Eigen2Support/Memory.h.
| void* Eigen::ei_aligned_malloc | ( | size_t | size | ) | [inline] |
Definition at line 15 of file Eigen2Support/Memory.h.
| T* Eigen::ei_aligned_new | ( | size_t | size | ) | [inline] |
Definition at line 34 of file Eigen2Support/Memory.h.
| void* Eigen::ei_aligned_realloc | ( | void * | ptr, |
| size_t | new_size, | ||
| size_t | old_size | ||
| ) | [inline] |
Definition at line 17 of file Eigen2Support/Memory.h.
| T Eigen::ei_atan2 | ( | const T & | x, |
| const T & | y | ||
| ) | [inline] |
Definition at line 25 of file Eigen/src/Eigen2Support/MathFunctions.h.
| void Eigen::ei_conditional_aligned_free | ( | void * | ptr | ) | [inline] |
Definition at line 25 of file Eigen2Support/Memory.h.
| void* Eigen::ei_conditional_aligned_malloc | ( | size_t | size | ) | [inline] |
Definition at line 21 of file Eigen2Support/Memory.h.
| void* Eigen::ei_conditional_aligned_realloc | ( | void * | ptr, |
| size_t | new_size, | ||
| size_t | old_size | ||
| ) | [inline] |
Definition at line 29 of file Eigen2Support/Memory.h.
| T Eigen::ei_conj | ( | const T & | x | ) | [inline] |
Definition at line 17 of file Eigen/src/Eigen2Support/MathFunctions.h.
| T Eigen::ei_cos | ( | const T & | x | ) | [inline] |
Definition at line 24 of file Eigen/src/Eigen2Support/MathFunctions.h.
| T Eigen::ei_exp | ( | const T & | x | ) | [inline] |
Definition at line 21 of file Eigen/src/Eigen2Support/MathFunctions.h.
| void Eigen::ei_handmade_aligned_free | ( | void * | ptr | ) | [inline] |
Definition at line 19 of file Eigen2Support/Memory.h.
| void* Eigen::ei_handmade_aligned_malloc | ( | size_t | size | ) | [inline] |
Definition at line 18 of file Eigen2Support/Memory.h.
| NumTraits<T>::Real Eigen::ei_imag | ( | const T & | x | ) | [inline] |
Definition at line 16 of file Eigen/src/Eigen2Support/MathFunctions.h.
| bool Eigen::ei_isApprox | ( | const Scalar & | x, |
| const Scalar & | y, | ||
| typename NumTraits< Scalar >::Real | precision = NumTraits<Scalar>::dummy_precision() |
||
| ) | [inline] |
Definition at line 42 of file Eigen/src/Eigen2Support/MathFunctions.h.
| bool Eigen::ei_isApproxOrLessThan | ( | const Scalar & | x, |
| const Scalar & | y, | ||
| typename NumTraits< Scalar >::Real | precision = NumTraits<Scalar>::dummy_precision() |
||
| ) | [inline] |
Definition at line 49 of file Eigen/src/Eigen2Support/MathFunctions.h.
| bool Eigen::ei_isMuchSmallerThan | ( | const Scalar & | x, |
| const OtherScalar & | y, | ||
| typename NumTraits< Scalar >::Real | precision = NumTraits<Scalar>::dummy_precision() |
||
| ) | [inline] |
Definition at line 35 of file Eigen/src/Eigen2Support/MathFunctions.h.
| T Eigen::ei_log | ( | const T & | x | ) | [inline] |
Definition at line 22 of file Eigen/src/Eigen2Support/MathFunctions.h.
| T Eigen::ei_pow | ( | const T & | x, |
| const T & | y | ||
| ) | [inline] |
Definition at line 26 of file Eigen/src/Eigen2Support/MathFunctions.h.
| Quaternion<Scalar> Eigen::ei_quaternion_product | ( | const Quaternion< Scalar > & | a, |
| const Quaternion< Scalar > & | b | ||
| ) | [inline] |
Definition at line 215 of file Eigen2Support/Geometry/Quaternion.h.
| T Eigen::ei_random | ( | ) | [inline] |
Definition at line 27 of file Eigen/src/Eigen2Support/MathFunctions.h.
| T Eigen::ei_random | ( | const T & | x, |
| const T & | y | ||
| ) | [inline] |
Definition at line 28 of file Eigen/src/Eigen2Support/MathFunctions.h.
| NumTraits<T>::Real Eigen::ei_real | ( | const T & | x | ) | [inline] |
Definition at line 15 of file Eigen/src/Eigen2Support/MathFunctions.h.
| T Eigen::ei_sin | ( | const T & | x | ) | [inline] |
Definition at line 23 of file Eigen/src/Eigen2Support/MathFunctions.h.
| T Eigen::ei_sqrt | ( | const T & | x | ) | [inline] |
Definition at line 20 of file Eigen/src/Eigen2Support/MathFunctions.h.
| static Matrix<Scalar,2,2> Eigen::ei_toRotationMatrix | ( | const Scalar & | s | ) | [inline, static] |
Definition at line 103 of file Eigen2Support/Geometry/RotationBase.h.
| static Matrix<Scalar,Dim,Dim> Eigen::ei_toRotationMatrix | ( | const RotationBase< OtherDerived, Dim > & | r | ) | [inline, static] |
Definition at line 110 of file Eigen2Support/Geometry/RotationBase.h.
| static const MatrixBase<OtherDerived>& Eigen::ei_toRotationMatrix | ( | const MatrixBase< OtherDerived > & | mat | ) | [inline, static] |
Definition at line 116 of file Eigen2Support/Geometry/RotationBase.h.
| Eigen::EIGEN_AUTODIFF_DECLARE_GLOBAL_UNARY | ( | tan | , |
| using std::tan;using std::cos;return ReturnType(tan(x.value()), x.derivatives()*(Scalar(1)/numext::abs2(cos(x.value())))); | |||
| ) |
| Eigen::EIGEN_AUTODIFF_DECLARE_GLOBAL_UNARY | ( | acos | , |
| using std::sqrt;using std::acos;return ReturnType(acos(x.value()), x.derivatives()*(Scalar(-1)/sqrt(1-numext::abs2(x.value())))); | |||
| ) |
Definition at line 622 of file AutoDiffScalar.h.
| EIGEN_STRONG_INLINE const Eigen::EIGEN_CWISE_BINOP_RETURN_TYPE | ( | internal::scalar_quotient_op | ) |
Definition at line 64 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_BINOP_RETURN_TYPE | ( | std::less | ) | [inline] |
- Deprecated:
- ArrayBase::operator<()
Definition at line 157 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_BINOP_RETURN_TYPE | ( | std::less_equal | ) | [inline] |
- Deprecated:
- ArrayBase::<=()
Definition at line 166 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_BINOP_RETURN_TYPE | ( | std::greater | ) | [inline] |
Definition at line 175 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_BINOP_RETURN_TYPE | ( | std::greater_equal | ) | [inline] |
- Deprecated:
- ArrayBase::operator>=()
Definition at line 184 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_BINOP_RETURN_TYPE | ( | std::equal_to | ) | [inline] |
Definition at line 193 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_BINOP_RETURN_TYPE | ( | std::not_equal_to | ) | [inline] |
- Deprecated:
- ArrayBase::operator!=()
Definition at line 202 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE | ( | std::less | ) | [inline] |
- Deprecated:
- ArrayBase::operator<(Scalar)
Definition at line 212 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE | ( | std::less_equal | ) | [inline] |
- Deprecated:
- ArrayBase::operator<=(Scalar)
Definition at line 221 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE | ( | std::greater | ) | [inline] |
- Deprecated:
- ArrayBase::operator>(Scalar)
Definition at line 230 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE | ( | std::greater_equal | ) | [inline] |
- Deprecated:
- ArrayBase::operator>=(Scalar)
Definition at line 239 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE | ( | std::equal_to | ) | [inline] |
- Deprecated:
- ArrayBase::operator==(Scalar)
Definition at line 248 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_COMP_TO_SCALAR_RETURN_TYPE | ( | std::not_equal_to | ) | [inline] |
- Deprecated:
- ArrayBase::operator!=(Scalar)
Definition at line 257 of file CwiseOperators.h.
| EIGEN_STRONG_INLINE const Eigen::EIGEN_CWISE_PRODUCT_RETURN_TYPE | ( | ExpressionType | , |
| OtherDerived | |||
| ) |
Definition at line 55 of file CwiseOperators.h.
| EIGEN_STRONG_INLINE const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_abs_op | ) |
Definition at line 22 of file CwiseOperators.h.
| EIGEN_STRONG_INLINE const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_abs2_op | ) |
Definition at line 30 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_exp_op | ) | [inline] |
Definition at line 38 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_log_op | ) | [inline] |
Definition at line 46 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_sqrt_op | ) | [inline] |
Definition at line 94 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_cos_op | ) | [inline] |
Definition at line 102 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_sin_op | ) | [inline] |
Definition at line 111 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_pow_op | ) | [inline] |
Definition at line 120 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_inverse_op | ) | [inline] |
Definition at line 129 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_square_op | ) | [inline] |
Definition at line 137 of file CwiseOperators.h.
| const Eigen::EIGEN_CWISE_UNOP_RETURN_TYPE | ( | internal::scalar_cube_op | ) | [inline] |
Definition at line 145 of file CwiseOperators.h.
| void Eigen::fitHyperplane | ( | int | numPoints, |
| VectorType ** | points, | ||
| HyperplaneType * | result, | ||
| typename NumTraits< typename VectorType::Scalar >::Real * | soundness = 0 |
||
| ) |
This function is quite similar to linearRegression(), so we refer to the documentation of this function and only list here the differences.
The main difference from linearRegression() is that this function doesn't take a funcOfOthers argument. Instead, it finds a general equation of the form
![\[ r_0 x_0 + \cdots + r_{n-1}x_{n-1} + r_n = 0, \]](form_64.png)
where  ,
, ![$r_i=retCoefficients[i]$](form_65.png) , and we denote by
, and we denote by  the n coordinates in the n-dimensional space.
the n coordinates in the n-dimensional space.
Thus, the vector retCoefficients has size 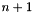 , which is another difference from linearRegression().
, which is another difference from linearRegression().
In practice, this function performs an hyper-plane fit in a total least square sense via the following steps: 1 - center the data to the mean 2 - compute the covariance matrix 3 - pick the eigenvector corresponding to the smallest eigenvalue of the covariance matrix The ratio of the smallest eigenvalue and the second one gives us a hint about the relevance of the solution. This value is optionally returned in soundness.
- See also:
- linearRegression()
Definition at line 130 of file LeastSquares.h.
| bool Eigen::getMarketHeader | ( | const std::string & | filename, |
| int & | sym, | ||
| bool & | iscomplex, | ||
| bool & | isvector | ||
| ) | [inline] |
Definition at line 109 of file MarketIO.h.
| HouseholderSequence<VectorsType,CoeffsType> Eigen::householderSequence | ( | const VectorsType & | v, |
| const CoeffsType & | h | ||
| ) |
Convenience function for constructing a Householder sequence.
\
- Returns:
- A HouseholderSequence constructed from the specified arguments.
Definition at line 422 of file HouseholderSequence.h.
| DerType::Scalar Eigen::imag | ( | const AutoDiffScalar< DerType > & | ) | [inline] |
Definition at line 537 of file AutoDiffScalar.h.
| void Eigen::initParallel | ( | ) | [inline] |
Must be call first when calling Eigen from multiple threads
Definition at line 48 of file Parallelizer.h.
| void Eigen::KnotAveraging | ( | const KnotVectorType & | parameters, |
| DenseIndex | degree, | ||
| KnotVectorType & | knots | ||
| ) |
Computes knot averages.The knots are computed as
where  is the degree and
is the degree and  the number knots of the desired interpolating spline.
the number knots of the desired interpolating spline.
- Parameters:
-
[in] parameters The input parameters. During interpolation one for each data point. [in] degree The spline degree which is used during the interpolation. [out] knots The output knot vector.
- See also:
- Les Piegl and Wayne Tiller, The NURBS book (2nd ed.), 1997, 9.2.1 Global Curve Interpolation to Point Data
Definition at line 41 of file SplineFitting.h.
| KroneckerProduct<A,B> Eigen::kroneckerProduct | ( | const MatrixBase< A > & | a, |
| const MatrixBase< B > & | b | ||
| ) |
Computes Kronecker tensor product of two dense matrices
- Warning:
- If you want to replace a matrix by its Kronecker product with some matrix, do NOT do this: instead, use eval() to work around this:
A = kroneckerProduct(A,B); // bug!!! caused by aliasing effect
A = kroneckerProduct(A,B).eval();
- Returns:
- Kronecker tensor product of a and b
Definition at line 220 of file KroneckerTensorProduct.h.
| KroneckerProductSparse<A,B> Eigen::kroneckerProduct | ( | const EigenBase< A > & | a, |
| const EigenBase< B > & | b | ||
| ) |
Computes Kronecker tensor product of two matrices, at least one of which is sparse
- Parameters:
-
a Dense/sparse matrix a b Dense/sparse matrix b
- Returns:
- Kronecker tensor product of a and b, stored in a sparse matrix
Definition at line 237 of file KroneckerTensorProduct.h.
| std::ptrdiff_t Eigen::l1CacheSize | ( | ) | [inline] |
- Returns:
- the currently set level 1 cpu cache size (in bytes) used to estimate the ideal blocking size parameters.
- See also:
- setCpuCacheSize
Definition at line 1313 of file GeneralBlockPanelKernel.h.
| std::ptrdiff_t Eigen::l2CacheSize | ( | ) | [inline] |
- Returns:
- the currently set level 2 cpu cache size (in bytes) used to estimate the ideal blocking size parameters.
- See also:
- setCpuCacheSize
Definition at line 1322 of file GeneralBlockPanelKernel.h.
| void Eigen::linearRegression | ( | int | numPoints, |
| VectorType ** | points, | ||
| VectorType * | result, | ||
| int | funcOfOthers | ||
| ) |
For a set of points, this function tries to express one of the coords as a linear (affine) function of the other coords.
This is best explained by an example. This function works in full generality, for points in a space of arbitrary dimension, and also over the complex numbers, but for this example we will work in dimension 3 over the real numbers (doubles).
So let us work with the following set of 5 points given by their  coordinates:
coordinates:
Vector3d points[5]; points[0] = Vector3d( 3.02, 6.89, -4.32 ); points[1] = Vector3d( 2.01, 5.39, -3.79 ); points[2] = Vector3d( 2.41, 6.01, -4.01 ); points[3] = Vector3d( 2.09, 5.55, -3.86 ); points[4] = Vector3d( 2.58, 6.32, -4.10 );
Suppose that we want to express the second coordinate (  ) as a linear expression in
) as a linear expression in  and
and  , that is,
, that is,
![\[ y=ax+bz+c \]](form_50.png)
for some constants 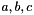 . Thus, we want to find the best possible constants
. Thus, we want to find the best possible constants 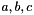 so that the plane of equation
so that the plane of equation 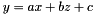 fits best the five above points. To do that, call this function as follows:
fits best the five above points. To do that, call this function as follows:
Vector3d coeffs; // will store the coefficients a, b, c linearRegression( 5, &points, &coeffs, 1 // the coord to express as a function of // the other ones. 0 means x, 1 means y, 2 means z. );
Now the vector coeffs is approximately  . Thus, we get
. Thus, we get 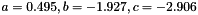 . Let us check for instance how near points[0] is from the plane of equation
. Let us check for instance how near points[0] is from the plane of equation 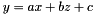 . Looking at the coords of points[0], we see that:
. Looking at the coords of points[0], we see that:
![\[ax+bz+c = 0.495 * 3.02 + (-1.927) * (-4.32) + (-2.906) = 6.91.\]](form_55.png)
On the other hand, we have 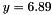 . We see that the values
. We see that the values 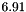 and
and 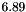 are near, so points[0] is very near the plane of equation
are near, so points[0] is very near the plane of equation 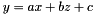 .
.
Let's now describe precisely the parameters:
- Parameters:
-
numPoints the number of points points the array of pointers to the points on which to perform the linear regression result pointer to the vector in which to store the result. This vector must be of the same type and size as the data points. The meaning of its coords is as follows. For brevity, let 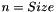 ,
, ![$r_i=result[i]$](form_60.png) , and
, and 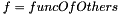 . Denote by
. Denote by 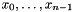 the n coordinates in the n-dimensional space. Then the resulting equation is:
the n coordinates in the n-dimensional space. Then the resulting equation is: ![\[ x_f = r_0 x_0 + \cdots + r_{f-1}x_{f-1} + r_{f+1}x_{f+1} + \cdots + r_{n-1}x_{n-1} + r_n. \]](form_63.png)
funcOfOthers Determines which coord to express as a function of the others. Coords are numbered starting from 0, so that a value of 0 means 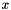 , 1 means
, 1 means 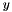 , 2 means
, 2 means 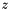 , ...
, ...
- See also:
- fitHyperplane()
Definition at line 85 of file LeastSquares.h.
| bool Eigen::loadMarket | ( | SparseMatrixType & | mat, |
| const std::string & | filename | ||
| ) |
Definition at line 133 of file MarketIO.h.
| bool Eigen::loadMarketVector | ( | VectorType & | vec, |
| const std::string & | filename | ||
| ) |
Definition at line 192 of file MarketIO.h.
| T Eigen::machine_epsilon | ( | ) | [inline] |
Definition at line 31 of file Eigen/src/Eigen2Support/MathFunctions.h.
| int Eigen::nbThreads | ( | ) | [inline] |
- Returns:
- the max number of threads reserved for Eigen
- See also:
- setNbThreads
Definition at line 58 of file Parallelizer.h.
| const internal::permut_sparsematrix_product_retval<PermutationBase<PermDerived>, SparseDerived, OnTheRight, false> Eigen::operator* | ( | const SparseMatrixBase< SparseDerived > & | matrix, |
| const PermutationBase< PermDerived > & | perm | ||
| ) | [inline] |
- Returns:
- the matrix with the permutation applied to the columns
Definition at line 112 of file SparsePermutation.h.
| const internal::permut_sparsematrix_product_retval<PermutationBase<PermDerived>, SparseDerived, OnTheLeft, false> Eigen::operator* | ( | const PermutationBase< PermDerived > & | perm, |
| const SparseMatrixBase< SparseDerived > & | matrix | ||
| ) | [inline] |
- Returns:
- the matrix with the permutation applied to the rows
Definition at line 121 of file SparsePermutation.h.
| const internal::permut_sparsematrix_product_retval<PermutationBase<PermDerived>, SparseDerived, OnTheRight, true> Eigen::operator* | ( | const SparseMatrixBase< SparseDerived > & | matrix, |
| const Transpose< PermutationBase< PermDerived > > & | tperm | ||
| ) | [inline] |
- Returns:
- the matrix with the inverse permutation applied to the columns.
Definition at line 132 of file SparsePermutation.h.
| const internal::permut_sparsematrix_product_retval<PermutationBase<PermDerived>, SparseDerived, OnTheLeft, true> Eigen::operator* | ( | const Transpose< PermutationBase< PermDerived > > & | tperm, |
| const SparseMatrixBase< SparseDerived > & | matrix | ||
| ) | [inline] |
- Returns:
- the matrix with the inverse permutation applied to the rows.
Definition at line 141 of file SparsePermutation.h.
| const ScaledProduct<Derived> Eigen::operator* | ( | const ProductBase< Derived, Lhs, Rhs > & | prod, |
| const typename Derived::Scalar & | x | ||
| ) |
Definition at line 210 of file ProductBase.h.
| internal::enable_if<!internal::is_same<typename Derived::Scalar,typename Derived::RealScalar>::value, const ScaledProduct<Derived> >::type Eigen::operator* | ( | const ProductBase< Derived, Lhs, Rhs > & | prod, |
| const typename Derived::RealScalar & | x | ||
| ) |
Definition at line 216 of file ProductBase.h.
| const ScaledProduct<Derived> Eigen::operator* | ( | const typename Derived::Scalar & | x, |
| const ProductBase< Derived, Lhs, Rhs > & | prod | ||
| ) |
Definition at line 222 of file ProductBase.h.
| internal::enable_if<!internal::is_same<typename Derived::Scalar,typename Derived::RealScalar>::value, const ScaledProduct<Derived> >::type Eigen::operator* | ( | const typename Derived::RealScalar & | x, |
| const ProductBase< Derived, Lhs, Rhs > & | prod | ||
| ) |
Definition at line 228 of file ProductBase.h.
| const internal::transposition_matrix_product_retval<TranspositionsDerived, Derived, OnTheRight> Eigen::operator* | ( | const MatrixBase< Derived > & | matrix, |
| const TranspositionsBase< TranspositionsDerived > & | transpositions | ||
| ) | [inline] |
- Returns:
- the matrix with the transpositions applied to the columns.
Definition at line 331 of file Transpositions.h.
| const internal::transposition_matrix_product_retval<TranspositionDerived, Derived, OnTheLeft> Eigen::operator* | ( | const TranspositionsBase< TranspositionDerived > & | transpositions, |
| const MatrixBase< Derived > & | matrix | ||
| ) | [inline] |
- Returns:
- the matrix with the transpositions applied to the rows.
Definition at line 344 of file Transpositions.h.
| internal::matrix_type_times_scalar_type<typename VectorsType::Scalar,OtherDerived>::Type Eigen::operator* | ( | const MatrixBase< OtherDerived > & | other, |
| const HouseholderSequence< VectorsType, CoeffsType, Side > & | h | ||
| ) |
Computes the product of a matrix with a Householder sequence.
- Parameters:
-
[in] other Matrix being multiplied. [in] h HouseholderSequence being multiplied.
- Returns:
- Expression object representing the product.
This function computes 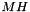 where
where  is the matrix
is the matrix other and  is the Householder sequence represented by
is the Householder sequence represented by h.
Definition at line 409 of file HouseholderSequence.h.
| const internal::permut_matrix_product_retval<PermutationDerived, Derived, OnTheRight> Eigen::operator* | ( | const MatrixBase< Derived > & | matrix, |
| const PermutationBase< PermutationDerived > & | permutation | ||
| ) | [inline] |
- Returns:
- the matrix with the permutation applied to the columns.
Definition at line 539 of file PermutationMatrix.h.
| const internal::permut_matrix_product_retval<PermutationDerived, Derived, OnTheLeft> Eigen::operator* | ( | const PermutationBase< PermutationDerived > & | permutation, |
| const MatrixBase< Derived > & | matrix | ||
| ) | [inline] |
- Returns:
- the matrix with the permutation applied to the rows.
Definition at line 552 of file PermutationMatrix.h.
| const Eigen::CwiseUnaryOp<Eigen::internal::scalar_inverse_mult_op<typename Derived::Scalar>, const Derived> Eigen::operator/ | ( | const typename Derived::Scalar & | s, |
| const Eigen::ArrayBase< Derived > & | a | ||
| ) | [inline] |
Component-wise division of a scalar by array elements.
Definition at line 74 of file GlobalFunctions.h.
| T Eigen::poly_eval | ( | const Polynomials & | poly, |
| const T & | x | ||
| ) | [inline] |
- Returns:
- the evaluation of the polynomial at x using stabilized Horner algorithm.
- Parameters:
-
[in] poly : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 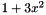 is stored as a vector
is stored as a vector ![$ [ 1, 0, 3 ] $](form_206.png) .
. [in] x : the value to evaluate the polynomial at.
Definition at line 46 of file PolynomialUtils.h.
| T Eigen::poly_eval_horner | ( | const Polynomials & | poly, |
| const T & | x | ||
| ) | [inline] |
- Returns:
- the evaluation of the polynomial at x using Horner algorithm.
- Parameters:
-
[in] poly : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 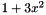 is stored as a vector
is stored as a vector ![$ [ 1, 0, 3 ] $](form_206.png) .
. [in] x : the value to evaluate the polynomial at.
Note for stability: 
Definition at line 28 of file PolynomialUtils.h.
| const Eigen::CwiseUnaryOp<Eigen::internal::scalar_pow_op<typename Derived::Scalar>, const Derived> Eigen::pow | ( | const Eigen::ArrayBase< Derived > & | x, |
| const typename Derived::Scalar & | exponent | ||
| ) | [inline] |
Definition at line 55 of file GlobalFunctions.h.
| const Eigen::CwiseBinaryOp<Eigen::internal::scalar_binary_pow_op<typename Derived::Scalar, typename Derived::Scalar>, const Derived, const Derived> Eigen::pow | ( | const Eigen::ArrayBase< Derived > & | x, |
| const Eigen::ArrayBase< Derived > & | exponents | ||
| ) | [inline] |
Definition at line 61 of file GlobalFunctions.h.
| const DerType Eigen::pow | ( | const Eigen::AutoDiffScalar< DerType > & | x, |
| typename Eigen::internal::traits< DerType >::Scalar | y | ||
| ) |
Definition at line 581 of file AutoDiffScalar.h.
| T Eigen::precision | ( | ) | [inline] |
Definition at line 30 of file Eigen/src/Eigen2Support/MathFunctions.h.
| const AutoDiffScalar<DerType>& Eigen::real | ( | const AutoDiffScalar< DerType > & | x | ) | [inline] |
Definition at line 535 of file AutoDiffScalar.h.
| return Eigen::ReturnType | ( | asin(x.value()) | , |
| x. | derivatives)*(Scalar(1)/sqrt(1-numext::abs2(x.value())) | ||
| ) |
| HouseholderSequence<VectorsType,CoeffsType,OnTheRight> Eigen::rightHouseholderSequence | ( | const VectorsType & | v, |
| const CoeffsType & | h | ||
| ) |
Convenience function for constructing a Householder sequence.
\
- Returns:
- A HouseholderSequence constructed from the specified arguments.
This function differs from householderSequence() in that the template argument OnTheSide of the constructed HouseholderSequence is set to OnTheRight, instead of the default OnTheLeft.
Definition at line 434 of file HouseholderSequence.h.
| void Eigen::roots_to_monicPolynomial | ( | const RootVector & | rv, |
| Polynomial & | poly | ||
| ) |
Given the roots of a polynomial compute the coefficients in the monomial basis of the monic polynomial with same roots and minimal degree. If RootVector is a vector of complexes, Polynomial should also be a vector of complexes.
- Parameters:
-
[in] rv : a vector containing the roots of a polynomial. [out] poly : the vector of coefficients of the polynomial ordered by degrees i.e. poly[i] is the coefficient of degree i of the polynomial e.g. 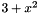 is stored as a vector
is stored as a vector ![$ [ 3, 0, 1 ] $](form_209.png) .
.
Definition at line 127 of file PolynomialUtils.h.
| bool Eigen::saveMarket | ( | const SparseMatrixType & | mat, |
| const std::string & | filename, | ||
| int | sym = 0 |
||
| ) |
Definition at line 224 of file MarketIO.h.
| bool Eigen::saveMarketVector | ( | const VectorType & | vec, |
| const std::string & | filename | ||
| ) |
Definition at line 250 of file MarketIO.h.
| static UniformScaling<float> Eigen::Scaling | ( | float | s | ) | [inline, static] |
Constructs a uniform scaling from scale factor s
Definition at line 115 of file Eigen/src/Geometry/Scaling.h.
| static UniformScaling<double> Eigen::Scaling | ( | double | s | ) | [inline, static] |
Constructs a uniform scaling from scale factor s
Definition at line 117 of file Eigen/src/Geometry/Scaling.h.
| static UniformScaling<std::complex<RealScalar> > Eigen::Scaling | ( | const std::complex< RealScalar > & | s | ) | [inline, static] |
Constructs a uniform scaling from scale factor s
Definition at line 120 of file Eigen/src/Geometry/Scaling.h.
| static DiagonalMatrix<Scalar,2> Eigen::Scaling | ( | const Scalar & | sx, |
| const Scalar & | sy | ||
| ) | [inline, static] |
Constructs a 2D axis aligned scaling
Definition at line 125 of file Eigen/src/Geometry/Scaling.h.
| static DiagonalMatrix<Scalar,3> Eigen::Scaling | ( | const Scalar & | sx, |
| const Scalar & | sy, | ||
| const Scalar & | sz | ||
| ) | [inline, static] |
Constructs a 3D axis aligned scaling
Definition at line 129 of file Eigen/src/Geometry/Scaling.h.
| static const DiagonalWrapper<const Derived> Eigen::Scaling | ( | const MatrixBase< Derived > & | coeffs | ) | [inline, static] |
Constructs an axis aligned scaling expression from vector expression coeffs This is an alias for coeffs.asDiagonal()
Definition at line 136 of file Eigen/src/Geometry/Scaling.h.
| void Eigen::setCpuCacheSizes | ( | std::ptrdiff_t | l1, |
| std::ptrdiff_t | l2 | ||
| ) | [inline] |
Set the cpu L1 and L2 cache sizes (in bytes). These values are use to adjust the size of the blocks for the algorithms working per blocks.
- See also:
- computeProductBlockingSizes
Definition at line 1334 of file GeneralBlockPanelKernel.h.
| void Eigen::setNbThreads | ( | int | v | ) | [inline] |
Sets the max number of threads reserved for Eigen
- See also:
- nbThreads
Definition at line 67 of file Parallelizer.h.
| void Eigen::ssaupd_ | ( | int * | ido, |
| char * | bmat, | ||
| int * | n, | ||
| char * | which, | ||
| int * | nev, | ||
| float * | tol, | ||
| float * | resid, | ||
| int * | ncv, | ||
| float * | v, | ||
| int * | ldv, | ||
| int * | iparam, | ||
| int * | ipntr, | ||
| float * | workd, | ||
| float * | workl, | ||
| int * | lworkl, | ||
| int * | info | ||
| ) |
| void Eigen::sseupd_ | ( | int * | rvec, |
| char * | All, | ||
| int * | select, | ||
| float * | d, | ||
| float * | z, | ||
| int * | ldz, | ||
| float * | sigma, | ||
| char * | bmat, | ||
| int * | n, | ||
| char * | which, | ||
| int * | nev, | ||
| float * | tol, | ||
| float * | resid, | ||
| int * | ncv, | ||
| float * | v, | ||
| int * | ldv, | ||
| int * | iparam, | ||
| int * | ipntr, | ||
| float * | workd, | ||
| float * | workl, | ||
| int * | lworkl, | ||
| int * | ierr | ||
| ) |
| void Eigen::umfpack_free_numeric | ( | void ** | Numeric, |
| double | |||
| ) | [inline] |
Definition at line 19 of file UmfPackSupport.h.
| void Eigen::umfpack_free_numeric | ( | void ** | Numeric, |
| std::complex< double > | |||
| ) | [inline] |
Definition at line 22 of file UmfPackSupport.h.
| void Eigen::umfpack_free_symbolic | ( | void ** | Symbolic, |
| double | |||
| ) | [inline] |
Definition at line 25 of file UmfPackSupport.h.
| void Eigen::umfpack_free_symbolic | ( | void ** | Symbolic, |
| std::complex< double > | |||
| ) | [inline] |
Definition at line 28 of file UmfPackSupport.h.
| int Eigen::umfpack_get_determinant | ( | double * | Mx, |
| double * | Ex, | ||
| void * | NumericHandle, | ||
| double | User_Info[UMFPACK_INFO] | ||
| ) | [inline] |
Definition at line 99 of file UmfPackSupport.h.
| int Eigen::umfpack_get_determinant | ( | std::complex< double > * | Mx, |
| double * | Ex, | ||
| void * | NumericHandle, | ||
| double | User_Info[UMFPACK_INFO] | ||
| ) | [inline] |
Definition at line 104 of file UmfPackSupport.h.
| int Eigen::umfpack_get_lunz | ( | int * | lnz, |
| int * | unz, | ||
| int * | n_row, | ||
| int * | n_col, | ||
| int * | nz_udiag, | ||
| void * | Numeric, | ||
| double | |||
| ) | [inline] |
Definition at line 73 of file UmfPackSupport.h.
| int Eigen::umfpack_get_lunz | ( | int * | lnz, |
| int * | unz, | ||
| int * | n_row, | ||
| int * | n_col, | ||
| int * | nz_udiag, | ||
| void * | Numeric, | ||
| std::complex< double > | |||
| ) | [inline] |
Definition at line 78 of file UmfPackSupport.h.
| int Eigen::umfpack_get_numeric | ( | int | Lp[], |
| int | Lj[], | ||
| double | Lx[], | ||
| int | Up[], | ||
| int | Ui[], | ||
| double | Ux[], | ||
| int | P[], | ||
| int | Q[], | ||
| double | Dx[], | ||
| int * | do_recip, | ||
| double | Rs[], | ||
| void * | Numeric | ||
| ) | [inline] |
Definition at line 83 of file UmfPackSupport.h.
| int Eigen::umfpack_get_numeric | ( | int | Lp[], |
| int | Lj[], | ||
| std::complex< double > | Lx[], | ||
| int | Up[], | ||
| int | Ui[], | ||
| std::complex< double > | Ux[], | ||
| int | P[], | ||
| int | Q[], | ||
| std::complex< double > | Dx[], | ||
| int * | do_recip, | ||
| double | Rs[], | ||
| void * | Numeric | ||
| ) | [inline] |
Definition at line 89 of file UmfPackSupport.h.
| int Eigen::umfpack_numeric | ( | const int | Ap[], |
| const int | Ai[], | ||
| const double | Ax[], | ||
| void * | Symbolic, | ||
| void ** | Numeric, | ||
| const double | Control[UMFPACK_CONTROL], | ||
| double | Info[UMFPACK_INFO] | ||
| ) | [inline] |
Definition at line 45 of file UmfPackSupport.h.
| int Eigen::umfpack_numeric | ( | const int | Ap[], |
| const int | Ai[], | ||
| const std::complex< double > | Ax[], | ||
| void * | Symbolic, | ||
| void ** | Numeric, | ||
| const double | Control[UMFPACK_CONTROL], | ||
| double | Info[UMFPACK_INFO] | ||
| ) | [inline] |
Definition at line 52 of file UmfPackSupport.h.
| int Eigen::umfpack_solve | ( | int | sys, |
| const int | Ap[], | ||
| const int | Ai[], | ||
| const double | Ax[], | ||
| double | X[], | ||
| const double | B[], | ||
| void * | Numeric, | ||
| const double | Control[UMFPACK_CONTROL], | ||
| double | Info[UMFPACK_INFO] | ||
| ) | [inline] |
Definition at line 59 of file UmfPackSupport.h.
| int Eigen::umfpack_solve | ( | int | sys, |
| const int | Ap[], | ||
| const int | Ai[], | ||
| const std::complex< double > | Ax[], | ||
| std::complex< double > | X[], | ||
| const std::complex< double > | B[], | ||
| void * | Numeric, | ||
| const double | Control[UMFPACK_CONTROL], | ||
| double | Info[UMFPACK_INFO] | ||
| ) | [inline] |
Definition at line 66 of file UmfPackSupport.h.
| int Eigen::umfpack_symbolic | ( | int | n_row, |
| int | n_col, | ||
| const int | Ap[], | ||
| const int | Ai[], | ||
| const double | Ax[], | ||
| void ** | Symbolic, | ||
| const double | Control[UMFPACK_CONTROL], | ||
| double | Info[UMFPACK_INFO] | ||
| ) | [inline] |
Definition at line 31 of file UmfPackSupport.h.
| int Eigen::umfpack_symbolic | ( | int | n_row, |
| int | n_col, | ||
| const int | Ap[], | ||
| const int | Ai[], | ||
| const std::complex< double > | Ax[], | ||
| void ** | Symbolic, | ||
| const double | Control[UMFPACK_CONTROL], | ||
| double | Info[UMFPACK_INFO] | ||
| ) | [inline] |
Definition at line 38 of file UmfPackSupport.h.
| cholmod_sparse Eigen::viewAsCholmod | ( | SparseMatrix< _Scalar, _Options, _Index > & | mat | ) |
Wraps the Eigen sparse matrix mat into a Cholmod sparse matrix object. Note that the data are shared.
Definition at line 52 of file CholmodSupport.h.
| const cholmod_sparse Eigen::viewAsCholmod | ( | const SparseMatrix< _Scalar, _Options, _Index > & | mat | ) |
Definition at line 99 of file CholmodSupport.h.
| cholmod_sparse Eigen::viewAsCholmod | ( | const SparseSelfAdjointView< SparseMatrix< _Scalar, _Options, _Index >, UpLo > & | mat | ) |
Returns a view of the Eigen sparse matrix mat as Cholmod sparse matrix. The data are not copied but shared.
Definition at line 108 of file CholmodSupport.h.
| cholmod_dense Eigen::viewAsCholmod | ( | MatrixBase< Derived > & | mat | ) |
Returns a view of the Eigen dense matrix mat as Cholmod dense matrix. The data are not copied but shared.
Definition at line 121 of file CholmodSupport.h.
| MappedSparseMatrix<Scalar,Flags,Index> Eigen::viewAsEigen | ( | cholmod_sparse & | cm | ) |
Returns a view of the Cholmod sparse matrix cm as an Eigen sparse matrix. The data are not copied but shared.
Definition at line 142 of file CholmodSupport.h.
Variable Documentation
| const unsigned int Eigen::ActualPacketAccessBit = 0x0 |
Definition at line 94 of file Constants.h.
| const int Eigen::CoherentAccessPattern = 0x1 |
Definition at line 65 of file SparseUtil.h.
| const int Eigen::Dynamic = -1 |
This value means that a positive quantity (e.g., a size) is not known at compile-time, and that instead the value is stored in some runtime variable.
Changing the value of Dynamic breaks the ABI, as Dynamic is often used as a template parameter for Matrix.
Definition at line 21 of file Constants.h.
| const int Eigen::DynamicIndex = 0xffffff |
This value means that a signed quantity (e.g., a signed index) is not known at compile-time, and that instead its value has to be specified at runtime.
Definition at line 26 of file Constants.h.
| const unsigned int Eigen::HereditaryBits |
Definition at line 152 of file Constants.h.
| const int Eigen::Infinity = -1 |
This value means +Infinity; it is currently used only as the p parameter to MatrixBase::lpNorm<int>(). The value Infinity there means the L-infinity norm.
Definition at line 31 of file Constants.h.
| const int Eigen::InnerRandomAccessPattern = 0x2 | CoherentAccessPattern |
Definition at line 66 of file SparseUtil.h.
| const unsigned int Eigen::LowerTriangular = Lower |
Definition at line 21 of file Eigen2Support/TriangularSolver.h.
| const unsigned int Eigen::LowerTriangularBit = Lower |
Definition at line 18 of file Eigen2Support/TriangularSolver.h.
| const unsigned int Eigen::NestByRefBit = 0x100 |
Definition at line 149 of file Constants.h.
| const int Eigen::OuterRandomAccessPattern = 0x4 | CoherentAccessPattern |
Definition at line 67 of file SparseUtil.h.
| const int Eigen::RandomAccessPattern = 0x8 | OuterRandomAccessPattern | InnerRandomAccessPattern |
Definition at line 68 of file SparseUtil.h.
| const unsigned int Eigen::SelfAdjointBit = SelfAdjoint |
Definition at line 16 of file Eigen2Support/TriangularSolver.h.
| const unsigned int Eigen::SkylineBit = 0x1200 |
Definition at line 21 of file SkylineUtil.h.
| const unsigned int Eigen::UnitDiagBit = UnitDiag |
Definition at line 15 of file Eigen2Support/TriangularSolver.h.
| const unsigned int Eigen::UnitLowerTriangular = UnitLower |
Definition at line 23 of file Eigen2Support/TriangularSolver.h.
| const unsigned int Eigen::UnitUpperTriangular = UnitUpper |
Definition at line 22 of file Eigen2Support/TriangularSolver.h.
| const unsigned int Eigen::UpperTriangular = Upper |
Definition at line 20 of file Eigen2Support/TriangularSolver.h.
| const unsigned int Eigen::UpperTriangularBit = Upper |
Definition at line 17 of file Eigen2Support/TriangularSolver.h.