Robust Cholesky decomposition of a matrix with pivoting. More...
#include <LDLT.h>
Public Types | |
| enum | { RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options & ~RowMajorBit, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime, UpLo = _UpLo } |
| typedef MatrixType::Index | Index |
| typedef _MatrixType | MatrixType |
| typedef PermutationMatrix < RowsAtCompileTime, MaxRowsAtCompileTime > | PermutationType |
| typedef NumTraits< typename MatrixType::Scalar >::Real | RealScalar |
| typedef MatrixType::Scalar | Scalar |
| typedef Matrix< Scalar, RowsAtCompileTime, 1, Options, MaxRowsAtCompileTime, 1 > | TmpMatrixType |
| typedef internal::LDLT_Traits < MatrixType, UpLo > | Traits |
| typedef Transpositions < RowsAtCompileTime, MaxRowsAtCompileTime > | TranspositionType |
Public Member Functions | |
| Index | cols () const |
| LDLT & | compute (const MatrixType &matrix) |
| ComputationInfo | info () const |
| Reports whether previous computation was successful. | |
| bool | isNegative (void) const |
| bool | isPositive () const |
| LDLT () | |
| Default Constructor. | |
| LDLT (Index size) | |
| Default Constructor with memory preallocation. | |
| LDLT (const MatrixType &matrix) | |
| Constructor with decomposition. | |
| Traits::MatrixL | matrixL () const |
| const MatrixType & | matrixLDLT () const |
| Traits::MatrixU | matrixU () const |
| template<typename Derived > | |
| LDLT & | rankUpdate (const MatrixBase< Derived > &w, const RealScalar &alpha=1) |
| template<typename Derived > | |
| LDLT< MatrixType, _UpLo > & | rankUpdate (const MatrixBase< Derived > &w, const typename NumTraits< typename MatrixType::Scalar >::Real &sigma) |
| MatrixType | reconstructedMatrix () const |
| Index | rows () const |
| void | setZero () |
| template<typename Rhs > | |
| const internal::solve_retval < LDLT, Rhs > | solve (const MatrixBase< Rhs > &b) const |
| template<typename Derived > | |
| bool | solveInPlace (MatrixBase< Derived > &bAndX) const |
| const TranspositionType & | transpositionsP () const |
| Diagonal< const MatrixType > | vectorD () const |
Static Protected Member Functions | |
| static void | check_template_parameters () |
Protected Attributes | |
| bool | m_isInitialized |
| MatrixType | m_matrix |
| internal::SignMatrix | m_sign |
| TmpMatrixType | m_temporary |
| TranspositionType | m_transpositions |
Detailed Description
template<typename _MatrixType, int _UpLo>
class Eigen::LDLT< _MatrixType, _UpLo >
Robust Cholesky decomposition of a matrix with pivoting.
- Parameters:
-
MatrixType the type of the matrix of which to compute the LDL^T Cholesky decomposition UpLo the triangular part that will be used for the decompositon: Lower (default) or Upper. The other triangular part won't be read.
Perform a robust Cholesky decomposition of a positive semidefinite or negative semidefinite matrix 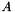 such that
such that 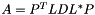 , where P is a permutation matrix, L is lower triangular with a unit diagonal and D is a diagonal matrix.
, where P is a permutation matrix, L is lower triangular with a unit diagonal and D is a diagonal matrix.
The decomposition uses pivoting to ensure stability, so that L will have zeros in the bottom right rank(A) - n submatrix. Avoiding the square root on D also stabilizes the computation.
Remember that Cholesky decompositions are not rank-revealing. Also, do not use a Cholesky decomposition to determine whether a system of equations has a solution.
- See also:
- MatrixBase::ldlt(), class LLT
Member Typedef Documentation
| typedef MatrixType::Index Eigen::LDLT< _MatrixType, _UpLo >::Index |
| typedef _MatrixType Eigen::LDLT< _MatrixType, _UpLo >::MatrixType |
| typedef PermutationMatrix<RowsAtCompileTime, MaxRowsAtCompileTime> Eigen::LDLT< _MatrixType, _UpLo >::PermutationType |
| typedef NumTraits<typename MatrixType::Scalar>::Real Eigen::LDLT< _MatrixType, _UpLo >::RealScalar |
| typedef MatrixType::Scalar Eigen::LDLT< _MatrixType, _UpLo >::Scalar |
| typedef Matrix<Scalar, RowsAtCompileTime, 1, Options, MaxRowsAtCompileTime, 1> Eigen::LDLT< _MatrixType, _UpLo >::TmpMatrixType |
| typedef internal::LDLT_Traits<MatrixType,UpLo> Eigen::LDLT< _MatrixType, _UpLo >::Traits |
| typedef Transpositions<RowsAtCompileTime, MaxRowsAtCompileTime> Eigen::LDLT< _MatrixType, _UpLo >::TranspositionType |
Member Enumeration Documentation
| anonymous enum |
Constructor & Destructor Documentation
| Eigen::LDLT< _MatrixType, _UpLo >::LDLT | ( | ) | [inline] |
Default Constructor.
The default constructor is useful in cases in which the user intends to perform decompositions via LDLT::compute(const MatrixType&).
| Eigen::LDLT< _MatrixType, _UpLo >::LDLT | ( | Index | size | ) | [inline] |
| Eigen::LDLT< _MatrixType, _UpLo >::LDLT | ( | const MatrixType & | matrix | ) | [inline] |
Constructor with decomposition.
This calculates the decomposition for the input matrix.
- See also:
- LDLT(Index size)
Member Function Documentation
| static void Eigen::LDLT< _MatrixType, _UpLo >::check_template_parameters | ( | ) | [inline, static, protected] |
| Index Eigen::LDLT< _MatrixType, _UpLo >::cols | ( | ) | const [inline] |
| LDLT< MatrixType, _UpLo > & Eigen::LDLT< MatrixType, _UpLo >::compute | ( | const MatrixType & | a | ) |
| ComputationInfo Eigen::LDLT< _MatrixType, _UpLo >::info | ( | ) | const [inline] |
| bool Eigen::LDLT< _MatrixType, _UpLo >::isNegative | ( | void | ) | const [inline] |
| bool Eigen::LDLT< _MatrixType, _UpLo >::isPositive | ( | ) | const [inline] |
| Traits::MatrixL Eigen::LDLT< _MatrixType, _UpLo >::matrixL | ( | ) | const [inline] |
| const MatrixType& Eigen::LDLT< _MatrixType, _UpLo >::matrixLDLT | ( | ) | const [inline] |
| Traits::MatrixU Eigen::LDLT< _MatrixType, _UpLo >::matrixU | ( | ) | const [inline] |
| LDLT& Eigen::LDLT< _MatrixType, _UpLo >::rankUpdate | ( | const MatrixBase< Derived > & | w, |
| const RealScalar & | alpha = 1 |
||
| ) |
| LDLT<MatrixType,_UpLo>& Eigen::LDLT< _MatrixType, _UpLo >::rankUpdate | ( | const MatrixBase< Derived > & | w, |
| const typename NumTraits< typename MatrixType::Scalar >::Real & | sigma | ||
| ) |
Update the LDLT decomposition: given A = L D L^T, efficiently compute the decomposition of A + sigma w w^T.
- Parameters:
-
w a vector to be incorporated into the decomposition. sigma a scalar, +1 for updates and -1 for "downdates," which correspond to removing previously-added column vectors. Optional; default value is +1.
- See also:
- setZero()
| MatrixType Eigen::LDLT< MatrixType, _UpLo >::reconstructedMatrix | ( | ) | const |
| Index Eigen::LDLT< _MatrixType, _UpLo >::rows | ( | ) | const [inline] |
| void Eigen::LDLT< _MatrixType, _UpLo >::setZero | ( | ) | [inline] |
| const internal::solve_retval<LDLT, Rhs> Eigen::LDLT< _MatrixType, _UpLo >::solve | ( | const MatrixBase< Rhs > & | b | ) | const [inline] |
- Returns:
- a solution x of
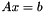 using the current decomposition of A.
using the current decomposition of A.
This function also supports in-place solves using the syntax x = decompositionObject.solve(x) .
More precisely, this method solves 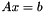 using the decomposition
using the decomposition 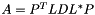 by solving the systems
by solving the systems 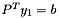 ,
, 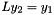 ,
, 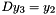 ,
, 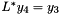 and
and 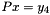 in succession. If the matrix
in succession. If the matrix 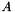 is singular, then
is singular, then 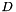 will also be singular (all the other matrices are invertible). In that case, the least-square solution of
will also be singular (all the other matrices are invertible). In that case, the least-square solution of 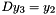 is computed. This does not mean that this function computes the least-square solution of
is computed. This does not mean that this function computes the least-square solution of 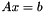 is
is 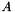 is singular.
is singular.
- See also:
- MatrixBase::ldlt()
| bool Eigen::LDLT< MatrixType, _UpLo >::solveInPlace | ( | MatrixBase< Derived > & | bAndX | ) | const |
| const TranspositionType& Eigen::LDLT< _MatrixType, _UpLo >::transpositionsP | ( | ) | const [inline] |
| Diagonal<const MatrixType> Eigen::LDLT< _MatrixType, _UpLo >::vectorD | ( | ) | const [inline] |
Member Data Documentation
bool Eigen::LDLT< _MatrixType, _UpLo >::m_isInitialized [protected] |
MatrixType Eigen::LDLT< _MatrixType, _UpLo >::m_matrix [protected] |
internal::SignMatrix Eigen::LDLT< _MatrixType, _UpLo >::m_sign [protected] |
TmpMatrixType Eigen::LDLT< _MatrixType, _UpLo >::m_temporary [protected] |
TranspositionType Eigen::LDLT< _MatrixType, _UpLo >::m_transpositions [protected] |
The documentation for this class was generated from the following file: