Computes the generalized eigenvalues and eigenvectors of a pair of general matrices. More...
#include <GeneralizedEigenSolver.h>
Public Types | |
| enum | { RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime } |
| typedef std::complex< RealScalar > | ComplexScalar |
| Complex scalar type for MatrixType. | |
| typedef Matrix< ComplexScalar, ColsAtCompileTime, 1, Options &~RowMajor, MaxColsAtCompileTime, 1 > | ComplexVectorType |
| Type for vector of complex scalar values eigenvalues as returned by betas(). | |
| typedef CwiseBinaryOp < internal::scalar_quotient_op < ComplexScalar, Scalar > , ComplexVectorType, VectorType > | EigenvalueType |
| Expression type for the eigenvalues as returned by eigenvalues(). | |
| typedef Matrix< ComplexScalar, RowsAtCompileTime, ColsAtCompileTime, Options, MaxRowsAtCompileTime, MaxColsAtCompileTime > | EigenvectorsType |
| Type for matrix of eigenvectors as returned by eigenvectors(). | |
| typedef MatrixType::Index | Index |
| typedef _MatrixType | MatrixType |
Synonym for the template parameter _MatrixType. | |
| typedef NumTraits< Scalar >::Real | RealScalar |
| typedef MatrixType::Scalar | Scalar |
| Scalar type for matrices of type MatrixType. | |
| typedef Matrix< Scalar, ColsAtCompileTime, 1, Options &~RowMajor, MaxColsAtCompileTime, 1 > | VectorType |
| Type for vector of real scalar values eigenvalues as returned by betas(). | |
Public Member Functions | |
| ComplexVectorType | alphas () const |
| VectorType | betas () const |
| GeneralizedEigenSolver & | compute (const MatrixType &A, const MatrixType &B, bool computeEigenvectors=true) |
| Computes generalized eigendecomposition of given matrix. | |
| EigenvalueType | eigenvalues () const |
| Returns an expression of the computed generalized eigenvalues. | |
| GeneralizedEigenSolver () | |
| Default constructor. | |
| GeneralizedEigenSolver (Index size) | |
| Default constructor with memory preallocation. | |
| GeneralizedEigenSolver (const MatrixType &A, const MatrixType &B, bool computeEigenvectors=true) | |
| Constructor; computes the generalized eigendecomposition of given matrix pair. | |
| ComputationInfo | info () const |
| GeneralizedEigenSolver & | setMaxIterations (Index maxIters) |
Protected Types | |
| typedef Matrix< Scalar, ColsAtCompileTime, 1, Options &~RowMajor, MaxColsAtCompileTime, 1 > | ColumnVectorType |
Static Protected Member Functions | |
| static void | check_template_parameters () |
Protected Attributes | |
| ComplexVectorType | m_alphas |
| VectorType | m_betas |
| bool | m_eigenvectorsOk |
| MatrixType | m_eivec |
| bool | m_isInitialized |
| MatrixType | m_matS |
| RealQZ< MatrixType > | m_realQZ |
| ColumnVectorType | m_tmp |
Detailed Description
template<typename _MatrixType>
class Eigen::GeneralizedEigenSolver< _MatrixType >
Computes the generalized eigenvalues and eigenvectors of a pair of general matrices.
- Template Parameters:
-
_MatrixType the type of the matrices of which we are computing the eigen-decomposition; this is expected to be an instantiation of the Matrix class template. Currently, only real matrices are supported.
The generalized eigenvalues and eigenvectors of a matrix pair 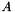 and
and 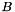 are scalars
are scalars 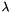 and vectors
and vectors 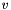 such that
such that 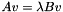 . If
. If 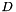 is a diagonal matrix with the eigenvalues on the diagonal, and
is a diagonal matrix with the eigenvalues on the diagonal, and 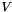 is a matrix with the eigenvectors as its columns, then
is a matrix with the eigenvectors as its columns, then 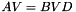 . The matrix
. The matrix 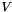 is almost always invertible, in which case we have
is almost always invertible, in which case we have 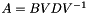 . This is called the generalized eigen-decomposition.
. This is called the generalized eigen-decomposition.
The generalized eigenvalues and eigenvectors of a matrix pair may be complex, even when the matrices are real. Moreover, the generalized eigenvalue might be infinite if the matrix B is singular. To workaround this difficulty, the eigenvalues are provided as a pair of complex 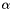 and real
and real 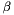 such that:
such that: 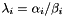 . If
. If 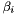 is (nearly) zero, then one can consider the well defined left eigenvalue
is (nearly) zero, then one can consider the well defined left eigenvalue 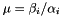 such that:
such that: 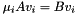 , or even
, or even 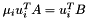 where
where 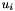 is called the left eigenvector.
is called the left eigenvector.
Call the function compute() to compute the generalized eigenvalues and eigenvectors of a given matrix pair. Alternatively, you can use the GeneralizedEigenSolver(const MatrixType&, const MatrixType&, bool) constructor which computes the eigenvalues and eigenvectors at construction time. Once the eigenvalue and eigenvectors are computed, they can be retrieved with the eigenvalues() and eigenvectors() functions.
Here is an usage example of this class: Example:
Output:
- See also:
- MatrixBase::eigenvalues(), class ComplexEigenSolver, class SelfAdjointEigenSolver
Definition at line 57 of file GeneralizedEigenSolver.h.
Member Typedef Documentation
typedef Matrix<Scalar, ColsAtCompileTime, 1, Options & ~RowMajor, MaxColsAtCompileTime, 1> Eigen::GeneralizedEigenSolver< _MatrixType >::ColumnVectorType [protected] |
Definition at line 281 of file GeneralizedEigenSolver.h.
| typedef std::complex<RealScalar> Eigen::GeneralizedEigenSolver< _MatrixType >::ComplexScalar |
Complex scalar type for MatrixType.
This is std::complex<Scalar> if Scalar is real (e.g., float or double) and just Scalar if Scalar is complex.
Definition at line 83 of file GeneralizedEigenSolver.h.
| typedef Matrix<ComplexScalar, ColsAtCompileTime, 1, Options & ~RowMajor, MaxColsAtCompileTime, 1> Eigen::GeneralizedEigenSolver< _MatrixType >::ComplexVectorType |
Type for vector of complex scalar values eigenvalues as returned by betas().
This is a column vector with entries of type ComplexScalar. The length of the vector is the size of MatrixType.
Definition at line 97 of file GeneralizedEigenSolver.h.
| typedef CwiseBinaryOp<internal::scalar_quotient_op<ComplexScalar,Scalar>,ComplexVectorType,VectorType> Eigen::GeneralizedEigenSolver< _MatrixType >::EigenvalueType |
Expression type for the eigenvalues as returned by eigenvalues().
Definition at line 101 of file GeneralizedEigenSolver.h.
| typedef Matrix<ComplexScalar, RowsAtCompileTime, ColsAtCompileTime, Options, MaxRowsAtCompileTime, MaxColsAtCompileTime> Eigen::GeneralizedEigenSolver< _MatrixType >::EigenvectorsType |
Type for matrix of eigenvectors as returned by eigenvectors().
This is a square matrix with entries of type ComplexScalar. The size is the same as the size of MatrixType.
Definition at line 108 of file GeneralizedEigenSolver.h.
| typedef MatrixType::Index Eigen::GeneralizedEigenSolver< _MatrixType >::Index |
Definition at line 75 of file GeneralizedEigenSolver.h.
| typedef _MatrixType Eigen::GeneralizedEigenSolver< _MatrixType >::MatrixType |
Synonym for the template parameter _MatrixType.
Definition at line 62 of file GeneralizedEigenSolver.h.
| typedef NumTraits<Scalar>::Real Eigen::GeneralizedEigenSolver< _MatrixType >::RealScalar |
Definition at line 74 of file GeneralizedEigenSolver.h.
| typedef MatrixType::Scalar Eigen::GeneralizedEigenSolver< _MatrixType >::Scalar |
Scalar type for matrices of type MatrixType.
Definition at line 73 of file GeneralizedEigenSolver.h.
| typedef Matrix<Scalar, ColsAtCompileTime, 1, Options & ~RowMajor, MaxColsAtCompileTime, 1> Eigen::GeneralizedEigenSolver< _MatrixType >::VectorType |
Type for vector of real scalar values eigenvalues as returned by betas().
This is a column vector with entries of type Scalar. The length of the vector is the size of MatrixType.
Definition at line 90 of file GeneralizedEigenSolver.h.
Member Enumeration Documentation
| anonymous enum |
Definition at line 64 of file GeneralizedEigenSolver.h.
Constructor & Destructor Documentation
| Eigen::GeneralizedEigenSolver< _MatrixType >::GeneralizedEigenSolver | ( | ) | [inline] |
Default constructor.
The default constructor is useful in cases in which the user intends to perform decompositions via EigenSolver::compute(const MatrixType&, bool).
- See also:
- compute() for an example.
Definition at line 117 of file GeneralizedEigenSolver.h.
| Eigen::GeneralizedEigenSolver< _MatrixType >::GeneralizedEigenSolver | ( | Index | size | ) | [inline] |
Default constructor with memory preallocation.
Like the default constructor but with preallocation of the internal data according to the specified problem size.
- See also:
- GeneralizedEigenSolver()
Definition at line 125 of file GeneralizedEigenSolver.h.
| Eigen::GeneralizedEigenSolver< _MatrixType >::GeneralizedEigenSolver | ( | const MatrixType & | A, |
| const MatrixType & | B, | ||
| bool | computeEigenvectors = true |
||
| ) | [inline] |
Constructor; computes the generalized eigendecomposition of given matrix pair.
- Parameters:
-
[in] A Square matrix whose eigendecomposition is to be computed. [in] B Square matrix whose eigendecomposition is to be computed. [in] computeEigenvectors If true, both the eigenvectors and the eigenvalues are computed; if false, only the eigenvalues are computed.
This constructor calls compute() to compute the generalized eigenvalues and eigenvectors.
- See also:
- compute()
Definition at line 148 of file GeneralizedEigenSolver.h.
Member Function Documentation
| ComplexVectorType Eigen::GeneralizedEigenSolver< _MatrixType >::alphas | ( | ) | const [inline] |
- Returns:
- A const reference to the vectors containing the alpha values
This vector permits to reconstruct the j-th eigenvalues as alphas(i)/betas(j).
- See also:
- betas(), eigenvalues()
Definition at line 209 of file GeneralizedEigenSolver.h.
| VectorType Eigen::GeneralizedEigenSolver< _MatrixType >::betas | ( | ) | const [inline] |
- Returns:
- A const reference to the vectors containing the beta values
This vector permits to reconstruct the j-th eigenvalues as alphas(i)/betas(j).
- See also:
- alphas(), eigenvalues()
Definition at line 220 of file GeneralizedEigenSolver.h.
| static void Eigen::GeneralizedEigenSolver< _MatrixType >::check_template_parameters | ( | ) | [inline, static, protected] |
Definition at line 267 of file GeneralizedEigenSolver.h.
| GeneralizedEigenSolver< MatrixType > & Eigen::GeneralizedEigenSolver< MatrixType >::compute | ( | const MatrixType & | A, |
| const MatrixType & | B, | ||
| bool | computeEigenvectors = true |
||
| ) |
Computes generalized eigendecomposition of given matrix.
- Parameters:
-
[in] A Square matrix whose eigendecomposition is to be computed. [in] B Square matrix whose eigendecomposition is to be computed. [in] computeEigenvectors If true, both the eigenvectors and the eigenvalues are computed; if false, only the eigenvalues are computed.
- Returns:
- Reference to
*this
This function computes the eigenvalues of the real matrix matrix. The eigenvalues() function can be used to retrieve them. If computeEigenvectors is true, then the eigenvectors are also computed and can be retrieved by calling eigenvectors().
The matrix is first reduced to real generalized Schur form using the RealQZ class. The generalized Schur decomposition is then used to compute the eigenvalues and eigenvectors.
The cost of the computation is dominated by the cost of the generalized Schur decomposition.
This method reuses of the allocated data in the GeneralizedEigenSolver object.
Definition at line 298 of file GeneralizedEigenSolver.h.
| EigenvalueType Eigen::GeneralizedEigenSolver< _MatrixType >::eigenvalues | ( | ) | const [inline] |
Returns an expression of the computed generalized eigenvalues.
- Returns:
- An expression of the column vector containing the eigenvalues.
It is a shortcut for
Not that betas might contain zeros. It is therefore not recommended to use this function, but rather directly deal with the alphas and betas vectors.
- Precondition:
- Either the constructor GeneralizedEigenSolver(const MatrixType&,const MatrixType&,bool) or the member function compute(const MatrixType&,const MatrixType&,bool) has been called before.
The eigenvalues are repeated according to their algebraic multiplicity, so there are as many eigenvalues as rows in the matrix. The eigenvalues are not sorted in any particular order.
Definition at line 198 of file GeneralizedEigenSolver.h.
| ComputationInfo Eigen::GeneralizedEigenSolver< _MatrixType >::info | ( | ) | const [inline] |
Definition at line 251 of file GeneralizedEigenSolver.h.
| GeneralizedEigenSolver& Eigen::GeneralizedEigenSolver< _MatrixType >::setMaxIterations | ( | Index | maxIters | ) | [inline] |
Sets the maximal number of iterations allowed.
Definition at line 259 of file GeneralizedEigenSolver.h.
Member Data Documentation
ComplexVectorType Eigen::GeneralizedEigenSolver< _MatrixType >::m_alphas [protected] |
Definition at line 274 of file GeneralizedEigenSolver.h.
VectorType Eigen::GeneralizedEigenSolver< _MatrixType >::m_betas [protected] |
Definition at line 275 of file GeneralizedEigenSolver.h.
bool Eigen::GeneralizedEigenSolver< _MatrixType >::m_eigenvectorsOk [protected] |
Definition at line 277 of file GeneralizedEigenSolver.h.
MatrixType Eigen::GeneralizedEigenSolver< _MatrixType >::m_eivec [protected] |
Definition at line 273 of file GeneralizedEigenSolver.h.
bool Eigen::GeneralizedEigenSolver< _MatrixType >::m_isInitialized [protected] |
Definition at line 276 of file GeneralizedEigenSolver.h.
MatrixType Eigen::GeneralizedEigenSolver< _MatrixType >::m_matS [protected] |
Definition at line 279 of file GeneralizedEigenSolver.h.
RealQZ<MatrixType> Eigen::GeneralizedEigenSolver< _MatrixType >::m_realQZ [protected] |
Definition at line 278 of file GeneralizedEigenSolver.h.
ColumnVectorType Eigen::GeneralizedEigenSolver< _MatrixType >::m_tmp [protected] |
Definition at line 282 of file GeneralizedEigenSolver.h.
The documentation for this class was generated from the following file: