Standard Cholesky decomposition (LL^T) of a matrix and associated features. More...

#include <LLT.h>

Inheritance diagram for Eigen::LLT< _MatrixType, _UpLo >:

Public Types
enum	{ MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }

enum	{ PacketSize = internal::packet_traits<Scalar>::size, AlignmentMask = int(PacketSize)-1, UpLo = _UpLo }

typedef SolverBase< LLT >	Base

typedef _MatrixType	MatrixType

typedef internal::LLT_Traits< MatrixType, UpLo >	Traits

Public Types inherited from Eigen::SolverBase< LLT< _MatrixType, _UpLo > >
enum

typedef internal::conditional< NumTraits< Scalar >::IsComplex, CwiseUnaryOp< internal::scalar_conjugate_op< Scalar >, ConstTransposeReturnType >, ConstTransposeReturnType >::type	AdjointReturnType

typedef EigenBase< LLT< _MatrixType, _UpLo > >	Base

typedef Scalar	CoeffReturnType

typedef internal::add_const< Transpose< const LLT< _MatrixType, _UpLo > > >::type	ConstTransposeReturnType

typedef internal::traits< LLT< _MatrixType, _UpLo > >::Scalar	Scalar

Public Types inherited from Eigen::EigenBase< Derived >
typedef Eigen::Index	Index
	The interface type of indices. More...

typedef internal::traits< Derived >::StorageKind	StorageKind

Public Member Functions
template<typename RhsType , typename DstType >
void	_solve_impl (const RhsType &rhs, DstType &dst) const

template<bool Conjugate, typename RhsType , typename DstType >
void	_solve_impl_transposed (const RhsType &rhs, DstType &dst) const

const LLT &	adjoint () const EIGEN_NOEXCEPT

EIGEN_CONSTEXPR Index	cols () const EIGEN_NOEXCEPT

template<typename InputType >
LLT &	compute (const EigenBase< InputType > &matrix)

template<typename InputType >
LLT< MatrixType, _UpLo > &	compute (const EigenBase< InputType > &a)

ComputationInfo	info () const
	Reports whether previous computation was successful. More...

	LLT ()
	Default Constructor. More...

	LLT (Index size)
	Default Constructor with memory preallocation. More...

template<typename InputType >
	LLT (const EigenBase< InputType > &matrix)

template<typename InputType >
	LLT (EigenBase< InputType > &matrix)
	Constructs a LLT factorization from a given matrix. More...

Traits::MatrixL	matrixL () const

const MatrixType &	matrixLLT () const

Traits::MatrixU	matrixU () const

template<typename VectorType >
LLT &	rankUpdate (const VectorType &vec, const RealScalar &sigma=1)

template<typename VectorType >
LLT< _MatrixType, _UpLo > &	rankUpdate (const VectorType &v, const RealScalar &sigma)

RealScalar	rcond () const

MatrixType	reconstructedMatrix () const

EIGEN_CONSTEXPR Index	rows () const EIGEN_NOEXCEPT

template<typename Derived >
void	solveInPlace (const MatrixBase< Derived > &bAndX) const

Public Member Functions inherited from Eigen::SolverBase< LLT< _MatrixType, _UpLo > >
AdjointReturnType	adjoint () const

const Solve< LLT< _MatrixType, _UpLo >, Rhs >	solve (const MatrixBase< Rhs > &b) const

	SolverBase ()

ConstTransposeReturnType	transpose () const

	~SolverBase ()

Public Member Functions inherited from Eigen::EigenBase< Derived >
template<typename Dest >
EIGEN_DEVICE_FUNC void	addTo (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	applyThisOnTheLeft (Dest &dst) const

template<typename Dest >
EIGEN_DEVICE_FUNC void	applyThisOnTheRight (Dest &dst) const

EIGEN_DEVICE_FUNC EIGEN_CONSTEXPR Index	cols () const EIGEN_NOEXCEPT

EIGEN_DEVICE_FUNC Derived &	const_cast_derived () const

EIGEN_DEVICE_FUNC const Derived &	const_derived () const

EIGEN_DEVICE_FUNC Derived &	derived ()

EIGEN_DEVICE_FUNC const Derived &	derived () const

template<typename Dest >
EIGEN_DEVICE_FUNC void	evalTo (Dest &dst) const

EIGEN_DEVICE_FUNC EIGEN_CONSTEXPR Index	rows () const EIGEN_NOEXCEPT

EIGEN_DEVICE_FUNC EIGEN_CONSTEXPR Index	size () const EIGEN_NOEXCEPT

template<typename Dest >
EIGEN_DEVICE_FUNC void	subTo (Dest &dst) const

Static Protected Member Functions
static void	check_template_parameters ()

Protected Attributes
ComputationInfo	m_info

bool	m_isInitialized

RealScalar	m_l1_norm

MatrixType	m_matrix

Friends
class	SolverBase< LLT >

Additional Inherited Members
Protected Member Functions inherited from Eigen::SolverBase< LLT< _MatrixType, _UpLo > >
void	_check_solve_assertion (const Rhs &b) const

Detailed Description

template<typename _MatrixType, int _UpLo>
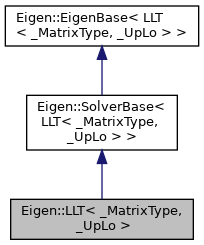
class Eigen::LLT< _MatrixType, _UpLo >

Standard Cholesky decomposition (LL^T) of a matrix and associated features.

Template Parameters

_MatrixType	the type of the matrix of which we are computing the LL^T Cholesky decomposition
_UpLo	the triangular part that will be used for the decompositon: Lower (default) or Upper. The other triangular part won't be read.

This class performs a LL^T Cholesky decomposition of a symmetric, positive definite matrix A such that A = LL^* = U^*U, where L is lower triangular.

While the Cholesky decomposition is particularly useful to solve selfadjoint problems like D^*D x = b, for that purpose, we recommend the Cholesky decomposition without square root which is more stable and even faster. Nevertheless, this standard Cholesky decomposition remains useful in many other situations like generalised eigen problems with hermitian matrices.

Remember that Cholesky decompositions are not rank-revealing. This LLT decomposition is only stable on positive definite matrices, use LDLT instead for the semidefinite case. Also, do not use a Cholesky decomposition to determine whether a system of equations has a solution.

Example:

MatrixXd A(3,3);
A << 4,-1,2, -1,6,0, 2,0,5;
cout << "The matrix A is" << endl << A << endl;
LLT<MatrixXd> lltOfA(A); // compute the Cholesky decomposition of A
MatrixXd L = lltOfA.matrixL(); // retrieve factor L  in the decomposition
// The previous two lines can also be written as "L = A.llt().matrixL()"
cout << "The Cholesky factor L is" << endl << L << endl;
cout << "To check this, let us compute L * L.transpose()" << endl;
cout << L * L.transpose() << endl;
cout << "This should equal the matrix A" << endl;

Output:

Performance: for best performance, it is recommended to use a column-major storage format with the Lower triangular part (the default), or, equivalently, a row-major storage format with the Upper triangular part. Otherwise, you might get a 20% slowdown for the full factorization step, and rank-updates can be up to 3 times slower.

This class supports the inplace decomposition mechanism.

Note that during the decomposition, only the lower (or upper, as defined by _UpLo) triangular part of A is considered. Therefore, the strict lower part does not have to store correct values.

See also: MatrixBase::llt(), SelfAdjointView::llt(), class LDLT

Definition at line 66 of file LLT.h.

Member Typedef Documentation

◆ Base

template<typename _MatrixType, int _UpLo>

typedef SolverBase<LLT> Eigen::LLT< _MatrixType, _UpLo >::Base

Definition at line 71 of file LLT.h.

◆ MatrixType

template<typename _MatrixType, int _UpLo>

typedef _MatrixType Eigen::LLT< _MatrixType, _UpLo >::MatrixType

Definition at line 70 of file LLT.h.

◆ Traits

template<typename _MatrixType, int _UpLo>

typedef internal::LLT_Traits<MatrixType,UpLo> Eigen::LLT< _MatrixType, _UpLo >::Traits

Definition at line 85 of file LLT.h.

Member Enumeration Documentation

◆ anonymous enum

template<typename _MatrixType, int _UpLo>

anonymous enum

Enumerator
MaxColsAtCompileTime

Definition at line 75 of file LLT.h.

◆ anonymous enum

template<typename _MatrixType, int _UpLo>

anonymous enum

Enumerator
PacketSize
AlignmentMask
UpLo

Definition at line 79 of file LLT.h.

Constructor & Destructor Documentation

◆ LLT() [1/4]

template<typename _MatrixType, int _UpLo>

Eigen::LLT< _MatrixType, _UpLo >::LLT ( )

inline

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via LLT::compute(const MatrixType&).

Definition at line 93 of file LLT.h.

◆ LLT() [2/4]

template<typename _MatrixType, int _UpLo>

Eigen::LLT< _MatrixType, _UpLo >::LLT ( Index size )

inlineexplicit

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See also: LLT()

Definition at line 101 of file LLT.h.

◆ LLT() [3/4]

template<typename _MatrixType, int _UpLo>

template<typename InputType >

Eigen::LLT< _MatrixType, _UpLo >::LLT ( const EigenBase< InputType > & matrix )

inlineexplicit

Definition at line 105 of file LLT.h.

◆ LLT() [4/4]

template<typename _MatrixType, int _UpLo>

template<typename InputType >

Eigen::LLT< _MatrixType, _UpLo >::LLT ( EigenBase< InputType > & matrix )

inlineexplicit

Constructs a LLT factorization from a given matrix.

This overloaded constructor is provided for inplace decomposition when MatrixType is a Eigen::Ref.

See also: LLT(const EigenBase&)

Definition at line 120 of file LLT.h.

Member Function Documentation

◆ _solve_impl()

template<typename _MatrixType , int _UpLo>

template<typename RhsType , typename DstType >

void Eigen::LLT< _MatrixType, _UpLo >::_solve_impl	(	const RhsType &	rhs,
		DstType &	dst
	)		const

Definition at line 485 of file LLT.h.

◆ _solve_impl_transposed()

template<typename _MatrixType , int _UpLo>

template<bool Conjugate, typename RhsType , typename DstType >

void Eigen::LLT< _MatrixType, _UpLo >::_solve_impl_transposed	(	const RhsType &	rhs,
		DstType &	dst
	)		const

Definition at line 492 of file LLT.h.

◆ adjoint()

template<typename _MatrixType, int _UpLo>

const LLT& Eigen::LLT< _MatrixType, _UpLo >::adjoint ( ) const

inline

Returns: the adjoint of *this, that is, a const reference to the decomposition itself as the underlying matrix is self-adjoint.

This method is provided for compatibility with other matrix decompositions, thus enabling generic code such as:

x = decomposition.adjoint().solve(b)

Definition at line 202 of file LLT.h.

◆ check_template_parameters()

template<typename _MatrixType, int _UpLo>

static void Eigen::LLT< _MatrixType, _UpLo >::check_template_parameters ( )

inlinestaticprotected

Definition at line 220 of file LLT.h.

◆ cols()

template<typename _MatrixType, int _UpLo>

EIGEN_CONSTEXPR Index Eigen::LLT< _MatrixType, _UpLo >::cols ( ) const

inline

Definition at line 205 of file LLT.h.

◆ compute() [1/2]

template<typename _MatrixType, int _UpLo>

template<typename InputType >

LLT& Eigen::LLT< _MatrixType, _UpLo >::compute ( const EigenBase< InputType > & matrix )

◆ compute() [2/2]

template<typename _MatrixType, int _UpLo>

template<typename InputType >

LLT<MatrixType,_UpLo>& Eigen::LLT< _MatrixType, _UpLo >::compute ( const EigenBase< InputType > & a )

Computes / recomputes the Cholesky decomposition A = LL^* = U^*U of matrix

Returns: a reference to *this

Example:

#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main()
{
   Matrix2f A, b;
   LLT<Matrix2f> llt;
   A << 2, -1, -1, 3;
   b << 1, 2, 3, 1;
   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the right hand side b:\n" << b << endl;
   cout << "Computing LLT decomposition..." << endl;
   llt.compute(A);
   cout << "The solution is:\n" << llt.solve(b) << endl;
   A(1,1)++;
   cout << "The matrix A is now:\n" << A << endl;
   cout << "Computing LLT decomposition..." << endl;
   llt.compute(A);
   cout << "The solution is now:\n" << llt.solve(b) << endl;
}

Output:

Definition at line 432 of file LLT.h.

◆ info()

template<typename _MatrixType, int _UpLo>

ComputationInfo Eigen::LLT< _MatrixType, _UpLo >::info ( ) const

inline

Reports whether previous computation was successful.

Returns: Success if computation was successful, NumericalIssue if the matrix.appears not to be positive definite.

Definition at line 191 of file LLT.h.

◆ matrixL()

template<typename _MatrixType, int _UpLo>

Traits::MatrixL Eigen::LLT< _MatrixType, _UpLo >::matrixL ( ) const

inline

Returns: a view of the lower triangular matrix L

Definition at line 135 of file LLT.h.

◆ matrixLLT()

template<typename _MatrixType, int _UpLo>

const MatrixType& Eigen::LLT< _MatrixType, _UpLo >::matrixLLT ( ) const

inline

Returns: the LLT decomposition matrix

TODO: document the storage layout

Definition at line 177 of file LLT.h.

◆ matrixU()

template<typename _MatrixType, int _UpLo>

Traits::MatrixU Eigen::LLT< _MatrixType, _UpLo >::matrixU ( ) const

inline

Returns: a view of the upper triangular matrix U

Definition at line 128 of file LLT.h.

◆ rankUpdate() [1/2]

template<typename _MatrixType, int _UpLo>

template<typename VectorType >

LLT& Eigen::LLT< _MatrixType, _UpLo >::rankUpdate	(	const VectorType &	vec,
		const RealScalar &	sigma = `1`
	)

◆ rankUpdate() [2/2]

template<typename _MatrixType, int _UpLo>

template<typename VectorType >

LLT<_MatrixType,_UpLo>& Eigen::LLT< _MatrixType, _UpLo >::rankUpdate	(	const VectorType &	v,
		const RealScalar &	sigma
	)

Performs a rank one update (or dowdate) of the current decomposition. If A = LL^* before the rank one update, then after it we have LL^* = A + sigma * v v^* where v must be a vector of same dimension.

Definition at line 469 of file LLT.h.

◆ rcond()

template<typename _MatrixType, int _UpLo>

RealScalar Eigen::LLT< _MatrixType, _UpLo >::rcond ( ) const

inline

Returns: an estimate of the reciprocal condition number of the matrix of which *this is the Cholesky decomposition.

Definition at line 166 of file LLT.h.

◆ reconstructedMatrix()

template<typename MatrixType , int _UpLo>

MatrixType Eigen::LLT< MatrixType, _UpLo >::reconstructedMatrix ( ) const

Returns: the matrix represented by the decomposition, i.e., it returns the product: L L^*. This function is provided for debug purpose.

Definition at line 528 of file LLT.h.

◆ rows()

template<typename _MatrixType, int _UpLo>

EIGEN_CONSTEXPR Index Eigen::LLT< _MatrixType, _UpLo >::rows ( ) const

inline

Definition at line 204 of file LLT.h.

◆ solveInPlace()

template<typename MatrixType , int _UpLo>

template<typename Derived >

void Eigen::LLT< MatrixType, _UpLo >::solveInPlace ( const MatrixBase< Derived > & bAndX ) const

Definition at line 516 of file LLT.h.

Friends And Related Function Documentation

◆ SolverBase< LLT >

template<typename _MatrixType, int _UpLo>

friend class SolverBase< LLT >

friend

Definition at line 72 of file LLT.h.

Member Data Documentation

◆ m_info

template<typename _MatrixType, int _UpLo>

ComputationInfo Eigen::LLT< _MatrixType, _UpLo >::m_info

protected

Definition at line 232 of file LLT.h.

◆ m_isInitialized

template<typename _MatrixType, int _UpLo>

bool Eigen::LLT< _MatrixType, _UpLo >::m_isInitialized

protected

Definition at line 231 of file LLT.h.

◆ m_l1_norm

template<typename _MatrixType, int _UpLo>

RealScalar Eigen::LLT< _MatrixType, _UpLo >::m_l1_norm

protected

Definition at line 230 of file LLT.h.

◆ m_matrix

template<typename _MatrixType, int _UpLo>

MatrixType Eigen::LLT< _MatrixType, _UpLo >::m_matrix

protected

Definition at line 229 of file LLT.h.

The documentation for this class was generated from the following file:

LLT.h

Public Types

Public Member Functions

Static Protected Member Functions

Protected Attributes

Friends

Additional Inherited Members

Detailed Description

template<typename _MatrixType, int _UpLo> class Eigen::LLT< _MatrixType, _UpLo >

Member Typedef Documentation

◆ Base

◆ MatrixType

◆ Traits

Member Enumeration Documentation

◆ anonymous enum

◆ anonymous enum

Constructor & Destructor Documentation

◆ LLT() [1/4]

◆ LLT() [2/4]

◆ LLT() [3/4]

◆ LLT() [4/4]

Member Function Documentation

◆ _solve_impl()

◆ _solve_impl_transposed()

◆ adjoint()

◆ check_template_parameters()

◆ cols()

◆ compute() [1/2]

◆ compute() [2/2]

◆ info()

◆ matrixL()

◆ matrixLLT()

◆ matrixU()

◆ rankUpdate() [1/2]

◆ rankUpdate() [2/2]

◆ rcond()

◆ reconstructedMatrix()

◆ rows()

◆ solveInPlace()

Friends And Related Function Documentation

◆ SolverBase< LLT >

Member Data Documentation

◆ m_info

◆ m_isInitialized

◆ m_l1_norm

◆ m_matrix

template<typename _MatrixType, int _UpLo>
class Eigen::LLT< _MatrixType, _UpLo >