Table of Contents
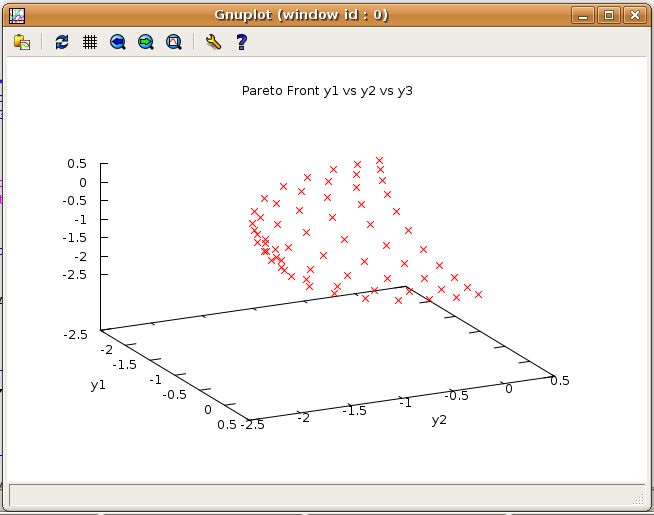
This tutorial explains how to solve static optimization problems with three objectives.
Mathematical formulation
For the static tri-objective problem only three scalar variables are involved: y1 , y2 and y3 . The aim is to simultaneously minimize these three variables. However, all are bounded and have to satisfy a nonlinear constraint.
An ACADO tutorial code
The following piece of code illustrates how to set up the tri-objective optimization problem mentioned above. The Pareto set is generated based on WS. The number of Pareto points np between two indidivual objectives is set to 11. Hence, this results in 1/2* np *( np +1) = 66 single objective optimization problems to be solved and also in 66 points on the global Pareto front. This code is available in the examples/multi_objective directory as scalar3_ws.cpp. The NBI and NNC version are called scalar3_nbi.cpp and scalar3_nnc.cpp, respectively.
#include <acado_optimal_control.hpp>
#include <include/acado_gnuplot/gnuplot_window.hpp>
int main( )
{
// INTRODUCE THE VARIABLES:
// -------------------------
Parameter y1,y2,y3;
// DEFINE AN OPTIMIZATION PROBLEM:
// -------------------------------
NLP nlp;
nlp.minimize( 0, y1 );
nlp.minimize( 1, y2 );
nlp.minimize( 2, y3 );
nlp.subjectTo( -5.0 <= y1 <= 5.0 );
nlp.subjectTo( -5.0 <= y2 <= 5.0 );
nlp.subjectTo( -5.0 <= y3 <= 5.0 );
nlp.subjectTo( y1*y1+y2*y2+y3*y3 <= 4.0 );
// DEFINE A MULTI-OBJECTIVE ALGORITHM AND SOLVE THE NLP:
// -----------------------------------------------------
MultiObjectiveAlgorithm algorithm(nlp);
algorithm.set( PARETO_FRONT_GENERATION, PFG_WEIGHTED_SUM );
algorithm.set( PARETO_FRONT_DISCRETIZATION, 11 );
// Generate Pareto set
algorithm.solve();
algorithm.getWeights("scalar3_ws_weights.txt");
// GET THE RESULT FOR THE PARETO FRONT AND PLOT IT:
// ------------------------------------------------
VariablesGrid paretoFront;
algorithm.getParetoFront( paretoFront );
paretoFront.print();
GnuplotWindow window;
window.addSubplot3D( paretoFront, "Pareto Front y1 vs y2 vs y3",
window.plot( );
FILE *file = fopen("scalar3_ws_pareto.txt","w");
paretoFront.print();
file << paretoFront;
fclose(file);
// PRINT INFORMATION ABOUT THE ALGORITHM:
// --------------------------------------
algorithm.printInfo();
return 0;
}
ACADO results
The corresponding Pareto surface as returned by WS looks as follows in GNUplot. Note however that it not possible to visualize Pareto fronts for more than three objectives in ACADO.
ACADO results
The resulting Pareto set is stored in a separate file scalar3_ws_pareto.txt. These output files can be generated for optimization problems with any number of objectives.
-6.0339247444016197e-10 -1.8204124581840835e-19 -2.0000000000004419e+00
+4.3410001958593765e-18 -2.2086305372928050e-01 -1.9877674691748790e+00
-1.1928741869326143e-25 -4.8507125721930250e-01 -1.9402849985314583e+00
+1.0688203722972674e-32 -7.8783862345177114e-01 -1.8382900489498144e+00
-2.3599998872151069e-39 -1.1094004597228548e+00 -1.6641005446192576e+00
+8.4884318705147905e-46 -1.4142136630774804e+00 -1.4142134635633234e+00
-3.0725609253436269e-52 -1.6641006664448956e+00 -1.1094002780240186e+00
-3.0725609253436269e-52 -1.8382900903529757e+00 -7.8783852773405350e-01
-3.0725609253436269e-52 -1.9402850066539299e+00 -4.8507122508548900e-01
-3.0725609253436269e-52 -1.9877674700672645e+00 -2.2086304581002328e-01
-3.0725609253436269e-52 -2.0000000000015881e+00 +1.3235897780355596e-09
-2.2086305216533414e-01 -5.9347722266081537e-10 -1.9877674694880068e+00
-2.4618298236569022e-01 -2.4618298618583043e-01 -1.9694638551053811e+00
-2.7216552862893106e-01 -5.4433107490727173e-01 -1.9051586827531084e+00
-2.9488391670532416e-01 -8.8465181554231753e-01 -1.7693034348056000e+00
-3.0860670425920550e-01 -1.2344269797406133e+00 -1.5430333585922362e+00
-3.0860669519518702e-01 -1.5430337031369126e+00 -1.2344265536197696e+00
-2.9488390199898806e-01 -1.7693035758072075e+00 -8.8465154218368436e-01
-2.7216552100640273e-01 -1.9051587124381759e+00 -5.4433097661944851e-01
-2.4618298014230572e-01 -1.9694638583633912e+00 -2.4618296291736100e-01
-2.2086305175526319e-01 -1.9877674693992098e+00 +3.6018412987413873e-09
-4.8506817776484890e-01 -5.9545384492078191e-07 -1.9402857709655916e+00
-5.4433105623755507e-01 -2.7216553832091156e-01 -1.9051586866287347e+00
-6.0302269829115662e-01 -6.0302274749212481e-01 -1.8090680456725017e+00
-6.4888570402525780e-01 -9.7332873025584588e-01 -1.6222140858451850e+00
-6.6666666973557254e-01 -1.3333337000141567e+00 -1.3333329789281336e+00
-6.4888564897503143e-01 -1.6222144861592278e+00 -9.7332810974089889e-01
-6.0302265782917475e-01 -1.8090681503835460e+00 -6.0302248093315258e-01
-5.4433104313685432e-01 -1.9051587001555903e+00 -2.7216547239182698e-01
-4.8507124776010019e-01 -1.9402850009085908e+00 +9.8681901959836449e-09
-7.8785246523567187e-01 -3.5769621710396438e-05 -1.8382843011505723e+00
-8.8465174548749637e-01 -2.9488394104942406e-01 -1.7693034650882984e+00
-9.7332855583553524e-01 -6.4888582204517120e-01 -1.6222141415710765e+00
-1.0289915466186226e+00 -1.0289918968912204e+00 -1.3719883785522315e+00
-1.0289914721387488e+00 -1.3719891570135585e+00 -1.0289909446435210e+00
-9.7332844608109381e-01 -1.6222144338251989e+00 -6.4888527369735249e-01
-8.8465169846312341e-01 -1.7693035170009492e+00 -2.9488377941300475e-01
-7.8783858793812989e-01 -1.8382900641627584e+00 +2.5640455421404099e-08
-1.1093847017857583e+00 +2.0862253922926920e-05 -1.6641111698321347e+00
-1.2344268214046252e+00 -3.0860676108397916e-01 -1.5430334710202951e+00
-1.3333333827927383e+00 -6.6666689983804706e-01 -1.3333331743510604e+00
-1.3719886898392557e+00 -1.0289919652975361e+00 -1.0289910694613480e+00
-1.3333332404604765e+00 -1.3333336932253486e+00 -6.6666616746536644e-01
-1.2344267209485447e+00 -1.5430336137835836e+00 -3.0860646763923405e-01
-1.1094003669188477e+00 -1.6641006063043113e+00 +5.5926040158941689e-08
-1.4142126252363287e+00 +2.8170134986627016e-06 -1.4142145032453608e+00
-1.5430335318359385e+00 -3.0860679361429155e-01 -1.2344267382219369e+00
-1.6222142464421061e+00 -6.4888593355435087e-01 -9.7332831288775490e-01
-1.6222141731171174e+00 -9.7332884327443447e-01 -6.4888532984268288e-01
-1.5430334180518939e+00 -1.2344269722976349e+00 -3.0860644575425905e-01
-1.4142135191429959e+00 -1.4142136069870161e+00 +8.7844020309115617e-08
-1.6641005935099231e+00 -1.4852620071445673e-08 -1.1094003857715344e+00
-1.7693034985481642e+00 -2.9488400662962538e-01 -8.8465165906914933e-01
-1.8090680700811970e+00 -6.0302285577941128e-01 -6.0302252427472047e-01
-1.7693034328442017e+00 -8.8465188266528616e-01 -2.9488373923084860e-01
-1.6641005478191604e+00 -1.1094004555793047e+00 +9.0366530969103465e-08
-1.8382900880816442e+00 +1.0757941791084483e-08 -7.8783861609366790e-01
-1.9051586975842958e+00 -2.7216559068175072e-01 -5.4433099399723428e-01
-1.9051586792054536e+00 -5.4433113231906594e-01 -2.7216544448327151e-01
-1.8382900380464486e+00 -7.8783864996039943e-01 +6.2226207166388506e-08
-1.9402855324666246e+00 -3.8631604795599794e-06 -4.8506912960624948e-01
-1.9694638558941060e+00 -2.4618301393884950e-01 -2.4618295003446505e-01
-1.9402849930103772e+00 -4.8507128006532052e-01 +3.1812726030084129e-08
-1.9877674288313747e+00 +9.5123026565193530e-07 -2.2086347041697243e-01
-1.9877674679136375e+00 -2.2086306555009402e-01 +1.3559657430738115e-08
-2.0000000000015756e+00 +1.3235906295679459e-09 -8.1260465489160793e-17
Next example: Optimal control of a plug flow reactor with conflicting energy and conversion objectives