MatrixBase< Derived > Class Template Reference

Base class for all matrices, vectors, and expressions. More...

#include <MatrixBase.h>

Inheritance diagram for MatrixBase< Derived >:
Inheritance graph
[legend]

List of all members.

Classes

class  InnerIterator

Public Types

enum  {
  RowsAtCompileTime = ei_traits<Derived>::RowsAtCompileTime, ColsAtCompileTime = ei_traits<Derived>::ColsAtCompileTime, SizeAtCompileTime, MaxRowsAtCompileTime = ei_traits<Derived>::MaxRowsAtCompileTime,
  MaxColsAtCompileTime = ei_traits<Derived>::MaxColsAtCompileTime, MaxSizeAtCompileTime, IsVectorAtCompileTime, Flags = ei_traits<Derived>::Flags,
  CoeffReadCost = ei_traits<Derived>::CoeffReadCost
}
typedef Eigen::Transpose
< NestByValue< typename
ei_cleantype
< ConjugateReturnType >::type > > 		AdjointReturnType
typedef Block< CwiseNullaryOp
< ei_scalar_identity_op
< Scalar >, SquareMatrixType >
, ei_traits< Derived >
::RowsAtCompileTime, ei_traits
< Derived >::ColsAtCompileTime > 		BasisReturnType
typedef Block< Derived,
ei_traits< Derived >
::RowsAtCompileTime, 1 > 		ColXpr
typedef ei_meta_if< NumTraits
< Scalar >::IsComplex, const
CwiseUnaryOp
< ei_scalar_conjugate_op
< Scalar >, Derived >, const
Derived & >::ret 		ConjugateReturnType
typedef CwiseNullaryOp
< ei_scalar_constant_op
< Scalar >, Derived > 		ConstantReturnType
typedef Matrix< typename
NumTraits< typename ei_traits
< Derived >::Scalar >::Real,
ei_traits< Derived >
::ColsAtCompileTime, 1 > 		EigenvaluesReturnType
typedef CwiseNullaryOp
< ei_scalar_identity_op
< Scalar >, Derived > 		IdentityReturnType
typedef CwiseUnaryOp
< ei_scalar_imag_op< Scalar >
, Derived > 		ImagReturnType
typedef ei_packet_traits
< Scalar >::type 		PacketScalar
typedef ei_plain_matrix_type
< Derived >::type 		PlainMatrixType
typedef ei_plain_matrix_type
< Derived >::type 		PlainMatrixType_ColMajor
typedef CwiseUnaryOp
< ei_scalar_real_op< Scalar >
, Derived > 		RealReturnType
typedef NumTraits< Scalar >::Real RealScalar
typedef Block< Derived,
1, ei_traits< Derived >
::ColsAtCompileTime > 		RowXpr
typedef ei_traits< Derived >
::Scalar 		Scalar
typedef CwiseUnaryOp
< ei_scalar_multiple_op
< Scalar >, Derived > 		ScalarMultipleReturnType
typedef CwiseUnaryOp
< ei_scalar_quotient1_op
< Scalar >, Derived > 		ScalarQuotient1ReturnType
typedef Matrix< Scalar,
EIGEN_ENUM_MAX(RowsAtCompileTime,
ColsAtCompileTime),
EIGEN_ENUM_MAX(RowsAtCompileTime,
ColsAtCompileTime)> 		SquareMatrixType

Public Member Functions

const AdjointReturnType adjoint () const
bool all (void) const
bool any (void) const
const DiagonalMatrix< Derived > asDiagonal () const
template<typename CustomBinaryOp , typename OtherDerived >
const CwiseBinaryOp
< CustomBinaryOp, Derived,
OtherDerived > 		binaryExpr (const MatrixBase< OtherDerived > &other, const CustomBinaryOp &func=CustomBinaryOp()) const
template<int BlockRows, int BlockCols>
const BlockReturnType< Derived,
BlockRows, BlockCols >::Type 		block (int startRow, int startCol) const
template<int BlockRows, int BlockCols>
BlockReturnType< Derived,
BlockRows, BlockCols >::Type 		block (int startRow, int startCol)
const BlockReturnType< Derived >
::Type 		block (int startRow, int startCol, int blockRows, int blockCols) const
BlockReturnType< Derived >::Type block (int startRow, int startCol, int blockRows, int blockCols)
template<typename NewType >
const CwiseUnaryOp
< ei_scalar_cast_op< typename
ei_traits< Derived >::Scalar,
NewType >, Derived > 		cast () const
const Scalar coeff (int index) const
const Scalar coeff (int row, int col) const
Scalar & coeffRef (int index)
Scalar & coeffRef (int row, int col)
const ColXpr col (int i) const
ColXpr col (int i)
int cols () const
const PartialRedux< Derived,
Vertical > 		colwise () const
template<typename OtherDerived >
void computeInverse (MatrixBase< OtherDerived > *result) const
template<typename ResultType >
void computeInverse (MatrixBase< ResultType > *result) const
ConjugateReturnType conjugate () const
Derived & const_cast_derived () const
template<typename OtherDerived >
void copyCoeff (int index, const MatrixBase< OtherDerived > &other)
template<typename OtherDerived >
void copyCoeff (int row, int col, const MatrixBase< OtherDerived > &other)
template<typename OtherDerived , int StoreMode, int LoadMode>
void copyPacket (int index, const MatrixBase< OtherDerived > &other)
template<typename OtherDerived , int StoreMode, int LoadMode>
void copyPacket (int row, int col, const MatrixBase< OtherDerived > &other)
template<int CRows, int CCols>
const BlockReturnType< Derived,
CRows, CCols >::Type 		corner (CornerType type) const
template<int CRows, int CCols>
BlockReturnType< Derived,
CRows, CCols >::Type 		corner (CornerType type)
const BlockReturnType< Derived >
::Type 		corner (CornerType type, int cRows, int cCols) const
BlockReturnType< Derived >::Type corner (CornerType type, int cRows, int cCols)
int count () const
template<typename OtherDerived >
PlainMatrixType cross (const MatrixBase< OtherDerived > &other) const
Cwise< Derived > cwise ()
const Cwise< Derived > cwise () const
Derived & derived ()
const Derived & derived () const
Scalar determinant () const
const DiagonalCoeffs< Derived > diagonal () const
DiagonalCoeffs< Derived > diagonal ()
template<typename OtherDerived >
Scalar dot (const MatrixBase< OtherDerived > &other) const
EigenvaluesReturnType eigenvalues () const
template<int Size>
const BlockReturnType< Derived,
Size >::SubVectorType 		end () const
template<int Size>
BlockReturnType< Derived, Size >
::SubVectorType 		end ()
const BlockReturnType< Derived,
Dynamic >::SubVectorType 		end (int size) const
BlockReturnType< Derived,
Dynamic >::SubVectorType 		end (int size)
Matrix< Scalar, 3, 1 > eulerAngles (int a0, int a1, int a2) const
EIGEN_STRONG_INLINE const
ei_eval< Derived >::type 		eval () const
void fill (const Scalar &value)
const WithFormat< Derived > format (const IOFormat &fmt) const
const ImagReturnType imag () const
int innerSize () const
const PlainMatrixType inverse () const
template<typename OtherDerived >
bool isApprox (const MatrixBase< OtherDerived > &other, typename NumTraits< Scalar >::Real prec) const
template<typename OtherDerived >
bool isApprox (const MatrixBase< OtherDerived > &other, RealScalar prec=precision< Scalar >()) const
bool isApproxToConstant (const Scalar &value, RealScalar prec=precision< Scalar >()) const
bool isConstant (const Scalar &value, RealScalar prec=precision< Scalar >()) const
bool isDiagonal (RealScalar prec=precision< Scalar >()) const
bool isIdentity (RealScalar prec=precision< Scalar >()) const
bool isLowerTriangular (RealScalar prec=precision< Scalar >()) const
template<typename OtherDerived >
bool isMuchSmallerThan (const MatrixBase< OtherDerived > &other, typename NumTraits< Scalar >::Real prec) const
template<typename Derived >
bool isMuchSmallerThan (const typename NumTraits< Scalar >::Real &other, typename NumTraits< Scalar >::Real prec) const
template<typename OtherDerived >
bool isMuchSmallerThan (const MatrixBase< OtherDerived > &other, RealScalar prec=precision< Scalar >()) const
bool isMuchSmallerThan (const RealScalar &other, RealScalar prec=precision< Scalar >()) const
bool isOnes (RealScalar prec=precision< Scalar >()) const
template<typename OtherDerived >
bool isOrthogonal (const MatrixBase< OtherDerived > &other, RealScalar prec=precision< Scalar >()) const
bool isUnitary (RealScalar prec=precision< Scalar >()) const
bool isUpperTriangular (RealScalar prec=precision< Scalar >()) const
bool isVector () const
bool isZero (RealScalar prec=precision< Scalar >()) const
const Flagged< Derived,
0, EvalBeforeNestingBit|EvalBeforeAssigningBit > 		lazy () const
template<typename Lhs , typename Rhs >
Derived & lazyAssign (const SparseProduct< Lhs, Rhs, DenseTimeSparseProduct > &product)
template<typename Lhs , typename Rhs >
Derived & lazyAssign (const SparseProduct< Lhs, Rhs, SparseTimeDenseProduct > &product)
template<typename Derived1 , typename Derived2 >
Derived & lazyAssign (const SparseProduct< Derived1, Derived2, DenseTimeSparseProduct > &product)
template<typename Derived1 , typename Derived2 >
Derived & lazyAssign (const SparseProduct< Derived1, Derived2, SparseTimeDenseProduct > &product)
template<typename OtherDerived >
Derived & lazyAssign (const Flagged< OtherDerived, 0, EvalBeforeNestingBit|EvalBeforeAssigningBit > &other)
template<typename Lhs , typename Rhs >
Derived & lazyAssign (const Product< Lhs, Rhs, CacheFriendlyProduct > &product)
template<typename OtherDerived >
Derived & lazyAssign (const MatrixBase< OtherDerived > &other)
const LDLT< PlainMatrixType > ldlt () const
const LLT< PlainMatrixType > llt () const
template<int p>
RealScalar lpNorm () const
const LU< PlainMatrixType > lu () const
template<unsigned int Added>
const Flagged< Derived, Added, 0 > marked () const
ei_traits< Derived >::Scalar maxCoeff (int *index) const
ei_traits< Derived >::Scalar maxCoeff (int *row, int *col) const
ei_traits< Derived >::Scalar maxCoeff () const
ei_traits< Derived >::Scalar minCoeff (int *index) const
ei_traits< Derived >::Scalar minCoeff (int *row, int *col) const
ei_traits< Derived >::Scalar minCoeff () const
const Minor< Derived > minor (int row, int col) const
Minor< Derived > minor (int row, int col)
const NestByValue< Derived > nestByValue () const
int nonZeros () const
RealScalar norm () const
void normalize ()
const PlainMatrixType normalized () const
template<typename OtherDerived >
bool operator!= (const MatrixBase< OtherDerived > &other) const
Scalar & operator() (int index)
const Scalar operator() (int index) const
Scalar & operator() (int row, int col)
const Scalar operator() (int row, int col) const
template<typename OtherDerived >
const ProductReturnType
< Derived, OtherDerived >
::Type 		operator* (const MatrixBase< OtherDerived > &other) const
const ScalarMultipleReturnType operator* (const Scalar &scalar) const
template<typename OtherDerived >
Derived & operator*= (const MatrixBase< OtherDerived > &other)
Derived & operator*= (const Scalar &other)
template<typename OtherDerived >
const CwiseBinaryOp
< ei_scalar_sum_op< typename
ei_traits< Derived >::Scalar >
, Derived, OtherDerived > 		operator+ (const MatrixBase< OtherDerived > &other) const
template<typename Lhs , typename Rhs >
Derived & operator+= (const Flagged< Product< Lhs, Rhs, CacheFriendlyProduct >, 0, EvalBeforeNestingBit|EvalBeforeAssigningBit > &other)
template<typename OtherDerived >
Derived & operator+= (const MatrixBase< OtherDerived > &other)
template<typename OtherDerived >
const CwiseBinaryOp
< ei_scalar_difference_op
< typename ei_traits< Derived >
::Scalar >, Derived,
OtherDerived > 		operator- (const MatrixBase< OtherDerived > &other) const
const CwiseUnaryOp
< ei_scalar_opposite_op
< typename ei_traits< Derived >
::Scalar >, Derived > 		operator- () const
template<typename OtherDerived >
Derived & operator-= (const MatrixBase< OtherDerived > &other)
const CwiseUnaryOp
< ei_scalar_quotient1_op
< typename ei_traits< Derived >
::Scalar >, Derived > 		operator/ (const Scalar &scalar) const
Derived & operator/= (const Scalar &other)
template<typename OtherDerived >
CommaInitializer< Derived > operator<< (const MatrixBase< OtherDerived > &other)
CommaInitializer< Derived > operator<< (const Scalar &s)
Derived & operator= (const MatrixBase &other)
template<typename OtherDerived >
Derived & operator= (const MatrixBase< OtherDerived > &other)
template<typename OtherDerived >
bool operator== (const MatrixBase< OtherDerived > &other) const
Scalar & operator[] (int index)
const Scalar operator[] (int index) const
RealScalar operatorNorm () const
int outerSize () const
template<int LoadMode>
PacketScalar packet (int index) const
template<int LoadMode>
PacketScalar packet (int row, int col) const
template<unsigned int Mode>
const Part< Derived, Mode > part () const
template<unsigned int Mode>
Part< Derived, Mode > part ()
const QR< PlainMatrixType > qr () const
const RealReturnType real () const
const RowXpr row (int i) const
RowXpr row (int i)
int rows () const
const PartialRedux< Derived,
Horizontal > 		rowwise () const
template<int Size>
const BlockReturnType< Derived,
Size >::SubVectorType 		segment (int start) const
template<int Size>
BlockReturnType< Derived, Size >
::SubVectorType 		segment (int start)
const BlockReturnType< Derived >
::SubVectorType 		segment (int start, int size) const
BlockReturnType< Derived >
::SubVectorType 		segment (int start, int size)
template<typename ElseDerived >
const Select< Derived,
NestByValue< typename
ElseDerived::ConstantReturnType >
, ElseDerived > 		select (typename ElseDerived::Scalar thenScalar, const MatrixBase< ElseDerived > &elseMatrix) const
template<typename ThenDerived >
const Select< Derived,
ThenDerived, NestByValue
< typename
ThenDerived::ConstantReturnType > > 		select (const MatrixBase< ThenDerived > &thenMatrix, typename ThenDerived::Scalar elseScalar) const
template<typename ThenDerived , typename ElseDerived >
const Select< Derived,
ThenDerived, ElseDerived > 		select (const MatrixBase< ThenDerived > &thenMatrix, const MatrixBase< ElseDerived > &elseMatrix) const
Derived & setConstant (const Scalar &value)
Derived & setIdentity ()
Derived & setOnes ()
Derived & setRandom ()
Derived & setZero ()
int size () const
template<typename OtherDerived >
ei_plain_matrix_type_column_major
< OtherDerived >::type 		solveTriangular (const MatrixBase< OtherDerived > &other) const
template<typename OtherDerived >
void solveTriangularInPlace (const MatrixBase< OtherDerived > &other) const
RealScalar squaredNorm () const
template<int Size>
const BlockReturnType< Derived,
Size >::SubVectorType 		start () const
template<int Size>
BlockReturnType< Derived, Size >
::SubVectorType 		start (void)
const BlockReturnType< Derived,
Dynamic >::SubVectorType 		start (int size) const
BlockReturnType< Derived,
Dynamic >::SubVectorType 		start (int size)
int stride (void) const
Scalar sum () const
SVD< PlainMatrixType > svd () const
template<typename OtherDerived >
void swap (const MatrixBase< OtherDerived > &other)
Scalar trace () const
const Eigen::Transpose< Derived > transpose () const
Eigen::Transpose< Derived > transpose ()
void transposeInPlace ()
template<typename CustomUnaryOp >
const CwiseUnaryOp
< CustomUnaryOp, Derived > 		unaryExpr (const CustomUnaryOp &func=CustomUnaryOp()) const
PlainMatrixType unitOrthogonal (void) const
template<typename Visitor >
void visit (Visitor &func) const
Scalar & w ()
const Scalar w () const
template<int StoreMode>
EIGEN_STRONG_INLINE void writePacket (int index, const typename ei_packet_traits< typename ei_traits< Derived >::Scalar >::type &x)
template<int StoreMode>
EIGEN_STRONG_INLINE void writePacket (int row, int col, const typename ei_packet_traits< typename ei_traits< Derived >::Scalar >::type &x)
template<int StoreMode>
void writePacket (int index, const PacketScalar &x)
template<int StoreMode>
void writePacket (int row, int col, const PacketScalar &x)
Scalar & x ()
const Scalar x () const
Scalar & y ()
const Scalar y () const
Scalar & z ()
const Scalar z () const

Static Public Member Functions

static const ConstantReturnType Constant (const Scalar &value)
static const ConstantReturnType Constant (int size, const Scalar &value)
static const ConstantReturnType Constant (int rows, int cols, const Scalar &value)
static const IdentityReturnType Identity (int rows, int cols)
static const IdentityReturnType Identity ()
template<typename CustomNullaryOp >
static const CwiseNullaryOp
< CustomNullaryOp, Derived > 		NullaryExpr (const CustomNullaryOp &func)
template<typename CustomNullaryOp >
static const CwiseNullaryOp
< CustomNullaryOp, Derived > 		NullaryExpr (int size, const CustomNullaryOp &func)
template<typename CustomNullaryOp >
static const CwiseNullaryOp
< CustomNullaryOp, Derived > 		NullaryExpr (int rows, int cols, const CustomNullaryOp &func)
static const ConstantReturnType Ones ()
static const ConstantReturnType Ones (int size)
static const ConstantReturnType Ones (int rows, int cols)
static const CwiseNullaryOp
< ei_scalar_random_op< Scalar >
, Derived > 		Random ()
static const CwiseNullaryOp
< ei_scalar_random_op< Scalar >
, Derived > 		Random (int size)
static const CwiseNullaryOp
< ei_scalar_random_op< Scalar >
, Derived > 		Random (int rows, int cols)
static const BasisReturnType Unit (int i)
static const BasisReturnType Unit (int size, int i)
static const BasisReturnType UnitW ()
static const BasisReturnType UnitX ()
static const BasisReturnType UnitY ()
static const BasisReturnType UnitZ ()
static const ConstantReturnType Zero ()
static const ConstantReturnType Zero (int size)
static const ConstantReturnType Zero (int rows, int cols)

Protected Member Functions

 MatrixBase ()

Private Member Functions

template<typename OtherDerived >
 MatrixBase (const MatrixBase< OtherDerived > &)
 MatrixBase (int, int)
 MatrixBase (int)

Friends

const CwiseUnaryOp
< ei_scalar_multiple_op
< typename ei_traits< Derived >
::Scalar >, Derived > 		operator* (const Scalar &scalar, const MatrixBase &matrix)

Related Functions

(Note that these are not member functions.)



template<typename Derived >
std::ostream & operator<< (std::ostream &s, const MatrixBase< Derived > &m)

Detailed Description

template<typename Derived>
class MatrixBase< Derived >

Base class for all matrices, vectors, and expressions.

This class is the base that is inherited by all matrix, vector, and expression types. Most of the Eigen API is contained in this class. Other important classes for the Eigen API are Matrix, Cwise, and PartialRedux.

Note that some methods are defined in the Array module.

Parameters:
Derived is the derived type, e.g. a matrix type, or an expression, etc.

When writing a function taking Eigen objects as argument, if you want your function to take as argument any matrix, vector, or expression, just let it take a MatrixBase argument. As an example, here is a function printFirstRow which, given a matrix, vector, or expression x, prints the first row of x.

    template<typename Derived>
    void printFirstRow(const Eigen::MatrixBase<Derived>& x)
    {
      cout << x.row(0) << endl;
    }

Definition at line 55 of file MatrixBase.h.

Member Typedef Documentation

template<typename Derived>
typedef Eigen::Transpose<NestByValue<typename ei_cleantype<ConjugateReturnType>::type> > MatrixBase< Derived >::AdjointReturnType

Definition at line 206 of file MatrixBase.h.

template<typename Derived>
typedef Block<CwiseNullaryOp<ei_scalar_identity_op<Scalar>, SquareMatrixType>, ei_traits<Derived>::RowsAtCompileTime, ei_traits<Derived>::ColsAtCompileTime> MatrixBase< Derived >::BasisReturnType

Definition at line 218 of file MatrixBase.h.

template<typename Derived>
typedef Block<Derived, ei_traits<Derived>::RowsAtCompileTime, 1> MatrixBase< Derived >::ColXpr

Definition at line 210 of file MatrixBase.h.

template<typename Derived>
typedef ei_meta_if<NumTraits<Scalar>::IsComplex, const CwiseUnaryOp<ei_scalar_conjugate_op<Scalar>, Derived>, const Derived& >::ret MatrixBase< Derived >::ConjugateReturnType

Definition at line 199 of file MatrixBase.h.

template<typename Derived>
typedef CwiseNullaryOp<ei_scalar_constant_op<Scalar>,Derived> MatrixBase< Derived >::ConstantReturnType

Definition at line 190 of file MatrixBase.h.

template<typename Derived>
typedef Matrix<typename NumTraits<typename ei_traits<Derived>::Scalar>::Real, ei_traits<Derived>::ColsAtCompileTime, 1> MatrixBase< Derived >::EigenvaluesReturnType

Definition at line 208 of file MatrixBase.h.

template<typename Derived>
typedef CwiseNullaryOp<ei_scalar_identity_op<Scalar>,Derived> MatrixBase< Derived >::IdentityReturnType

Definition at line 214 of file MatrixBase.h.

template<typename Derived>
typedef CwiseUnaryOp<ei_scalar_imag_op<Scalar>, Derived> MatrixBase< Derived >::ImagReturnType

Definition at line 203 of file MatrixBase.h.

template<typename Derived>
typedef ei_packet_traits<Scalar>::type MatrixBase< Derived >::PacketScalar

Reimplemented in MapBase< Derived >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, and MapBase< Map< MatrixType, PacketAccess > >.

Definition at line 63 of file MatrixBase.h.

template<typename Derived>
typedef ei_plain_matrix_type<Derived>::type MatrixBase< Derived >::PlainMatrixType

Definition at line 181 of file MatrixBase.h.

template<typename Derived>
typedef ei_plain_matrix_type<Derived>::type MatrixBase< Derived >::PlainMatrixType_ColMajor

Definition at line 187 of file MatrixBase.h.

template<typename Derived>
typedef CwiseUnaryOp<ei_scalar_real_op<Scalar>, Derived> MatrixBase< Derived >::RealReturnType

Definition at line 201 of file MatrixBase.h.

template<typename Derived>
typedef NumTraits<Scalar>::Real MatrixBase< Derived >::RealScalar

This is the "real scalar" type; if the Scalar type is already real numbers (e.g. int, float or double) then RealScalar is just the same as Scalar. If Scalar is std::complex<T> then RealScalar is T.

See also:
class NumTraits

Definition at line 146 of file MatrixBase.h.

template<typename Derived>
typedef Block<Derived, 1, ei_traits<Derived>::ColsAtCompileTime> MatrixBase< Derived >::RowXpr

Definition at line 212 of file MatrixBase.h.

template<typename Derived>
typedef ei_traits<Derived>::Scalar MatrixBase< Derived >::Scalar

Reimplemented in MapBase< Derived >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, and MapBase< Map< MatrixType, PacketAccess > >.

Definition at line 60 of file MatrixBase.h.

template<typename Derived>
typedef CwiseUnaryOp<ei_scalar_multiple_op<Scalar>, Derived> MatrixBase< Derived >::ScalarMultipleReturnType

Definition at line 192 of file MatrixBase.h.

template<typename Derived>
typedef CwiseUnaryOp<ei_scalar_quotient1_op<Scalar>, Derived> MatrixBase< Derived >::ScalarQuotient1ReturnType

Definition at line 194 of file MatrixBase.h.

template<typename Derived>
typedef Matrix<Scalar,EIGEN_ENUM_MAX(RowsAtCompileTime,ColsAtCompileTime), EIGEN_ENUM_MAX(RowsAtCompileTime,ColsAtCompileTime)> MatrixBase< Derived >::SquareMatrixType

type of the equivalent square matrix

Definition at line 150 of file MatrixBase.h.

Member Enumeration Documentation

template<typename Derived>
anonymous enum
Enumerator:
RowsAtCompileTime 

The number of rows at compile-time. This is just a copy of the value provided by the Derived type. If a value is not known at compile-time, it is set to the Dynamic constant.

See also:
MatrixBase::rows(), MatrixBase::cols(), ColsAtCompileTime, SizeAtCompileTime
ColsAtCompileTime 

The number of columns at compile-time. This is just a copy of the value provided by the Derived type. If a value is not known at compile-time, it is set to the Dynamic constant.

See also:
MatrixBase::rows(), MatrixBase::cols(), RowsAtCompileTime, SizeAtCompileTime
SizeAtCompileTime 

This is equal to the number of coefficients, i.e. the number of rows times the number of columns, or to Dynamic if this is not known at compile-time.

See also:
RowsAtCompileTime, ColsAtCompileTime
MaxRowsAtCompileTime 

This value is equal to the maximum possible number of rows that this expression might have. If this expression might have an arbitrarily high number of rows, this value is set to Dynamic.

This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation.

See also:
RowsAtCompileTime, MaxColsAtCompileTime, MaxSizeAtCompileTime
MaxColsAtCompileTime 

This value is equal to the maximum possible number of columns that this expression might have. If this expression might have an arbitrarily high number of columns, this value is set to Dynamic.

This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation.

See also:
ColsAtCompileTime, MaxRowsAtCompileTime, MaxSizeAtCompileTime
MaxSizeAtCompileTime 

This value is equal to the maximum possible number of coefficients that this expression might have. If this expression might have an arbitrarily high number of coefficients, this value is set to Dynamic.

This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation.

See also:
SizeAtCompileTime, MaxRowsAtCompileTime, MaxColsAtCompileTime
IsVectorAtCompileTime 

This is set to true if either the number of rows or the number of columns is known at compile-time to be equal to 1. Indeed, in that case, we are dealing with a column-vector (if there is only one column) or with a row-vector (if there is only one row).

Flags 

This stores expression flags flags which may or may not be inherited by new expressions constructed from this one. See the list of flags.

CoeffReadCost 

This is a rough measure of how expensive it is to read one coefficient from this expression.

Definition at line 66 of file MatrixBase.h.

Constructor & Destructor Documentation

template<typename Derived>
MatrixBase< Derived >::MatrixBase (  )  [inline, protected]

Default constructor. Do nothing.

Definition at line 628 of file MatrixBase.h.

template<typename Derived>
MatrixBase< Derived >::MatrixBase ( int   )  [explicit, private]
template<typename Derived>
MatrixBase< Derived >::MatrixBase ( int  ,
int   
) [private]
template<typename Derived>
template<typename OtherDerived >
MatrixBase< Derived >::MatrixBase ( const MatrixBase< OtherDerived > &   )  [inline, explicit, private]

Member Function Documentation

template<typename Derived >
const MatrixBase< Derived >::AdjointReturnType MatrixBase< Derived >::adjoint (  )  const [inline]
Returns:
an expression of the adjoint (i.e. conjugate transpose) of *this.

Example: 

 Output: 


Warning:
If you want to replace a matrix by its own adjoint, do NOT do this: 
 m = m.adjoint(); // bug!!! caused by aliasing effect

 Instead, do: 
 m = m.adjoint().eval();



See also:
transpose(), conjugate(), class Transpose, class ei_scalar_conjugate_op 



Definition at line 177 of file Transpose.h.













template<typename Derived > 

      

        

          bool MatrixBase< Derived >::all 
          (
          void 
          
           ) 
           const [inline]
        

      






Returns:
true if all coefficients are true


CwiseAll  How to check whether a point is inside a box (using operator< and all())


Example: 


 Output: 


See also:
MatrixBase::any(), Cwise::operator<() 



Definition at line 92 of file BooleanRedux.h.













template<typename Derived > 

      

        

          bool MatrixBase< Derived >::any 
          (
          void 
          
           ) 
           const [inline]
        

      






Returns:
true if at least one coefficient is true


See also:
MatrixBase::all() 



Definition at line 116 of file BooleanRedux.h.













template<typename Derived > 

      

        

          const DiagonalMatrix< Derived > MatrixBase< Derived >::asDiagonal 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of a diagonal matrix with *this as vector of diagonal coefficients


AsDiagonalExample  How to build a diagonal matrix from a vector


Example: 


 Output: 


See also:
class DiagonalMatrix, isDiagonal() 



Definition at line 110 of file DiagonalMatrix.h.













template<typename Derived > 



template<typename CustomBinaryOp , typename OtherDerived > 

      

        

          EIGEN_STRONG_INLINE const CwiseBinaryOp< CustomBinaryOp, Derived, OtherDerived > MatrixBase< Derived >::binaryExpr 
          (
          const MatrixBase< OtherDerived > & 
           other, 
        

        

          
          
          const CustomBinaryOp & 
           func = CustomBinaryOp() 
        

        

          
          )
           const [inline]
        

      






Returns:
an expression of a custom coefficient-wise operator func of *this and other 


The template parameter CustomBinaryOp is the type of the functor of the custom operator (see class CwiseBinaryOp for an example)


CustomCwiseBinaryFunctors  How to use custom coeff wise binary functors


Here is an example illustrating the use of custom functors: 


 Output: 


See also:
class CwiseBinaryOp, MatrixBase::operator+, MatrixBase::operator-, Cwise::operator*, Cwise::operator/ 



Definition at line 299 of file CwiseBinaryOp.h.













template<typename Derived > 



template<int BlockRows, int BlockCols> 

      

        

          const BlockReturnType< Derived, BlockRows, BlockCols >::Type MatrixBase< Derived >::block 
          (
          int 
           startRow, 
        

        

          
          
          int 
           startCol 
        

        

          
          )
           const [inline]
        

      






This is the const version of block<>(int, int). 



Definition at line 701 of file Block.h.













template<typename Derived > 



template<int BlockRows, int BlockCols> 

      

        

          BlockReturnType< Derived, BlockRows, BlockCols >::Type MatrixBase< Derived >::block 
          (
          int 
           startRow, 
        

        

          
          
          int 
           startCol 
        

        

          
          )
           [inline]
        

      






Returns:
a fixed-size expression of a block in *this.


The template parameters BlockRows and BlockCols are the number of rows and columns in the block.


Parameters:

  

    
startRow the first row in the block 

    
startCol the first column in the block

  

  




BlockSubMatrixFixedSize  How to reference a sub-matrix (fixed-size)


Example: 


 Output: 


Note:
since block is a templated member, the keyword template has to be used if the matrix type is also a template parameter: 
 m.template block<3,3>(1,1); 



See also:
class Block, block(int,int,int,int) 



Definition at line 692 of file Block.h.













template<typename Derived > 

      

        

          const BlockReturnType< Derived >::Type MatrixBase< Derived >::block 
          (
          int 
           startRow, 
        

        

          
          
          int 
           startCol, 
        

        

          
          
          int 
           blockRows, 
        

        

          
          
          int 
           blockCols 
        

        

          
          )
           const [inline]
        

      






This is the const version of block(int,int,int,int). 



Definition at line 313 of file Block.h.













template<typename Derived > 

      

        

          BlockReturnType< Derived >::Type MatrixBase< Derived >::block 
          (
          int 
           startRow, 
        

        

          
          
          int 
           startCol, 
        

        

          
          
          int 
           blockRows, 
        

        

          
          
          int 
           blockCols 
        

        

          
          )
           [inline]
        

      






Returns:
a dynamic-size expression of a block in *this.


Parameters:

  

    
startRow the first row in the block 

    
startCol the first column in the block 

    
blockRows the number of rows in the block 

    
blockCols the number of columns in the block

  

  




BlockIntIntIntInt  How to reference a sub-matrix (dynamic-size)


Example: 


 Output: 


Note:
Even though the returned expression has dynamic size, in the case when it is applied to a fixed-size matrix, it inherits a fixed maximal size, which means that evaluating it does not cause a dynamic memory allocation.


See also:
class Block, block(int,int) 



Definition at line 305 of file Block.h.













template<typename Derived > 



template<typename NewType > 

      

        

          EIGEN_STRONG_INLINE const CwiseUnaryOp< ei_scalar_cast_op< typename ei_traits< Derived >::Scalar, NewType >, Derived > MatrixBase< Derived >::cast 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of *this with the Scalar type casted to NewScalar.


The template parameter NewScalar is the type we are casting the scalars to.


See also:
class CwiseUnaryOp 



Definition at line 192 of file CwiseUnaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const ei_traits< Derived >::Scalar MatrixBase< Derived >::coeff 
          (
          int 
           index
           ) 
           const [inline]
        

      






Short version: don't use this function, use operator[](int) const  instead.


Long version: this function is similar to operator[](int) const , but without the assertion. Use this for limiting the performance cost of debugging code when doing repeated coefficient access. Only use this when it is guaranteed that the parameter index is in range.


If EIGEN_INTERNAL_DEBUGGING is defined, an assertion will be made, making this function equivalent to operator[](int) const .


See also:
operator[](int) const, coeffRef(int), coeff(int,int) const 



Reimplemented in Select< ConditionMatrixType, ThenMatrixType, ElseMatrixType >, Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, CwiseBinaryOp< BinaryOp, Lhs, Rhs >, CwiseNullaryOp< NullaryOp, MatrixType >, CwiseUnaryOp< UnaryOp, MatrixType >, DiagonalCoeffs< MatrixType >, Flagged< ExpressionType, Added, Removed >, MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, NestByValue< ExpressionType >, Product< LhsNested, RhsNested, ProductMode >, Transpose< MatrixType >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 116 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const ei_traits< Derived >::Scalar MatrixBase< Derived >::coeff 
          (
          int 
           row, 
        

        

          
          
          int 
           col 
        

        

          
          )
           const [inline]
        

      






Short version: don't use this function, use operator()(int,int) const  instead.


Long version: this function is similar to operator()(int,int) const , but without the assertion. Use this for limiting the performance cost of debugging code when doing repeated coefficient access. Only use this when it is guaranteed that the parameters row and col are in range.


If EIGEN_INTERNAL_DEBUGGING is defined, an assertion will be made, making this function equivalent to operator()(int,int) const .


See also:
operator()(int,int) const, coeffRef(int,int), coeff(int) const 



Reimplemented in PartialReduxExpr< MatrixType, MemberOp, Direction >, Select< ConditionMatrixType, ThenMatrixType, ElseMatrixType >, Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, CwiseBinaryOp< BinaryOp, Lhs, Rhs >, CwiseNullaryOp< NullaryOp, MatrixType >, CwiseUnaryOp< UnaryOp, MatrixType >, DiagonalCoeffs< MatrixType >, DiagonalMatrix< CoeffsVectorType >, Product< LhsNested, RhsNested, DiagonalProduct >, Flagged< ExpressionType, Added, Removed >, MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, Minor< MatrixType >, NestByValue< ExpressionType >, Part< MatrixType, Mode >, Product< LhsNested, RhsNested, ProductMode >, Transpose< MatrixType >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 44 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE ei_traits< Derived >::Scalar & MatrixBase< Derived >::coeffRef 
          (
          int 
           index
           ) 
           [inline]
        

      






Short version: don't use this function, use operator[](int) instead.


Long version: this function is similar to operator[](int), but without the assertion. Use this for limiting the performance cost of debugging code when doing repeated coefficient access. Only use this when it is guaranteed that the parameters row and col are in range.


If EIGEN_INTERNAL_DEBUGGING is defined, an assertion will be made, making this function equivalent to operator[](int).


See also:
operator[](int), coeff(int) const, coeffRef(int,int) 



Reimplemented in Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, DiagonalCoeffs< MatrixType >, Flagged< ExpressionType, Added, Removed >, MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, NestByValue< ExpressionType >, SwapWrapper< ExpressionType >, Transpose< MatrixType >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 170 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE ei_traits< Derived >::Scalar & MatrixBase< Derived >::coeffRef 
          (
          int 
           row, 
        

        

          
          
          int 
           col 
        

        

          
          )
           [inline]
        

      






Short version: don't use this function, use operator()(int,int) instead.


Long version: this function is similar to operator()(int,int), but without the assertion. Use this for limiting the performance cost of debugging code when doing repeated coefficient access. Only use this when it is guaranteed that the parameters row and col are in range.


If EIGEN_INTERNAL_DEBUGGING is defined, an assertion will be made, making this function equivalent to operator()(int,int).


See also:
operator()(int,int), coeff(int, int) const, coeffRef(int) 



Reimplemented in Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, DiagonalCoeffs< MatrixType >, Flagged< ExpressionType, Added, Removed >, MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, Minor< MatrixType >, NestByValue< ExpressionType >, Part< MatrixType, Mode >, SwapWrapper< ExpressionType >, Transpose< MatrixType >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 80 of file Coeffs.h.













template<typename Derived > 

      

        

          const MatrixBase< Derived >::ColXpr MatrixBase< Derived >::col 
          (
          int 
           i
           ) 
           const [inline]
        

      






This is the const version of col(). 



Reimplemented in Part< MatrixType, Mode >.



Definition at line 724 of file Block.h.













template<typename Derived > 

      

        

          MatrixBase< Derived >::ColXpr MatrixBase< Derived >::col 
          (
          int 
           i
           ) 
           [inline]
        

      






Returns:
an expression of the i-th column of *this. Note that the numbering starts at 0.


BlockColumn  How to reference a single column of a matrix


Example: 


 Output: 


See also:
row(), class Block 



Reimplemented in Part< MatrixType, Mode >.



Definition at line 716 of file Block.h.













template<typename Derived> 

      

        

          int MatrixBase< Derived >::cols 
          (
          
           ) 
           const [inline]
        

      






Returns:
the number of columns. 


See also:
rows(), ColsAtCompileTime 



Reimplemented in PartialReduxExpr< MatrixType, MemberOp, Direction >, Select< ConditionMatrixType, ThenMatrixType, ElseMatrixType >, Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, CwiseBinaryOp< BinaryOp, Lhs, Rhs >, CwiseNullaryOp< NullaryOp, MatrixType >, CwiseUnaryOp< UnaryOp, MatrixType >, DiagonalCoeffs< MatrixType >, DiagonalMatrix< CoeffsVectorType >, Product< LhsNested, RhsNested, DiagonalProduct >, Flagged< ExpressionType, Added, Removed >, MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, Minor< MatrixType >, NestByValue< ExpressionType >, Part< MatrixType, Mode >, Product< LhsNested, RhsNested, ProductMode >, SwapWrapper< ExpressionType >, Transpose< MatrixType >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 156 of file MatrixBase.h.













template<typename Derived > 

      

        

          const PartialRedux< Derived, Vertical > MatrixBase< Derived >::colwise 
          (
          
           ) 
           const [inline]
        

      






Returns:
a PartialRedux wrapper of *this providing additional partial reduction operations


Example: 


 Output: 


See also:
rowwise(), class PartialRedux 



Definition at line 313 of file PartialRedux.h.













template<typename Derived> 



template<typename OtherDerived > 

      

        

          void MatrixBase< Derived >::computeInverse 
          (
          MatrixBase< OtherDerived > * 
           result
           ) 
           const [inline]
        

      






Computes the matrix inverse of this matrix.


Note:
This matrix must be invertible, otherwise the result is undefined.


Parameters:

  

    
result Pointer to the matrix in which to store the result.

  

  




Example: 


 Output: 


See also:
inverse() 



Definition at line 294 of file Inverse.h.













template<typename Derived> 



template<typename ResultType > 

      

        

          void MatrixBase< Derived >::computeInverse 
          (
          MatrixBase< ResultType > * 
           result
           ) 
           const [inline]
        

      

















template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE MatrixBase< Derived >::ConjugateReturnType MatrixBase< Derived >::conjugate 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of the complex conjugate of *this.


See also:
adjoint() 



Definition at line 163 of file CwiseUnaryOp.h.













template<typename Derived> 

      

        

          Derived& MatrixBase< Derived >::const_cast_derived 
          (
          
           ) 
           const [inline]
        

      







Definition at line 545 of file MatrixBase.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ConstantReturnType MatrixBase< Derived >::Constant 
          (
          const Scalar & 
           value
           ) 
           [inline, static]
        

      






Returns:
an expression of a constant matrix of value value 


This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.


The template parameter CustomNullaryOp is the type of the functor.


See also:
class CwiseNullaryOp 



Definition at line 225 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ConstantReturnType MatrixBase< Derived >::Constant 
          (
          int 
           size, 
        

        

          
          
          const Scalar & 
           value 
        

        

          
          )
           [inline, static]
        

      






Returns:
an expression of a constant matrix of value value 


The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.


The template parameter CustomNullaryOp is the type of the functor.


See also:
class CwiseNullaryOp 



Definition at line 209 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ConstantReturnType MatrixBase< Derived >::Constant 
          (
          int 
           rows, 
        

        

          
          
          int 
           cols, 
        

        

          
          
          const Scalar & 
           value 
        

        

          
          )
           [inline, static]
        

      






Returns:
an expression of a constant matrix of value value 


The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.


The template parameter CustomNullaryOp is the type of the functor.


See also:
class CwiseNullaryOp 



Definition at line 187 of file CwiseNullaryOp.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          EIGEN_STRONG_INLINE void MatrixBase< Derived >::copyCoeff 
          (
          int 
           index, 
        

        

          
          
          const MatrixBase< OtherDerived > & 
           other 
        

        

          
          )
           [inline]
        

      







Reimplemented in SwapWrapper< ExpressionType >.



Definition at line 343 of file Coeffs.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          EIGEN_STRONG_INLINE void MatrixBase< Derived >::copyCoeff 
          (
          int 
           row, 
        

        

          
          
          int 
           col, 
        

        

          
          
          const MatrixBase< OtherDerived > & 
           other 
        

        

          
          )
           [inline]
        

      







Reimplemented in SwapWrapper< ExpressionType >.



Definition at line 327 of file Coeffs.h.













template<typename Derived > 



template<typename OtherDerived , int StoreMode, int LoadMode> 

      

        

          EIGEN_STRONG_INLINE void MatrixBase< Derived >::copyPacket 
          (
          int 
           index, 
        

        

          
          
          const MatrixBase< OtherDerived > & 
           other 
        

        

          
          )
           [inline]
        

      







Reimplemented in SwapWrapper< ExpressionType >.



Definition at line 375 of file Coeffs.h.













template<typename Derived > 



template<typename OtherDerived , int StoreMode, int LoadMode> 

      

        

          EIGEN_STRONG_INLINE void MatrixBase< Derived >::copyPacket 
          (
          int 
           row, 
        

        

          
          
          int 
           col, 
        

        

          
          
          const MatrixBase< OtherDerived > & 
           other 
        

        

          
          )
           [inline]
        

      







Reimplemented in SwapWrapper< ExpressionType >.



Definition at line 358 of file Coeffs.h.













template<typename Derived > 



template<int CRows, int CCols> 

      

        

          const BlockReturnType< Derived, CRows, CCols >::Type MatrixBase< Derived >::corner 
          (
          CornerType 
           type
           ) 
           const [inline]
        

      






This is the const version of corner<int, int>(CornerType). 



Definition at line 654 of file Block.h.













template<typename Derived > 



template<int CRows, int CCols> 

      

        

          BlockReturnType< Derived, CRows, CCols >::Type MatrixBase< Derived >::corner 
          (
          CornerType 
           type
           ) 
           [inline]
        

      






Returns:
a fixed-size expression of a corner of *this.


Parameters:

  

    
type the type of corner. Can be Eigen::TopLeft, Eigen::TopRight, Eigen::BottomLeft, Eigen::BottomRight.

  

  




The template parameters CRows and CCols arethe number of rows and columns in the corner.


Example: 


 Output: 


See also:
class Block, block(int,int,int,int) 



Definition at line 633 of file Block.h.













template<typename Derived > 

      

        

          const BlockReturnType< Derived >::Type MatrixBase< Derived >::corner 
          (
          CornerType 
           type, 
        

        

          
          
          int 
           cRows, 
        

        

          
          
          int 
           cCols 
        

        

          
          )
           const [inline]
        

      






This is the const version of corner(CornerType, int, int). 



Definition at line 601 of file Block.h.













template<typename Derived > 

      

        

          BlockReturnType< Derived >::Type MatrixBase< Derived >::corner 
          (
          CornerType 
           type, 
        

        

          
          
          int 
           cRows, 
        

        

          
          
          int 
           cCols 
        

        

          
          )
           [inline]
        

      






Returns:
a dynamic-size expression of a corner of *this.


Parameters:

  

    
type the type of corner. Can be Eigen::TopLeft, Eigen::TopRight, Eigen::BottomLeft, Eigen::BottomRight. 

    
cRows the number of rows in the corner 

    
cCols the number of columns in the corner

  

  




BlockCornerDynamicSize  How to reference a sub-corner of a matrix


Example: 


 Output: 


Note:
Even though the returned expression has dynamic size, in the case when it is applied to a fixed-size matrix, it inherits a fixed maximal size, which means that evaluating it does not cause a dynamic memory allocation.


See also:
class Block, block(int,int,int,int) 



Definition at line 581 of file Block.h.













template<typename Derived > 

      

        

          int MatrixBase< Derived >::count 
          (
          
           ) 
           const [inline]
        

      






Returns:
the number of coefficients which evaluate to true


See also:
MatrixBase::all(), MatrixBase::any() 



Definition at line 140 of file BooleanRedux.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          MatrixBase< Derived >::PlainMatrixType MatrixBase< Derived >::cross 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           const [inline]
        

      






Returns:
the cross product of *this and other 


Here is a very good explanation of cross-product: http://xkcd.com/199/ 



Definition at line 38 of file OrthoMethods.h.













template<typename Derived > 

      

        

          Cwise< Derived > MatrixBase< Derived >::cwise 
          (
          
           ) 
           [inline]
        

      






Returns:
a Cwise wrapper of *this providing additional coefficient-wise operations


Example: 


 Output: 


See also:
class Cwise, cwise() const 



Definition at line 209 of file Cwise.h.













template<typename Derived > 

      

        

          const Cwise< Derived > MatrixBase< Derived >::cwise 
          (
          
           ) 
           const [inline]
        

      






Returns:
a Cwise wrapper of *this providing additional coefficient-wise operations


Example: 


 Output: 


See also:
class Cwise, cwise() 



Definition at line 195 of file Cwise.h.













template<typename Derived> 

      

        

          Derived& MatrixBase< Derived >::derived 
          (
          
           ) 
           [inline]
        

      







Definition at line 544 of file MatrixBase.h.













template<typename Derived> 

      

        

          const Derived& MatrixBase< Derived >::derived 
          (
          
           ) 
           const [inline]
        

      







Definition at line 543 of file MatrixBase.h.













template<typename Derived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::determinant 
          (
          
           ) 
           const [inline]
        

      






Returns:
the determinant of this matrix 



Definition at line 116 of file Determinant.h.













template<typename Derived > 

      

        

          const DiagonalCoeffs< Derived > MatrixBase< Derived >::diagonal 
          (
          
           ) 
           const [inline]
        

      






This is the const version of diagonal(). 



Reimplemented in DiagonalMatrix< CoeffsVectorType >.



Definition at line 119 of file DiagonalCoeffs.h.













template<typename Derived > 

      

        

          DiagonalCoeffs< Derived > MatrixBase< Derived >::diagonal 
          (
          
           ) 
           [inline]
        

      






Returns:
an expression of the main diagonal of the matrix *this 


*this is not required to be square.


Example: 


 Output: 


See also:
class DiagonalCoeffs 



Definition at line 111 of file DiagonalCoeffs.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::dot 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           const [inline]
        

      






Returns:
the dot product of *this with other.


Note:
If the scalar type is complex numbers, then this function returns the hermitian (sesquilinear) dot product, linear in the first variable and conjugate-linear in the second variable.


See also:
squaredNorm(), norm() 



Definition at line 259 of file Dot.h.













template<typename Derived > 

      

        

          Matrix< typename NumTraits< typename ei_traits< Derived >::Scalar >::Real, ei_traits< Derived >::ColsAtCompileTime, 1 > MatrixBase< Derived >::eigenvalues 
          (
          
           ) 
           const [inline]
        

      






Returns:
a vector listing the eigenvalues of this matrix. 



Definition at line 294 of file SelfAdjointEigenSolver.h.













template<typename Derived > 



template<int Size> 

      

        

          const BlockReturnType< Derived, Size >::SubVectorType MatrixBase< Derived >::end 
          (
          
           ) 
           const [inline]
        

      






This is the const version of end<int>. 



Definition at line 551 of file Block.h.













template<typename Derived > 



template<int Size> 

      

        

          BlockReturnType< Derived, Size >::SubVectorType MatrixBase< Derived >::end 
          (
          
           ) 
           [inline]
        

      






Returns:
a fixed-size expression of the last coefficients of *this.


The template parameter Size is the number of coefficients in the block


Example: 


 Output: 


See also:
class Block 



Definition at line 537 of file Block.h.













template<typename Derived > 

      

        

          const BlockReturnType< Derived, Dynamic >::SubVectorType MatrixBase< Derived >::end 
          (
          int 
           size
           ) 
           const [inline]
        

      






This is the const version of end(int). 



Definition at line 438 of file Block.h.













template<typename Derived > 

      

        

          BlockReturnType< Derived, Dynamic >::SubVectorType MatrixBase< Derived >::end 
          (
          int 
           size
           ) 
           [inline]
        

      






Returns:
a dynamic-size expression of the last coefficients of *this.


Parameters:

  

    
size the number of coefficients in the block

  

  




BlockEnd  How to reference the end of a vector (fixed-size)


Example: 


 Output: 


Note:
Even though the returned expression has dynamic size, in the case when it is applied to a fixed-size vector, it inherits a fixed maximal size, which means that evaluating it does not cause a dynamic memory allocation.


See also:
class Block, block(int,int) 



Definition at line 422 of file Block.h.













template<typename Derived> 

      

        

          EIGEN_STRONG_INLINE const ei_eval<Derived>::type MatrixBase< Derived >::eval 
          (
          
           ) 
           const [inline]
        

      






Returns:
the matrix or vector obtained by evaluating this expression.


Notice that in the case of a plain matrix or vector (not an expression) this function just returns a const reference, in order to avoid a useless copy. 



Definition at line 491 of file MatrixBase.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE void MatrixBase< Derived >::fill 
          (
          const Scalar & 
           value
           ) 
           [inline]
        

      






Alias for setConstant(): sets all coefficients in this expression to value.


See also:
setConstant(), Constant(), class CwiseNullaryOp 



Definition at line 258 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          const WithFormat< Derived > MatrixBase< Derived >::format 
          (
          const IOFormat & 
           fmt
           ) 
           const [inline]
        

      






Returns:
a WithFormat proxy object allowing to print a matrix the with given format fmt.


See class IOFormat for some examples.


See also:
class IOFormat, class WithFormat 



Definition at line 117 of file IO.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::IdentityReturnType MatrixBase< Derived >::Identity 
          (
          int 
           rows, 
        

        

          
          
          int 
           cols 
        

        

          
          )
           [inline, static]
        

      






Returns:
an expression of the identity matrix (not necessarily square).


The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Identity() should be used instead.


Identity  How to get an identity matrix


Example: 


 Output: 


See also:
Identity(), setIdentity(), isIdentity() 



Definition at line 588 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::IdentityReturnType MatrixBase< Derived >::Identity 
          (
          
           ) 
           [inline, static]
        

      






Returns:
an expression of the identity matrix (not necessarily square).


This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variant taking size arguments.


Example: 


 Output: 


See also:
Identity(int,int), setIdentity(), isIdentity() 



Definition at line 605 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ImagReturnType MatrixBase< Derived >::imag 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of the imaginary part of *this.


See also:
real() 



Definition at line 180 of file CwiseUnaryOp.h.













template<typename Derived> 

      

        

          int MatrixBase< Derived >::innerSize 
          (
          
           ) 
           const [inline]
        

      






Returns:
the size of the inner dimension according to the storage order, i.e., the number of rows for a columns major matrix, and the number of cols otherwise 



Definition at line 173 of file MatrixBase.h.













template<typename Derived > 

      

        

          const MatrixBase< Derived >::PlainMatrixType MatrixBase< Derived >::inverse 
          (
          
           ) 
           const [inline]
        

      






Returns:
the matrix inverse of this matrix.


Note:
This matrix must be invertible, otherwise the result is undefined.



This method returns a matrix by value, which can be inefficient. To avoid that overhead, use computeInverse() instead.


Example: 


 Output: 


See also:
computeInverse() 



Definition at line 316 of file Inverse.h.













template<typename Derived> 



template<typename OtherDerived > 

      

        

          bool MatrixBase< Derived >::isApprox 
          (
          const MatrixBase< OtherDerived > & 
           other, 
        

        

          
          
          typename NumTraits< Scalar >::Real 
           prec 
        

        

          
          )
           const [inline]
        

      






Returns:
true if *this is approximately equal to other, within the precision determined by prec.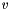


Note:
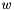The fuzzy compares are done multiplicatively. Two vectors $ v $ and $ w $ are considered to be approximately equal within precision 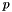$ p $ if 

\[ \Vert v - w \Vert \leqslant p\,\min(\Vert v\Vert, \Vert w\Vert). \]


 For matrices, the comparison is done using the Hilbert-Schmidt norm (aka Frobenius norm L2 norm).



Because of the multiplicativeness of this comparison, one can't use this function to check whether *this is approximately equal to the zero matrix or vector. Indeed, isApprox(zero) returns false unless *this itself is exactly the zero matrix or vector. If you want to test whether *this is zero, use ei_isMuchSmallerThan(const RealScalar&, RealScalar) instead.


See also:
ei_isMuchSmallerThan(const RealScalar&, RealScalar) const 



Definition at line 50 of file Fuzzy.h.













template<typename Derived> 



template<typename OtherDerived > 

      

        

          bool MatrixBase< Derived >::isApprox 
          (
          const MatrixBase< OtherDerived > & 
           other, 
        

        

          
          
          RealScalar 
           prec = precision< Scalar >() 
        

        

          
          )
           const [inline]
        

      

















template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isApproxToConstant 
          (
          const Scalar & 
           value, 
        

        

          
          
          RealScalar 
           prec = precision<Scalar>() 
        

        

          
          )
           const [inline]
        

      






Returns:
true if all coefficients in this matrix are approximately equal to value, to within precision prec 



Definition at line 234 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isConstant 
          (
          const Scalar & 
           value, 
        

        

          
          
          RealScalar 
           prec = precision<Scalar>() 
        

        

          
          )
           const [inline]
        

      






This is just an alias for isApproxToConstant().


Returns:
true if all coefficients in this matrix are approximately equal to value, to within precision prec 



Definition at line 248 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isDiagonal 
          (
          RealScalar 
           prec = precision<Scalar>()
           ) 
           const [inline]
        

      






Returns:
true if *this is approximately equal to a diagonal matrix, within the precision given by prec.


Example: 


 Output: 


See also:
asDiagonal() 



Definition at line 126 of file DiagonalMatrix.h.













template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isIdentity 
          (
          RealScalar 
           prec = precision<Scalar>()
           ) 
           const [inline]
        

      






Returns:
true if *this is approximately equal to the identity matrix (not necessarily square), within the precision given by prec.


Example: 


 Output: 


See also:
class CwiseNullaryOp, Identity(), Identity(int,int), setIdentity() 



Definition at line 622 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isLowerTriangular 
          (
          RealScalar 
           prec = precision<Scalar>()
           ) 
           const [inline]
        

      






Returns:
true if *this is approximately equal to a lower triangular matrix, within the precision given by prec.


See also:
isUpperTriangular(), extract(), part(), marked() 



Definition at line 333 of file Part.h.













template<typename Derived> 



template<typename OtherDerived > 

      

        

          bool MatrixBase< Derived >::isMuchSmallerThan 
          (
          const MatrixBase< OtherDerived > & 
           other, 
        

        

          
          
          typename NumTraits< Scalar >::Real 
           prec 
        

        

          
          )
           const [inline]
        

      






Returns:
true if the norm of *this is much smaller than the norm of other, within the precision determined by prec.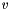


Note:
The fuzzy compares are done multiplicatively. A vector $ v $ is considered to be much smaller than a vector 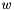$ w $ within precision 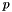$ p $ if 

\[ \Vert v \Vert \leqslant p\,\Vert w\Vert. \]


 For matrices, the comparison is done using the Hilbert-Schmidt norm.


See also:
isApprox(), isMuchSmallerThan(const RealScalar&, RealScalar) const 



Definition at line 94 of file Fuzzy.h.













template<typename Derived> 



template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isMuchSmallerThan 
          (
          const typename NumTraits< Scalar >::Real & 
           other, 
        

        

          
          
          typename NumTraits< Scalar >::Real 
           prec 
        

        

          
          )
           const [inline]
        

      






Returns:
true if the norm of *this is much smaller than other, within the precision determined by prec.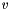


Note:
The fuzzy compares are done multiplicatively. A vector $ v $ is considered to be much smaller than 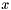$ x $ within precision 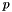$ p $ if 

\[ \Vert v \Vert \leqslant p\,\vert x\vert. \]





For matrices, the comparison is done using the Hilbert-Schmidt norm. For this reason, the value of the reference scalar other should come from the Hilbert-Schmidt norm of a reference matrix of same dimensions.


See also:
isApprox(), isMuchSmallerThan(const MatrixBase<OtherDerived>&, RealScalar) const 



Definition at line 74 of file Fuzzy.h.













template<typename Derived> 



template<typename OtherDerived > 

      

        

          bool MatrixBase< Derived >::isMuchSmallerThan 
          (
          const MatrixBase< OtherDerived > & 
           other, 
        

        

          
          
          RealScalar 
           prec = precision< Scalar >() 
        

        

          
          )
           const [inline]
        

      

















template<typename Derived> 

      

        

          bool MatrixBase< Derived >::isMuchSmallerThan 
          (
          const RealScalar & 
           other, 
        

        

          
          
          RealScalar 
           prec = precision< Scalar >() 
        

        

          
          )
           const
        

      

















template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isOnes 
          (
          RealScalar 
           prec = precision<Scalar>()
           ) 
           const [inline]
        

      






Returns:
true if *this is approximately equal to the matrix where all coefficients are equal to 1, within the precision given by prec.


Example: 


 Output: 


See also:
class CwiseNullaryOp, Ones() 



Definition at line 515 of file CwiseNullaryOp.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          bool MatrixBase< Derived >::isOrthogonal 
          (
          const MatrixBase< OtherDerived > & 
           other, 
        

        

          
          
          RealScalar 
           prec = precision<Scalar>() 
        

        

          
          )
           const [inline]
        

      






Returns:
true if *this is approximately orthogonal to other, within the precision given by prec.


Example: 


 Output: 


 

Definition at line 329 of file Dot.h.













template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isUnitary 
          (
          RealScalar 
           prec = precision<Scalar>()
           ) 
           const [inline]
        

      






Returns:
true if *this is approximately an unitary matrix, within the precision given by prec. In the case where the Scalar type is real numbers, a unitary matrix is an orthogonal matrix, whence the name.


Note:
This can be used to check whether a family of vectors forms an orthonormal basis. Indeed, m.isUnitary() returns true if and only if the columns (equivalently, the rows) of m form an orthonormal basis.


Example: 


 Output: 


 

Definition at line 348 of file Dot.h.













template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isUpperTriangular 
          (
          RealScalar 
           prec = precision<Scalar>()
           ) 
           const [inline]
        

      






Returns:
true if *this is approximately equal to an upper triangular matrix, within the precision given by prec.


See also:
isLowerTriangular(), extract(), part(), marked() 



Definition at line 311 of file Part.h.













template<typename Derived> 

      

        

          bool MatrixBase< Derived >::isVector 
          (
          
           ) 
           const [inline]
        

      






Returns:
true if either the number of rows or the number of columns is equal to 1. In other words, this function returns 
 rows()==1 || cols()==1 

 


See also:
rows(), cols(), IsVectorAtCompileTime. 



Definition at line 167 of file MatrixBase.h.













template<typename Derived > 

      

        

          bool MatrixBase< Derived >::isZero 
          (
          RealScalar 
           prec = precision<Scalar>()
           ) 
           const [inline]
        

      






Returns:
true if *this is approximately equal to the zero matrix, within the precision given by prec.


Example: 


 Output: 


See also:
class CwiseNullaryOp, Zero() 



Definition at line 383 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          const Flagged< Derived, 0, EvalBeforeNestingBit|EvalBeforeAssigningBit > MatrixBase< Derived >::lazy 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of *this with the following flags removed: EvalBeforeNestingBit and EvalBeforeAssigningBit.


Example: 


 Output: 


See also:
class Flagged, marked() 



Definition at line 144 of file Flagged.h.













template<typename Derived> 



template<typename Lhs , typename Rhs > 

      

        

          Derived& MatrixBase< Derived >::lazyAssign 
          (
          const SparseProduct< Lhs, Rhs, DenseTimeSparseProduct > & 
           product
           ) 
           [inline]
        

      







Definition at line 385 of file SparseProduct.h.













template<typename Derived> 



template<typename Lhs , typename Rhs > 

      

        

          Derived& MatrixBase< Derived >::lazyAssign 
          (
          const SparseProduct< Lhs, Rhs, SparseTimeDenseProduct > & 
           product
           ) 
           [inline]
        

      







Definition at line 337 of file SparseProduct.h.













template<typename Derived> 



template<typename Derived1 , typename Derived2 > 

      

        

          Derived& MatrixBase< Derived >::lazyAssign 
          (
          const SparseProduct< Derived1, Derived2, DenseTimeSparseProduct > & 
           product
           ) 
           [inline]
        

      

















template<typename Derived> 



template<typename Derived1 , typename Derived2 > 

      

        

          Derived& MatrixBase< Derived >::lazyAssign 
          (
          const SparseProduct< Derived1, Derived2, SparseTimeDenseProduct > & 
           product
           ) 
           [inline]
        

      

















template<typename Derived> 



template<typename OtherDerived > 

      

        

          Derived& MatrixBase< Derived >::lazyAssign 
          (
          const Flagged< OtherDerived, 0, EvalBeforeNestingBit|EvalBeforeAssigningBit > & 
           other
           ) 
           [inline]
        

      






Overloaded for cache friendly product evaluation 



Definition at line 245 of file MatrixBase.h.













template<typename Derived > 



template<typename Lhs , typename Rhs > 

      

        

          Derived & MatrixBase< Derived >::lazyAssign 
          (
          const Product< Lhs, Rhs, CacheFriendlyProduct > & 
           product
           ) 
           [inline]
        

      






Overloaded for cache friendly product evaluation 



Definition at line 756 of file Product.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::lazyAssign 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           [inline]
        

      






Copies other into *this without evaluating other. 


Returns:
a reference to *this. 



Definition at line 423 of file Assign.h.













template<typename Derived > 

      

        

          const LDLT< typename MatrixBase< Derived >::PlainMatrixType > MatrixBase< Derived >::ldlt 
          (
          
           ) 
           const [inline]
        

      






Returns:
the Cholesky decomposition without square root of *this 



Definition at line 187 of file LDLT.h.













template<typename Derived > 

      

        

          const LLT< typename MatrixBase< Derived >::PlainMatrixType > MatrixBase< Derived >::llt 
          (
          
           ) 
           const [inline]
        

      






Returns:
the LLT decomposition of *this 



Definition at line 215 of file LLT.h.













template<typename Derived > 



template<int p> 

      

        

          NumTraits< typename ei_traits< Derived >::Scalar >::Real MatrixBase< Derived >::lpNorm 
          (
          
           ) 
           const [inline]
        

      






Returns:
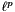the $ \ell^p $ norm of *this, that is, returns the p-th root of the sum of the p-th powers of the absolute values of the coefficients of *this. If p is the special value Eigen::Infinity, this function returns the 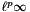$ \ell^p\infty $ norm, that is the maximum of the absolute values of the coefficients of *this.


See also:
norm() 



Definition at line 75 of file Norms.h.













template<typename Derived > 

      

        

          const LU< typename MatrixBase< Derived >::PlainMatrixType > MatrixBase< Derived >::lu 
          (
          
           ) 
           const [inline]
        

      






Returns:
the LU decomposition of *this.


See also:
class LU 



Definition at line 538 of file LU.h.













template<typename Derived > 



template<unsigned int Added> 

      

        

          const Flagged< Derived, Added, 0 > MatrixBase< Derived >::marked 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of *this with added flags


MarkExample  How to mark a triangular matrix as triangular


Example: 


 Output: 


See also:
class Flagged, extract(), part() 



Definition at line 129 of file Flagged.h.













template<typename Derived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::maxCoeff 
          (
          int * 
           index
           ) 
           const [inline]
        

      






Returns:
the maximum of all coefficients of *this and puts in *index its location.


See also:
MatrixBase::maxCoeff(int*,int*), MatrixBase::minCoeff(int*,int*), MatrixBase::visitor(), MatrixBase::maxCoeff() 



Definition at line 219 of file Visitor.h.













template<typename Derived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::maxCoeff 
          (
          int * 
           row, 
        

        

          
          
          int * 
           col 
        

        

          
          )
           const [inline]
        

      






Returns:
the maximum of all coefficients of *this and puts in *row and *col its location.


See also:
MatrixBase::minCoeff(int*,int*), MatrixBase::visitor(), MatrixBase::maxCoeff() 



Definition at line 203 of file Visitor.h.













template<typename Derived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::maxCoeff 
          (
          
           ) 
           const [inline]
        

      






Returns:
the maximum of all coefficients of *this 



Definition at line 112 of file Redux.h.













template<typename Derived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::minCoeff 
          (
          int * 
           index
           ) 
           const [inline]
        

      






Returns:
the minimum of all coefficients of *this and puts in *index its location.


See also:
MatrixBase::minCoeff(int*,int*), MatrixBase::maxCoeff(int*,int*), MatrixBase::visitor(), MatrixBase::minCoeff() 



Definition at line 187 of file Visitor.h.













template<typename Derived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::minCoeff 
          (
          int * 
           row, 
        

        

          
          
          int * 
           col 
        

        

          
          )
           const [inline]
        

      






Returns:
the minimum of all coefficients of *this and puts in *row and *col its location.


See also:
MatrixBase::minCoeff(int*), MatrixBase::maxCoeff(int*,int*), MatrixBase::visitor(), MatrixBase::minCoeff() 



Definition at line 171 of file Visitor.h.













template<typename Derived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::minCoeff 
          (
          
           ) 
           const [inline]
        

      






Returns:
the minimum of all coefficients of *this 



Definition at line 103 of file Redux.h.













template<typename Derived > 

      

        

          const Minor< Derived > MatrixBase< Derived >::minor 
          (
          int 
           row, 
        

        

          
          
          int 
           col 
        

        

          
          )
           const [inline]
        

      






This is the const version of minor(). 



Definition at line 117 of file Minor.h.













template<typename Derived > 

      

        

          Minor< Derived > MatrixBase< Derived >::minor 
          (
          int 
           row, 
        

        

          
          
          int 
           col 
        

        

          
          )
           [inline]
        

      






Returns:
an expression of the (row, col)-minor of *this, i.e. an expression constructed from *this by removing the specified row and column.


Example: 


 Output: 


See also:
class Minor 



Definition at line 108 of file Minor.h.













template<typename Derived > 

      

        

          const NestByValue< Derived > MatrixBase< Derived >::nestByValue 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of the temporary version of *this. 



Definition at line 112 of file NestByValue.h.













template<typename Derived> 

      

        

          int MatrixBase< Derived >::nonZeros 
          (
          
           ) 
           const [inline]
        

      






Returns:
the number of nonzero coefficients which is in practice the number of stored coefficients. 



Definition at line 162 of file MatrixBase.h.













template<typename Derived > 

      

        

          NumTraits< typename ei_traits< Derived >::Scalar >::Real MatrixBase< Derived >::norm 
          (
          
           ) 
           const [inline]
        

      






Returns:
the l2 norm of *this, i.e., for vectors, the square root of the dot product of *this with itself.


See also:
dot(), squaredNorm() 



Definition at line 287 of file Dot.h.













template<typename Derived > 

      

        

          void MatrixBase< Derived >::normalize 
          (
          
           ) 
           [inline]
        

      






Normalizes the vector, i.e. divides it by its own norm.


See also:
norm(), normalized() 



Definition at line 315 of file Dot.h.













template<typename Derived > 

      

        

          const MatrixBase< Derived >::PlainMatrixType MatrixBase< Derived >::normalized 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of the quotient of *this by its own norm.


See also:
norm(), normalize() 



Definition at line 300 of file Dot.h.













template<typename Derived > 



template<typename CustomNullaryOp > 

      

        

          EIGEN_STRONG_INLINE const CwiseNullaryOp< CustomNullaryOp, Derived > MatrixBase< Derived >::NullaryExpr 
          (
          const CustomNullaryOp & 
           func
           ) 
           [inline, static]
        

      






Returns:
an expression of a matrix defined by a custom functor func 


This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.


The template parameter CustomNullaryOp is the type of the functor.


See also:
class CwiseNullaryOp 



Definition at line 167 of file CwiseNullaryOp.h.













template<typename Derived > 



template<typename CustomNullaryOp > 

      

        

          EIGEN_STRONG_INLINE const CwiseNullaryOp< CustomNullaryOp, Derived > MatrixBase< Derived >::NullaryExpr 
          (
          int 
           size, 
        

        

          
          
          const CustomNullaryOp & 
           func 
        

        

          
          )
           [inline, static]
        

      






Returns:
an expression of a matrix defined by a custom functor func 


The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.


The template parameter CustomNullaryOp is the type of the functor.


See also:
class CwiseNullaryOp 



Definition at line 147 of file CwiseNullaryOp.h.













template<typename Derived > 



template<typename CustomNullaryOp > 

      

        

          EIGEN_STRONG_INLINE const CwiseNullaryOp< CustomNullaryOp, Derived > MatrixBase< Derived >::NullaryExpr 
          (
          int 
           rows, 
        

        

          
          
          int 
           cols, 
        

        

          
          
          const CustomNullaryOp & 
           func 
        

        

          
          )
           [inline, static]
        

      






Returns:
an expression of a matrix defined by a custom functor func 


The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.


The template parameter CustomNullaryOp is the type of the functor.


See also:
class CwiseNullaryOp 



Definition at line 124 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ConstantReturnType MatrixBase< Derived >::Ones 
          (
          
           ) 
           [inline, static]
        

      






Returns:
an expression of a fixed-size matrix or vector where all coefficients equal one.


This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.


Example: 


 Output: 


See also:
Ones(int), Ones(int,int), isOnes(), class Ones 



Definition at line 500 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ConstantReturnType MatrixBase< Derived >::Ones 
          (
          int 
           size
           ) 
           [inline, static]
        

      






Returns:
an expression of a vector where all coefficients equal one.


The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Ones() should be used instead.


Example: 


 Output: 


See also:
Ones(), Ones(int,int), isOnes(), class Ones 



Definition at line 483 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ConstantReturnType MatrixBase< Derived >::Ones 
          (
          int 
           rows, 
        

        

          
          
          int 
           cols 
        

        

          
          )
           [inline, static]
        

      






Returns:
an expression of a matrix where all coefficients equal one.


The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Ones() should be used instead.


One  How to get a matrix with all coefficients equal one


Example: 


 Output: 


See also:
Ones(), Ones(int), isOnes(), class Ones 



Definition at line 460 of file CwiseNullaryOp.h.













template<typename Derived> 



template<typename OtherDerived > 

      

        

          bool MatrixBase< Derived >::operator!= 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           const [inline]
        

      







Definition at line 479 of file MatrixBase.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE ei_traits< Derived >::Scalar & MatrixBase< Derived >::operator() 
          (
          int 
           index
           ) 
           [inline]
        

      






Returns:
a reference to the coefficient at given index.


This is synonymous to operator[](int).


This method is allowed only for vector expressions, and for matrix expressions having the LinearAccessBit.


See also:
operator[](int) const, operator()(int,int), x(), y(), z(), w() 



Definition at line 200 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const ei_traits< Derived >::Scalar MatrixBase< Derived >::operator() 
          (
          int 
           index
           ) 
           const [inline]
        

      






Returns:
the coefficient at given index.


This is synonymous to operator[](int) const.


This method is allowed only for vector expressions, and for matrix expressions having the LinearAccessBit.


See also:
operator[](int), operator()(int,int) const, x() const, y() const, z() const, w() const 



Definition at line 148 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE ei_traits< Derived >::Scalar & MatrixBase< Derived >::operator() 
          (
          int 
           row, 
        

        

          
          
          int 
           col 
        

        

          
          )
           [inline]
        

      






Returns:
a reference to the coefficient at given the given row and column.


See also:
operator()(int,int) const, operator[](int) 



Definition at line 93 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const ei_traits< Derived >::Scalar MatrixBase< Derived >::operator() 
          (
          int 
           row, 
        

        

          
          
          int 
           col 
        

        

          
          )
           const [inline]
        

      






Returns:
the coefficient at given the given row and column.


See also:
operator()(int,int), operator[](int) const 



Definition at line 57 of file Coeffs.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          const ProductReturnType< Derived, OtherDerived >::Type MatrixBase< Derived >::operator* 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           const [inline]
        

      






Returns:
the matrix product of *this and other.


Note:
If instead of the matrix product you want the coefficient-wise product, see Cwise::operator*().


See also:
lazy(), operator*=(const MatrixBase&), Cwise::operator*() 



Definition at line 281 of file Product.h.













template<typename Derived> 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ScalarMultipleReturnType operator* 
          (
          const Scalar & 
           scalar
           ) 
           const [inline]
        

      







Definition at line 200 of file CwiseUnaryOp.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          Derived & MatrixBase< Derived >::operator*= 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           [inline]
        

      






replaces *this by *this * other.


Returns:
a reference to *this 



Definition at line 308 of file Product.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator*= 
          (
          const Scalar & 
           other
           ) 
           [inline]
        

      







Reimplemented in MapBase< Derived >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, and MapBase< Map< MatrixType, PacketAccess > >.



Definition at line 217 of file CwiseUnaryOp.h.













template<typename Derived> 



template<typename OtherDerived > 

      

        

          EIGEN_STRONG_INLINE const CwiseBinaryOp< ei_scalar_sum_op< typename ei_traits< Derived >::Scalar >, Derived, OtherDerived > operator+ 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           const [inline]
        

      






Returns:
an expression of the sum of *this and other 


Note:
If you want to add a given scalar to all coefficients, see Cwise::operator+().


See also:
class CwiseBinaryOp, MatrixBase::operator+=(), Cwise::operator+() 



Definition at line 178 of file CwiseBinaryOp.h.













template<typename Derived > 



template<typename Lhs , typename Rhs > 

      

        

          Derived & MatrixBase< Derived >::operator+= 
          (
          const Flagged< Product< Lhs, Rhs, CacheFriendlyProduct >, 0, EvalBeforeNestingBit|EvalBeforeAssigningBit > & 
           other
           ) 
           [inline]
        

      







Definition at line 735 of file Product.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator+= 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           [inline]
        

      






replaces *this by *this + other.


Returns:
a reference to *this 



Reimplemented in MapBase< Derived >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, and MapBase< Map< MatrixType, PacketAccess > >.



Definition at line 190 of file CwiseBinaryOp.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          EIGEN_STRONG_INLINE const CwiseBinaryOp< ei_scalar_difference_op< typename ei_traits< Derived >::Scalar >, Derived, OtherDerived > MatrixBase< Derived >::operator- 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           const [inline]
        

      






Returns:
an expression of the difference of *this and other 


Note:
If you want to substract a given scalar from all coefficients, see Cwise::operator-().


See also:
class CwiseBinaryOp, MatrixBase::operator-=(), Cwise::operator-() 



Definition at line 149 of file CwiseBinaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const CwiseUnaryOp< ei_scalar_opposite_op< typename ei_traits< Derived >::Scalar >, Derived > MatrixBase< Derived >::operator- 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of the opposite of *this 



Definition at line 125 of file CwiseUnaryOp.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator-= 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           [inline]
        

      






replaces *this by *this - other.


Returns:
a reference to *this 



Reimplemented in MapBase< Derived >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, and MapBase< Map< MatrixType, PacketAccess > >.



Definition at line 162 of file CwiseBinaryOp.h.













template<typename Derived> 

      

        

          EIGEN_STRONG_INLINE const CwiseUnaryOp< ei_scalar_quotient1_op< typename ei_traits< Derived >::Scalar >, Derived > operator/ 
          (
          const Scalar & 
           scalar
           ) 
           const [inline]
        

      







Definition at line 209 of file CwiseUnaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator/= 
          (
          const Scalar & 
           other
           ) 
           [inline]
        

      







Reimplemented in MapBase< Derived >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, and MapBase< Map< MatrixType, PacketAccess > >.



Definition at line 224 of file CwiseUnaryOp.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          CommaInitializer< Derived > MatrixBase< Derived >::operator<< 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           [inline]
        

      






See also:
operator<<(const Scalar&) 



Definition at line 147 of file CommaInitializer.h.













template<typename Derived > 

      

        

          CommaInitializer< Derived > MatrixBase< Derived >::operator<< 
          (
          const Scalar & 
           s
           ) 
           [inline]
        

      






 Convenient operator to set the coefficients of a matrix.


The coefficients must be provided in a row major order and exactly match the size of the matrix. Otherwise an assertion is raised.


CommaInit  How to easily set all the coefficients of a matrix


Example: 


 Output: 


See also:
CommaInitializer::finished(), class CommaInitializer 



Definition at line 138 of file CommaInitializer.h.













template<typename Derived> 

      

        

          Derived& MatrixBase< Derived >::operator= 
          (
          const MatrixBase< Derived > & 
           other
           ) 
           [inline]
        

      






Special case of the template operator=, in order to prevent the compiler from generating a default operator= (issue hit with g++ 4.1) 



Definition at line 229 of file MatrixBase.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator= 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           [inline]
        

      






Copies other into *this. 


Returns:
a reference to *this. 



Reimplemented in MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 465 of file Assign.h.













template<typename Derived> 



template<typename OtherDerived > 

      

        

          bool MatrixBase< Derived >::operator== 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           const [inline]
        

      







Definition at line 475 of file MatrixBase.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE ei_traits< Derived >::Scalar & MatrixBase< Derived >::operator[] 
          (
          int 
           index
           ) 
           [inline]
        

      






Returns:
a reference to the coefficient at given index.


This method is allowed only for vector expressions, and for matrix expressions having the LinearAccessBit.


See also:
operator[](int) const, operator()(int,int), x(), y(), z(), w() 



Definition at line 184 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const ei_traits< Derived >::Scalar MatrixBase< Derived >::operator[] 
          (
          int 
           index
           ) 
           const [inline]
        

      






Returns:
the coefficient at given index.


This method is allowed only for vector expressions, and for matrix expressions having the LinearAccessBit.


See also:
operator[](int), operator()(int,int) const, x() const, y() const, z() const, w() const 



Definition at line 131 of file Coeffs.h.













template<typename Derived > 

      

        

          NumTraits< typename ei_traits< Derived >::Scalar >::Real MatrixBase< Derived >::operatorNorm 
          (
          
           ) 
           const [inline]
        

      






Returns:
the matrix norm of this matrix. 



Definition at line 335 of file SelfAdjointEigenSolver.h.













template<typename Derived> 

      

        

          int MatrixBase< Derived >::outerSize 
          (
          
           ) 
           const [inline]
        

      






Returns:
the size of the storage major dimension, i.e., the number of columns for a columns major matrix, and the number of rows otherwise 



Definition at line 170 of file MatrixBase.h.













template<typename Derived > 



template<int LoadMode> 

      

        

          EIGEN_STRONG_INLINE ei_packet_traits< typename ei_traits< Derived >::Scalar >::type MatrixBase< Derived >::packet 
          (
          int 
           index
           ) 
           const [inline]
        

      






Returns:
the packet of coefficients starting at the given index. It is your responsibility to ensure that a packet really starts there. This method is only available on expressions having the PacketAccessBit and the LinearAccessBit.


The LoadMode parameter may have the value Aligned or Unaligned. Its effect is to select the appropriate vectorization instruction. Aligned access is faster, but is only possible for packets starting at an address which is a multiple of the packet size. 



Reimplemented in Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, CwiseBinaryOp< BinaryOp, Lhs, Rhs >, CwiseNullaryOp< NullaryOp, MatrixType >, CwiseUnaryOp< UnaryOp, MatrixType >, Flagged< ExpressionType, Added, Removed >, MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, NestByValue< ExpressionType >, Transpose< MatrixType >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 293 of file Coeffs.h.













template<typename Derived > 



template<int LoadMode> 

      

        

          EIGEN_STRONG_INLINE ei_packet_traits< typename ei_traits< Derived >::Scalar >::type MatrixBase< Derived >::packet 
          (
          int 
           row, 
        

        

          
          
          int 
           col 
        

        

          
          )
           const [inline]
        

      






Returns:
the packet of coefficients starting at the given row and column. It is your responsibility to ensure that a packet really starts there. This method is only available on expressions having the PacketAccessBit.


The LoadMode parameter may have the value Aligned or Unaligned. Its effect is to select the appropriate vectorization instruction. Aligned access is faster, but is only possible for packets starting at an address which is a multiple of the packet size. 



Reimplemented in Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, CwiseBinaryOp< BinaryOp, Lhs, Rhs >, CwiseNullaryOp< NullaryOp, MatrixType >, CwiseUnaryOp< UnaryOp, MatrixType >, Product< LhsNested, RhsNested, DiagonalProduct >, Flagged< ExpressionType, Added, Removed >, MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, NestByValue< ExpressionType >, Product< LhsNested, RhsNested, ProductMode >, Transpose< MatrixType >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 257 of file Coeffs.h.













template<typename Derived > 



template<unsigned int Mode> 

      

        

          const Part< Derived, Mode > MatrixBase< Derived >::part 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of a triangular matrix extracted from the current matrix


The parameter Mode can have the following values: UpperTriangular, StrictlyUpperTriangular, UnitUpperTriangular, LowerTriangular, StrictlyLowerTriangular, UnitLowerTriangular.


PartExample  How to extract a triangular part of an arbitrary matrix


Example: 


 Output: 


See also:
class Part, part(), marked() 



Definition at line 148 of file Part.h.













template<typename Derived > 



template<unsigned int Mode> 

      

        

          Part< Derived, Mode > MatrixBase< Derived >::part 
          (
          
           ) 
           [inline]
        

      






Returns:
a lvalue pseudo-expression allowing to perform special operations on *this.


The Mode parameter can have the following values: UpperTriangular, StrictlyUpperTriangular, LowerTriangular, StrictlyLowerTriangular, SelfAdjoint.


PartExample  How to write to a triangular part of a matrix


Example: 


 Output: 


See also:
class Part, MatrixBase::extract(), MatrixBase::marked() 



Definition at line 300 of file Part.h.













template<typename Derived > 

      

        

          const QR< typename MatrixBase< Derived >::PlainMatrixType > MatrixBase< Derived >::qr 
          (
          
           ) 
           const [inline]
        

      






Returns:
the QR decomposition of *this.


See also:
class QR 



Definition at line 334 of file QR.h.













template<typename Derived > 

      

        

          const CwiseNullaryOp< ei_scalar_random_op< typename ei_traits< Derived >::Scalar >, Derived > MatrixBase< Derived >::Random 
          (
          
           ) 
           [inline, static]
        

      






Returns:
a fixed-size random matrix or vector (not an expression, the matrix is immediately evaluated).


This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.


Example: 


 Output: 


See also:
MatrixBase::setRandom(), MatrixBase::Random(int,int), MatrixBase::Random(int) 



Definition at line 101 of file Random.h.













template<typename Derived > 

      

        

          const CwiseNullaryOp< ei_scalar_random_op< typename ei_traits< Derived >::Scalar >, Derived > MatrixBase< Derived >::Random 
          (
          int 
           size
           ) 
           [inline, static]
        

      






Returns:
a random vector (not an expression, the vector is immediately evaluated).


The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so ei_random() should be used instead.


Example: 


 Output: 


See also:
MatrixBase::setRandom(), MatrixBase::Random(int,int), MatrixBase::Random() 



Definition at line 81 of file Random.h.













template<typename Derived > 

      

        

          const CwiseNullaryOp< ei_scalar_random_op< typename ei_traits< Derived >::Scalar >, Derived > MatrixBase< Derived >::Random 
          (
          int 
           rows, 
        

        

          
          
          int 
           cols 
        

        

          
          )
           [inline, static]
        

      






Returns:
a random matrix (not an expression, the matrix is immediately evaluated).


The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so ei_random() should be used instead.


RandomExample  How to create a matrix with random coefficients


Example: 


 Output: 


See also:
MatrixBase::setRandom(), MatrixBase::Random(int), MatrixBase::Random() 



Definition at line 56 of file Random.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::RealReturnType MatrixBase< Derived >::real 
          (
          
           ) 
           const [inline]
        

      






Returns:
an expression of the real part of *this.


See also:
imag() 



Definition at line 173 of file CwiseUnaryOp.h.













template<typename Derived > 

      

        

          const MatrixBase< Derived >::RowXpr MatrixBase< Derived >::row 
          (
          int 
           i
           ) 
           const [inline]
        

      






This is the const version of row(). 



Reimplemented in Part< MatrixType, Mode >.



Definition at line 747 of file Block.h.













template<typename Derived > 

      

        

          MatrixBase< Derived >::RowXpr MatrixBase< Derived >::row 
          (
          int 
           i
           ) 
           [inline]
        

      






Returns:
an expression of the i-th row of *this. Note that the numbering starts at 0.


BlockRow  How to reference a single row of a matrix


Example: 


 Output: 


See also:
col(), class Block 



Reimplemented in Part< MatrixType, Mode >.



Definition at line 739 of file Block.h.













template<typename Derived> 

      

        

          int MatrixBase< Derived >::rows 
          (
          
           ) 
           const [inline]
        

      






Returns:
the number of rows. 


See also:
cols(), RowsAtCompileTime 



Reimplemented in PartialReduxExpr< MatrixType, MemberOp, Direction >, Select< ConditionMatrixType, ThenMatrixType, ElseMatrixType >, Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, CwiseBinaryOp< BinaryOp, Lhs, Rhs >, CwiseNullaryOp< NullaryOp, MatrixType >, CwiseUnaryOp< UnaryOp, MatrixType >, DiagonalCoeffs< MatrixType >, DiagonalMatrix< CoeffsVectorType >, Product< LhsNested, RhsNested, DiagonalProduct >, Flagged< ExpressionType, Added, Removed >, MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, Minor< MatrixType >, NestByValue< ExpressionType >, Part< MatrixType, Mode >, Product< LhsNested, RhsNested, ProductMode >, SwapWrapper< ExpressionType >, Transpose< MatrixType >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 154 of file MatrixBase.h.













template<typename Derived > 

      

        

          const PartialRedux< Derived, Horizontal > MatrixBase< Derived >::rowwise 
          (
          
           ) 
           const [inline]
        

      






Returns:
a PartialRedux wrapper of *this providing additional partial reduction operations


Example: 


 Output: 


See also:
colwise(), class PartialRedux 



Definition at line 329 of file PartialRedux.h.













template<typename Derived > 



template<int Size> 

      

        

          const BlockReturnType< Derived, Size >::SubVectorType MatrixBase< Derived >::segment 
          (
          int 
           start
           ) 
           const [inline]
        

      






This is the const version of segment<int>(int). 



Definition at line 480 of file Block.h.













template<typename Derived > 



template<int Size> 

      

        

          BlockReturnType< Derived, Size >::SubVectorType MatrixBase< Derived >::segment 
          (
          int 
           start
           ) 
           [inline]
        

      






Returns:
a fixed-size expression of a segment (i.e. a vector block) in *this 


The template parameter Size is the number of coefficients in the block


Parameters:

  

    
start the index of the first element of the sub-vector

  

  




Example: 


 Output: 


See also:
class Block 



Definition at line 467 of file Block.h.













template<typename Derived > 

      

        

          const BlockReturnType< Derived >::SubVectorType MatrixBase< Derived >::segment 
          (
          int 
           start, 
        

        

          
          
          int 
           size 
        

        

          
          )
           const [inline]
        

      






This is the const version of segment(int,int). 



Definition at line 350 of file Block.h.













template<typename Derived > 

      

        

          BlockReturnType< Derived >::SubVectorType MatrixBase< Derived >::segment 
          (
          int 
           start, 
        

        

          
          
          int 
           size 
        

        

          
          )
           [inline]
        

      






Returns:
a dynamic-size expression of a segment (i.e. a vector block) in *this.


SegmentIntInt  How to reference a sub-vector (dynamic size)


Parameters:

  

    
start the first coefficient in the segment 

    
size the number of coefficients in the segment

  

  




Example: 


 Output: 


Note:
Even though the returned expression has dynamic size, in the case when it is applied to a fixed-size vector, it inherits a fixed maximal size, which means that evaluating it does not cause a dynamic memory allocation.


See also:
class Block, segment(int) 



Definition at line 338 of file Block.h.













template<typename Derived > 



template<typename ElseDerived > 

      

        

          const Select< Derived, NestByValue< typename ElseDerived::ConstantReturnType >, ElseDerived > MatrixBase< Derived >::select 
          (
          typename ElseDerived::Scalar 
           thenScalar, 
        

        

          
          
          const MatrixBase< ElseDerived > & 
           elseMatrix 
        

        

          
          )
           const [inline]
        

      






Version of MatrixBase::select(const MatrixBase&, const MatrixBase&) with the then expression being a scalar value.


See also:
MatrixBase::select(const MatrixBase<ThenDerived>&, const MatrixBase<ElseDerived>&) const, class Select 



Definition at line 152 of file Select.h.













template<typename Derived > 



template<typename ThenDerived > 

      

        

          const Select< Derived, ThenDerived, NestByValue< typename ThenDerived::ConstantReturnType > > MatrixBase< Derived >::select 
          (
          const MatrixBase< ThenDerived > & 
           thenMatrix, 
        

        

          
          
          typename ThenDerived::Scalar 
           elseScalar 
        

        

          
          )
           const [inline]
        

      






Version of MatrixBase::select(const MatrixBase&, const MatrixBase&) with the else expression being a scalar value.


See also:
MatrixBase::select(const MatrixBase<ThenDerived>&, const MatrixBase<ElseDerived>&) const, class Select 



Definition at line 135 of file Select.h.













template<typename Derived > 



template<typename ThenDerived , typename ElseDerived > 

      

        

          const Select< Derived, ThenDerived, ElseDerived > MatrixBase< Derived >::select 
          (
          const MatrixBase< ThenDerived > & 
           thenMatrix, 
        

        

          
          
          const MatrixBase< ElseDerived > & 
           elseMatrix 
        

        

          
          )
           const [inline]
        

      






Returns:
a matrix where each coefficient (i,j) is equal to thenMatrix(i,j) if *this(i,j), and elseMatrix(i,j) otherwise.


Example: 


 Output: 


See also:
class Select 



Definition at line 119 of file Select.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::setConstant 
          (
          const Scalar & 
           value
           ) 
           [inline]
        

      






Sets all coefficients in this expression to value.


See also:
fill(), setConstant(int,const Scalar&), setConstant(int,int,const Scalar&), setZero(), setOnes(), Constant(), class CwiseNullaryOp, setZero(), setOnes() 



Definition at line 268 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::setIdentity 
          (
          
           ) 
           [inline]
        

      






Writes the identity expression (not necessarily square) into *this.


Example: 


 Output: 


See also:
class CwiseNullaryOp, Identity(), Identity(int,int), isIdentity() 



Definition at line 672 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::setOnes 
          (
          
           ) 
           [inline]
        

      






Sets all coefficients in this expression to one.


Example: 


 Output: 


See also:
class CwiseNullaryOp, Ones() 



Definition at line 528 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          Derived & MatrixBase< Derived >::setRandom 
          (
          
           ) 
           [inline]
        

      






Sets all coefficients in this expression to random values.


Example: 


 Output: 


See also:
class CwiseNullaryOp, setRandom(int), setRandom(int,int) 



Definition at line 116 of file Random.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::setZero 
          (
          
           ) 
           [inline]
        

      






Sets all coefficients in this expression to zero.


Example: 


 Output: 


See also:
class CwiseNullaryOp, Zero() 



Definition at line 400 of file CwiseNullaryOp.h.













template<typename Derived> 

      

        

          int MatrixBase< Derived >::size 
          (
          
           ) 
           const [inline]
        

      






Returns:
the number of coefficients, which is rows()*cols(). 


See also:
rows(), cols(), SizeAtCompileTime. 



Definition at line 159 of file MatrixBase.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          ei_plain_matrix_type_column_major< OtherDerived >::type MatrixBase< Derived >::solveTriangular 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           const [inline]
        

      






Returns:
the product of the inverse of *this with other, *this being triangular.


This function computes the inverse-matrix matrix product inverse(*this) * other. The matrix *this must be triangular and invertible (i.e., all the coefficients of the diagonal must be non zero). It works as a forward (resp. backward) substitution if *this is an upper (resp. lower) triangular matrix.


It is required that *this be marked as either an upper or a lower triangular matrix, which can be done by marked(), and that is automatically the case with expressions such as those returned by extract().


SolveTriangular  How to solve a triangular system (aka. how to multiply the inverse of a triangular matrix by another one)


Example: 


 Output: 


This function is essentially a wrapper to the faster solveTriangularInPlace() function creating a temporary copy of other, calling solveTriangularInPlace() on the copy and returning it. Therefore, if other is not needed anymore, it is quite faster to call solveTriangularInPlace() instead of solveTriangular().


For users coming from BLAS, this function (and more specifically solveTriangularInPlace()) offer all the operations supported by the *TRSV and *TRSM BLAS routines.


Tips: to perform a "right-inverse-multiply" you can simply transpose the operation, e.g.: 


 M * T^1  <=>  T.transpose().solveTriangularInPlace(M.transpose());

See also:
solveTriangularInPlace(), marked(), extract() 



Definition at line 290 of file SolveTriangular.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          void MatrixBase< Derived >::solveTriangularInPlace 
          (
          const MatrixBase< OtherDerived > & 
           _other
           ) 
           const [inline]
        

      






"in-place" version of MatrixBase::solveTriangular() where the result is written in other 


The parameter is only marked 'const' to make the C++ compiler accept a temporary expression here. This function will const_cast it, so constness isn't honored here.


See MatrixBase:solveTriangular() for the details. 



Definition at line 234 of file SolveTriangular.h.













template<typename Derived > 

      

        

          NumTraits< typename ei_traits< Derived >::Scalar >::Real MatrixBase< Derived >::squaredNorm 
          (
          
           ) 
           const [inline]
        

      






Returns:
the squared l2 norm of *this, i.e., for vectors, the dot product of *this with itself.


See also:
dot(), norm() 



Definition at line 277 of file Dot.h.













template<typename Derived> 



template<int Size> 

      

        

          const BlockReturnType<Derived,Size>::SubVectorType MatrixBase< Derived >::start 
          (
          
           ) 
           const [inline]
        

      

















template<typename Derived > 



template<int Size> 

      

        

          const BlockReturnType< Derived, Size >::SubVectorType MatrixBase< Derived >::start 
          (
          void 
          
           ) 
           [inline]
        

      






Returns:
a fixed-size expression of the first coefficients of *this.


The template parameter Size is the number of coefficients in the block


BlockStart  How to reference the start of a vector (fixed-size)


Example: 


 Output: 


See also:
class Block


This is the const version of start<int>(). 



Definition at line 505 of file Block.h.













template<typename Derived > 

      

        

          const BlockReturnType< Derived, Dynamic >::SubVectorType MatrixBase< Derived >::start 
          (
          int 
           size
           ) 
           const [inline]
        

      






This is the const version of start(int). 



Definition at line 392 of file Block.h.













template<typename Derived > 

      

        

          BlockReturnType< Derived, Dynamic >::SubVectorType MatrixBase< Derived >::start 
          (
          int 
           size
           ) 
           [inline]
        

      






Returns:
a dynamic-size expression of the first coefficients of *this.


Parameters:

  

    
size the number of coefficients in the block

  

  




BlockInt  How to reference a sub-vector (fixed-size)


Example: 


 Output: 


Note:
Even though the returned expression has dynamic size, in the case when it is applied to a fixed-size vector, it inherits a fixed maximal size, which means that evaluating it does not cause a dynamic memory allocation.


See also:
class Block, block(int,int) 



Definition at line 378 of file Block.h.













template<typename Derived> 

      

        

          int MatrixBase< Derived >::stride 
          (
          void 
          
           ) 
           const [inline]
        

      






Returns:
number of elements to skip to pass from one row (resp. column) to another for a row-major (resp. column-major) matrix. Combined with coeffRef() and the flags flags, it allows a direct access to the data of the underlying matrix. 



Reimplemented in Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess >, Flagged< ExpressionType, Added, Removed >, Map< MatrixType, PacketAccess >, MapBase< Derived >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, NestByValue< ExpressionType >, Part< MatrixType, Mode >, SwapWrapper< ExpressionType >, Transpose< MatrixType >, MapBase< Block< MatrixType, BlockRows, BlockCols, PacketAccess, HasDirectAccess > >, MapBase< Map< MatrixType, PacketAccess > >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 506 of file MatrixBase.h.













template<typename Derived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::sum 
          (
          
           ) 
           const [inline]
        

      






Returns:
the sum of all coefficients of *this


See also:
trace() 



Definition at line 253 of file Sum.h.













template<typename Derived > 

      

        

          SVD< typename MatrixBase< Derived >::PlainMatrixType > MatrixBase< Derived >::svd 
          (
          
           ) 
           const [inline]
        

      






Returns:
the SVD decomposition of *this 



Definition at line 644 of file SVD.h.













template<typename Derived > 



template<typename OtherDerived > 

      

        

          void MatrixBase< Derived >::swap 
          (
          const MatrixBase< OtherDerived > & 
           other
           ) 
           [inline]
        

      






swaps *this with the expression other.


Note:
other is only marked for internal reasons, but of course it gets const-casted. One reason is that one will often call swap on temporary objects (hence non-const references are forbidden). Another reason is that lazyAssign takes a const argument anyway. 



Reimplemented in Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, Part< MatrixType, Mode >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.



Definition at line 134 of file Swap.h.













template<typename Derived > 

      

        

          ei_traits< Derived >::Scalar MatrixBase< Derived >::trace 
          (
          
           ) 
           const [inline]
        

      






Returns:
the trace of *this, i.e. the sum of the coefficients on the main diagonal.


*this can be any matrix, not necessarily square.


See also:
diagonal(), sum() 



Definition at line 266 of file Sum.h.













template<typename Derived > 

      

        

          const Transpose< Derived > MatrixBase< Derived >::transpose 
          (
          
           ) 
           const [inline]
        

      






This is the const version of transpose().


Make sure you read the warning for transpose() !


See also:
transposeInPlace(), adjoint() 



Definition at line 155 of file Transpose.h.













template<typename Derived > 

      

        

          Transpose< Derived > MatrixBase< Derived >::transpose 
          (
          
           ) 
           [inline]
        

      






Returns:
an expression of the transpose of *this.


Example: 


 Output: 


Warning:
If you want to replace a matrix by its own transpose, do NOT do this: 
 m = m.transpose(); // bug!!! caused by aliasing effect

 Instead, use the transposeInPlace() method: 
 m.transposeInPlace();

 which gives Eigen good opportunities for optimization, or alternatively you can also do: 
 m = m.transpose().eval();



See also:
transposeInPlace(), adjoint() 



Definition at line 143 of file Transpose.h.













template<typename Derived > 

      

        

          void MatrixBase< Derived >::transposeInPlace 
          (
          
           ) 
           [inline]
        

      






This is the "in place" version of transpose: it transposes *this.


In most cases it is probably better to simply use the transposed expression of a matrix. However, when transposing the matrix data itself is really needed, then this "in-place" version is probably the right choice because it provides the following additional features:


    

  • less error prone: doing the same operation with .transpose() requires special care: 
     m = m.transpose().eval(); 

    • 

  • no temporary object is created (currently only for squared matrices)
    • 

  • it allows future optimizations (cache friendliness, etc.)
    • 



Note:
if the matrix is not square, then *this must be a resizable matrix.


See also:
transpose(), adjoint() 



Definition at line 222 of file Transpose.h.













template<typename Derived > 



template<typename CustomUnaryOp > 

      

        

          EIGEN_STRONG_INLINE const CwiseUnaryOp< CustomUnaryOp, Derived > MatrixBase< Derived >::unaryExpr 
          (
          const CustomUnaryOp & 
           func = CustomUnaryOp()
           ) 
           const [inline]
        

      






Returns:
an expression of a custom coefficient-wise unary operator func of *this


The template parameter CustomUnaryOp is the type of the functor of the custom unary operator.


CustomCwiseUnaryFunctors  How to use custom coeff wise unary functors


Example: 


 Output: 


See also:
class CwiseUnaryOp, class CwiseBinarOp, MatrixBase::operator-, Cwise::abs 



Definition at line 116 of file CwiseUnaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::Unit 
          (
          int 
           i
           ) 
           [inline, static]
        

      






Returns:
an expression of the i-th unit (basis) vector.


This variant is for fixed-size vector only.


See also:
MatrixBase::Unit(int,int), MatrixBase::UnitX(), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW() 



Definition at line 717 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::Unit 
          (
          int 
           size, 
        

        

          
          
          int 
           i 
        

        

          
          )
           [inline, static]
        

      






Returns:
an expression of the i-th unit (basis) vector.


See also:
MatrixBase::Unit(int), MatrixBase::UnitX(), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW() 



Definition at line 702 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          MatrixBase< Derived >::PlainMatrixType MatrixBase< Derived >::unitOrthogonal 
          (
          void 
          
           ) 
           const [inline]
        

      






Returns:
a unit vector which is orthogonal to *this 


The size of *this must be at least 2. If the size is exactly 2, then the returned vector is a counter clock wise rotation of *this, i.e., (-y,x).normalized().


See also:
cross() 



Definition at line 113 of file OrthoMethods.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::UnitW 
          (
          
           ) 
           [inline, static]
        

      






Returns:
an expression of the W axis unit vector (0,0,0,1)


See also:
MatrixBase::Unit(int,int), MatrixBase::Unit(int), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW() 



Definition at line 760 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::UnitX 
          (
          
           ) 
           [inline, static]
        

      






Returns:
an expression of the X axis unit vector (1{,0}^*)


See also:
MatrixBase::Unit(int,int), MatrixBase::Unit(int), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW() 



Definition at line 730 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::UnitY 
          (
          
           ) 
           [inline, static]
        

      






Returns:
an expression of the Y axis unit vector (0,1{,0}^*)


See also:
MatrixBase::Unit(int,int), MatrixBase::Unit(int), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW() 



Definition at line 740 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::UnitZ 
          (
          
           ) 
           [inline, static]
        

      






Returns:
an expression of the Z axis unit vector (0,0,1{,0}^*)


See also:
MatrixBase::Unit(int,int), MatrixBase::Unit(int), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW() 



Definition at line 750 of file CwiseNullaryOp.h.













template<typename Derived > 



template<typename Visitor > 

      

        

          void MatrixBase< Derived >::visit 
          (
          Visitor & 
           visitor
           ) 
           const [inline]
        

      






Applies the visitor visitor to the whole coefficients of the matrix or vector.


The template parameter Visitor is the type of the visitor and provides the following interface: 


 struct MyVisitor {
   // called for the first coefficient
   void init(const Scalar& value, int i, int j);
   // called for all other coefficients
   void operator() (const Scalar& value, int i, int j);
 };

Note:
compared to one or two for loops, visitors offer automatic unrolling for small fixed size matrix.


See also:
minCoeff(int*,int*), maxCoeff(int*,int*), MatrixBase::redux() 



Definition at line 86 of file Visitor.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE ei_traits< Derived >::Scalar & MatrixBase< Derived >::w 
          (
          
           ) 
           [inline]
        

      






equivalent to operator[](3). 



Definition at line 244 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const ei_traits< Derived >::Scalar MatrixBase< Derived >::w 
          (
          
           ) 
           const [inline]
        

      






equivalent to operator[](3). 



Definition at line 224 of file Coeffs.h.













template<typename Derived> 



template<int StoreMode> 

      

        

          EIGEN_STRONG_INLINE void MatrixBase< Derived >::writePacket 
          (
          int 
           index, 
        

        

          
          
          const typename ei_packet_traits< typename ei_traits< Derived >::Scalar >::type & 
           x 
        

        

          
          )
           [inline]
        

      






Stores the given packet of coefficients, at the given index in this expression. It is your responsibility to ensure that a packet really starts there. This method is only available on expressions having the PacketAccessBit and the LinearAccessBit.


The LoadMode parameter may have the value Aligned or Unaligned. Its effect is to select the appropriate vectorization instruction. Aligned access is faster, but is only possible for packets starting at an address which is a multiple of the packet size. 



Definition at line 310 of file Coeffs.h.













template<typename Derived> 



template<int StoreMode> 

      

        

          EIGEN_STRONG_INLINE void MatrixBase< Derived >::writePacket 
          (
          int 
           row, 
        

        

          
          
          int 
           col, 
        

        

          
          
          const typename ei_packet_traits< typename ei_traits< Derived >::Scalar >::type & 
           x 
        

        

          
          )
           [inline]
        

      






Stores the given packet of coefficients, at the given row and column of this expression. It is your responsibility to ensure that a packet really starts there. This method is only available on expressions having the PacketAccessBit.


The LoadMode parameter may have the value Aligned or Unaligned. Its effect is to select the appropriate vectorization instruction. Aligned access is faster, but is only possible for packets starting at an address which is a multiple of the packet size. 



Definition at line 275 of file Coeffs.h.













template<typename Derived> 



template<int StoreMode> 

      

        

          void MatrixBase< Derived >::writePacket 
          (
          int 
           index, 
        

        

          
          
          const PacketScalar & 
           x 
        

        

          
          )
           [inline]
        

      







Reimplemented in Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, Flagged< ExpressionType, Added, Removed >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, NestByValue< ExpressionType >, Transpose< MatrixType >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.













template<typename Derived> 



template<int StoreMode> 

      

        

          void MatrixBase< Derived >::writePacket 
          (
          int 
           row, 
        

        

          
          
          int 
           col, 
        

        

          
          
          const PacketScalar & 
           x 
        

        

          
          )
           [inline]
        

      







Reimplemented in Block< MatrixType, BlockRows, BlockCols, PacketAccess, _DirectAccessStatus >, Flagged< ExpressionType, Added, Removed >, Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >, NestByValue< ExpressionType >, Transpose< MatrixType >, Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize >, Matrix< int, 1, MatrixType::ColsAtCompileTime >, Matrix< int, MatrixType::RowsAtCompileTime, 1 >, Matrix< Scalar, 4, 1 >, Matrix< Scalar, HDim, HDim >, Matrix< Complex, MatrixType::ColsAtCompileTime, 1 >, Matrix< Scalar, 3, 1 >, Matrix< int, 1, MatrixType::ColsAtCompileTime, MatrixType::Options, 1, MatrixType::MaxColsAtCompileTime >, Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime >, Matrix< Scalar, Dim, 1 >, Matrix< Scalar, MinSize, 1 >, Matrix< Scalar, SizeMinusOne, 1 >, Matrix< int, MatrixType::RowsAtCompileTime, 1, MatrixType::Options, MatrixType::MaxRowsAtCompileTime, 1 >, Matrix< Scalar, int(AmbientDimAtCompileTime)==Dynamic?Dynamic:int(AmbientDimAtCompileTime)+1, 1 >, Matrix< Scalar, AmbientDimAtCompileTime, 1 >, Matrix< RealScalar, MatrixType::ColsAtCompileTime, 1 >, and Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 >.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE ei_traits< Derived >::Scalar & MatrixBase< Derived >::x 
          (
          
           ) 
           [inline]
        

      






equivalent to operator[](0). 



Definition at line 229 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const ei_traits< Derived >::Scalar MatrixBase< Derived >::x 
          (
          
           ) 
           const [inline]
        

      






equivalent to operator[](0). 



Definition at line 209 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE ei_traits< Derived >::Scalar & MatrixBase< Derived >::y 
          (
          
           ) 
           [inline]
        

      






equivalent to operator[](1). 



Definition at line 234 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const ei_traits< Derived >::Scalar MatrixBase< Derived >::y 
          (
          
           ) 
           const [inline]
        

      






equivalent to operator[](1). 



Definition at line 214 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE ei_traits< Derived >::Scalar & MatrixBase< Derived >::z 
          (
          
           ) 
           [inline]
        

      






equivalent to operator[](2). 



Definition at line 239 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const ei_traits< Derived >::Scalar MatrixBase< Derived >::z 
          (
          
           ) 
           const [inline]
        

      






equivalent to operator[](2). 



Definition at line 219 of file Coeffs.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ConstantReturnType MatrixBase< Derived >::Zero 
          (
          
           ) 
           [inline, static]
        

      






Returns:
an expression of a fixed-size zero matrix or vector.


This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.


Example: 


 Output: 


See also:
Zero(int), Zero(int,int) 



Definition at line 369 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ConstantReturnType MatrixBase< Derived >::Zero 
          (
          int 
           size
           ) 
           [inline, static]
        

      






Returns:
an expression of a zero vector.


The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.


Example: 


 Output: 


See also:
Zero(), Zero(int,int) 



Definition at line 352 of file CwiseNullaryOp.h.













template<typename Derived > 

      

        

          EIGEN_STRONG_INLINE const MatrixBase< Derived >::ConstantReturnType MatrixBase< Derived >::Zero 
          (
          int 
           rows, 
        

        

          
          
          int 
           cols 
        

        

          
          )
           [inline, static]
        

      






Returns:
an expression of a zero matrix.


The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.


This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.


Zero  How to take get a zero matrix


Example: 


 Output: 


See also:
Zero(), Zero(int) 



Definition at line 329 of file CwiseNullaryOp.h.







Friends And Related Function Documentation








template<typename Derived> 

      

        

          const CwiseUnaryOp<ei_scalar_multiple_op<typename ei_traits<Derived>::Scalar>, Derived> operator* 
          (
          const Scalar & 
           scalar, 
        

        

          
          
          const MatrixBase< Derived > & 
           matrix 
        

        

          
          )
           [friend]
        

      







Definition at line 325 of file MatrixBase.h.













template<typename Derived > 

      

        

          std::ostream & operator<< 
          (
          std::ostream & 
           s, 
        

        

          
          
          const MatrixBase< Derived > & 
           m 
        

        

          
          )
           [related]
        

      






Outputs the matrix, to the given stream.


If you wish to print the matrix with a format different than the default, use MatrixBase::format().


It is also possible to change the default format by defining EIGEN_DEFAULT_IO_FORMAT before including Eigen headers. If not defined, this will automatically be defined to Eigen::IOFormat(), that is the Eigen::IOFormat with default parameters.


See also:
MatrixBase::format() 



Definition at line 178 of file IO.h.







The documentation for this class was generated from the following files:





 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Defines














vcglib

Author(s): Christian Bersch

autogenerated on Fri Jan 11 09:22:08 2013