Robust Cholesky decomposition of a matrix and associated features. More...
#include <LDLT.h>
Public Types | |
| typedef NumTraits< typename MatrixType::Scalar >::Real | RealScalar |
| typedef MatrixType::Scalar | Scalar |
| typedef Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 > | VectorType |
Public Member Functions | |
| void | compute (const MatrixType &matrix) |
| bool | isPositiveDefinite (void) const |
| LDLT (const MatrixType &matrix) | |
| Part< MatrixType, UnitLowerTriangular > | matrixL (void) const |
| template<typename RhsDerived , typename ResultType > | |
| bool | solve (const MatrixBase< RhsDerived > &b, ResultType *result) const |
| template<typename Derived > | |
| bool | solveInPlace (MatrixBase< Derived > &bAndX) const |
| DiagonalCoeffs< MatrixType > | vectorD (void) const |
Protected Attributes | |
| bool | m_isPositiveDefinite |
| MatrixType | m_matrix |
Robust Cholesky decomposition of a matrix and associated features.
| MatrixType | the type of the matrix of which we are computing the LDL^T Cholesky decomposition |
This class performs a Cholesky decomposition without square root of a symmetric, positive definite matrix A such that A = L D L^* = U^* D U, where L is lower triangular with a unit diagonal and D is a diagonal matrix.
Compared to a standard Cholesky decomposition, avoiding the square roots allows for faster and more stable computation.
Note that during the decomposition, only the upper triangular part of A is considered. Therefore, the strict lower part does not have to store correct values.
Definition at line 48 of file LDLT.h.
| typedef NumTraits<typename MatrixType::Scalar>::Real LDLT< MatrixType >::RealScalar |
| typedef Matrix<Scalar, MatrixType::ColsAtCompileTime, 1> LDLT< MatrixType >::VectorType |
| void LDLT< MatrixType >::compute | ( | const MatrixType & | a | ) | [inline] |
| bool LDLT< MatrixType >::isPositiveDefinite | ( | void | ) | const [inline] |
| Part<MatrixType, UnitLowerTriangular> LDLT< MatrixType >::matrixL | ( | void | ) | const [inline] |
| bool LDLT< MatrixType >::solve | ( | const MatrixBase< RhsDerived > & | b, | |
| ResultType * | result | |||
| ) | const [inline] |
Computes the solution x of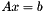 
using the current decomposition of A. The result is stored in result
In other words, it computes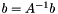 
with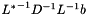 
from right to left.
| bool LDLT< MatrixType >::solveInPlace | ( | MatrixBase< Derived > & | bAndX | ) | const [inline] |
This is the in-place version of solve().
| bAndX | represents both the right-hand side matrix b and result x. |
This version avoids a copy when the right hand side matrix b is not needed anymore.
| DiagonalCoeffs<MatrixType> LDLT< MatrixType >::vectorD | ( | void | ) | const [inline] |
bool LDLT< MatrixType >::m_isPositiveDefinite [protected] |
