Standard Cholesky decomposition (LL^T) of a matrix and associated features. More...
#include <LLT.h>
Public Member Functions | |
| void | compute (const MatrixType &matrix) |
| bool | isPositiveDefinite (void) const |
| LLT (const MatrixType &matrix) | |
| LLT () | |
| Default Constructor. | |
| Part< MatrixType, LowerTriangular > | matrixL (void) const |
| template<typename RhsDerived , typename ResultType > | |
| bool | solve (const MatrixBase< RhsDerived > &b, ResultType *result) const |
| template<typename Derived > | |
| bool | solveInPlace (MatrixBase< Derived > &bAndX) const |
Protected Attributes | |
| bool | m_isInitialized |
| bool | m_isPositiveDefinite |
| MatrixType | m_matrix |
Private Types | |
| enum | { PacketSize = ei_packet_traits<Scalar>::size, AlignmentMask = int(PacketSize)-1 } |
| typedef NumTraits< typename MatrixType::Scalar >::Real | RealScalar |
| typedef MatrixType::Scalar | Scalar |
| typedef Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 > | VectorType |
Standard Cholesky decomposition (LL^T) of a matrix and associated features.
| MatrixType | the type of the matrix of which we are computing the LL^T Cholesky decomposition |
This class performs a LL^T Cholesky decomposition of a symmetric, positive definite matrix A such that A = LL^* = U^*U, where L is lower triangular.
While the Cholesky decomposition is particularly useful to solve selfadjoint problems like D^*D x = b, for that purpose, we recommend the Cholesky decomposition without square root which is more stable and even faster. Nevertheless, this standard Cholesky decomposition remains useful in many other situations like generalised eigen problems with hermitian matrices.
Remember that Cholesky decompositions are not rank-revealing. This LLT decomposition is only stable on positive definite matrices, use LDLT instead for the semidefinite case. Also, do not use a Cholesky decomposition to determine whether a system of equations has a solution.
Definition at line 54 of file LLT.h.
typedef NumTraits<typename MatrixType::Scalar>::Real LLT< MatrixType >::RealScalar [private] |
typedef Matrix<Scalar, MatrixType::ColsAtCompileTime, 1> LLT< MatrixType >::VectorType [private] |
anonymous enum [private] |
Default Constructor.
The default constructor is useful in cases in which the user intends to perform decompositions via LLT::compute(const MatrixType&).
| void LLT< MatrixType >::compute | ( | const MatrixType & | a | ) | [inline] |
| bool LLT< MatrixType >::isPositiveDefinite | ( | void | ) | const [inline] |
| Part<MatrixType, LowerTriangular> LLT< MatrixType >::matrixL | ( | void | ) | const [inline] |
| bool LLT< MatrixType >::solve | ( | const MatrixBase< RhsDerived > & | b, | |
| ResultType * | result | |||
| ) | const [inline] |
Computes the solution x of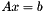 
using the current decomposition of A. The result is stored in result
In other words, it computes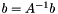 
with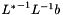 
from right to left.
Example:
Output:
| bool LLT< MatrixType >::solveInPlace | ( | MatrixBase< Derived > & | bAndX | ) | const [inline] |
This is the in-place version of solve().
| bAndX | represents both the right-hand side matrix b and result x. |
This version avoids a copy when the right hand side matrix b is not needed anymore.
bool LLT< MatrixType >::m_isInitialized [protected] |
bool LLT< MatrixType >::m_isPositiveDefinite [protected] |
