Table of Contents
This tutorial explains how to setup a simple Process for MPC simulations. As a guiding example, we consider a simple actively damped quarter car model.
A Guiding Example: Simulation of a Quarter Car
In this section we consider a first principle quarter car model with active suspension. The four differential states of this model xB , vB , xW , and vW are the position/velocity of the body/wheel, respectively. Our control input is a limited damping force F acting between the body and the wheel. The road, denoted by the variable R , is considered as an (unknown) external disturbance. The dynamic equations have the following form:
![\[ f: \quad \left( \begin{array}{c} \dot{x}_\textrm{B}(t) \\ \dot{x}_\textrm{W}(t) \\ \dot{v}_\textrm{B}(t) \\ \dot{v}_\textrm{W}(t) \\ \end{array} \right) = \left( \begin{array}{c} v_\textrm{B}(t) \\ v_\textrm{W}(t) \\ \frac{1}{m_\textrm{B}} (-k_\textrm{S} s_\textrm{B}(t) + k_\textrm{S} x_\textrm{W}(t) + F(t))\\ \frac{1}{m_\textrm{W}} (-k_\textrm{T} x_\textrm{B}(t) - (k_\textrm{T} + k_\textrm{S})x_\textrm{W}(t) + k_\textrm{T} R(t) - F(t)) \end{array} \right) \]](form_62.png)
Within our simulation, we start at xB = 0.01 and all other states at zero. Moreover, we treat the mass of the body mB as manipulatable (time-constant) parameter, whereas fixed values are assigned to all other quantities.
In order to illustrate the concept, let us assume that not all states can be measured directly but only the first one together with a combination of the third one and the control input. For realizing this, we introduce the following output function:
![\[ g: \quad \left( \begin{array}{c} g_1( t ) \\ g_2( t ) \end{array} \right) = \left( \begin{array}{c} x_\textrm{B}(t) \\ 500 v_\textrm{B}(t) + F( t ) \end{array} \right) \]](form_63.png)
Basic Implementation of a Process for MPC Simulations in ACADO
The following piece of code shows how to implement a Process simulation based on this quarter car model. It comprises four main steps:
- Introducing all variables and constants.
- Setting up the quarter car ODE model together with the output function; these two functions form the DynamicSystem used for the Process simulation. (In case you do not define an output function, the Process output will be all differential states.)
- Setting up the Process, which comprises at least to define a dynamic system to be used for simulation together with the information which integrator is to be used. In our example, also integrator options are set, initial values for the differential states are defined and a plot window is specified. As the dynamic system of the quarter car comprises an external disturbance, we also have to specify values for it. This is done by reading the disturbance data from the file "road.txt".
- Simulating the Process by first initializing it, passing the start time of the simulation (otherwise simulation starts at 0.0), and second run it with given values for the control input and the parameter input. Afterwards, results can be obtained and are plotted according to the previously flushed plot window.
The file "road.txt" containing the disturbance data:
If we run the above piece of code in ACADO, the corresponding Gnuplot output should be as follows:
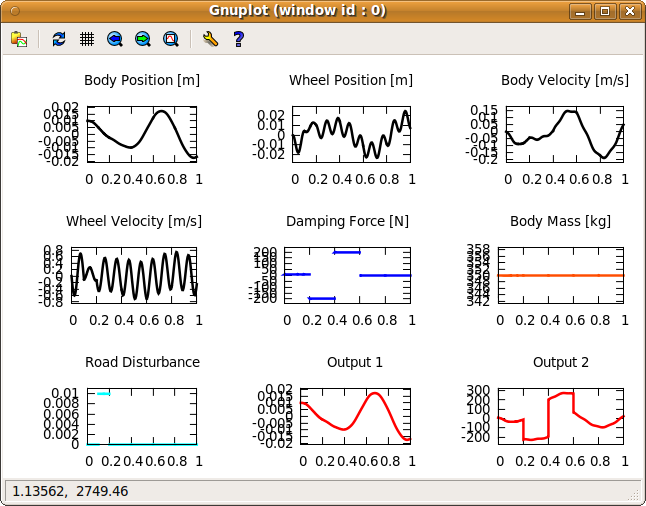
Note that this is only a simulation with user-specified control inputs; no feedback control is applied.
Obtaining the Simulation Results
We end this tutorial with proving a list of all results that can be obtained from the Process after simulation:
| Logging Name: | Short Description: |
| LOG_PROCESS_OUTPUT | All process outputs as specified via the output function |
| LOG_SIMULATED_DIFFERENTIAL_STATES | All differential states as simulated within the Process |
| LOG_SIMULATED_ALGEBRAIC_STATES | All algebraic states as simulated within the Process |
| LOG_SIMULATED_CONTROLS | All control inputs as simulated within the Process |
| LOG_SIMULATED_PARAMETERS | All parameter inputs as simulated within the Process |
| LOG_SIMULATED_DISTURBANCES | All external disturbances as simulated within the Process |
| LOG_NOMINAL_CONTROLS | All nominal control inputs as given to the Process |
| LOG_NOMINAL_PARAMETERS | All nominal parameter inputs as given to the Process |
Next example: Advanced Features for Simulating a Process