Gaussian Mixture Models - Implementation. More...
#include "gmm.h"#include <stdio.h>#include <stdlib.h>#include <string.h>#include "mathop_sse2.h"#include "mathop_avx.h"#include "shuffle-def.h"#include "gmm.c"

Go to the source code of this file.
Classes | |
| struct | _VlGMM |
Defines | |
| #define | FLT VL_TYPE_FLOAT |
| #define | FLT VL_TYPE_DOUBLE |
| #define | SFX f |
| #define | SFX d |
| #define | TYPE float |
| #define | TYPE double |
| #define | VL_GMM_INSTANTIATING |
| #define | VL_GMM_INSTANTIATING |
| #define | VL_GMM_MIN_POSTERIOR 1e-2 |
| #define | VL_GMM_MIN_PRIOR 1e-6 |
| #define | VL_GMM_MIN_VARIANCE 1e-6 |
| #define | VL_SHUFFLE_prefix _vl_gmm |
| #define | VL_SHUFFLE_type vl_uindex |
Functions | |
| static void | _vl_gmm_prepare_for_data (VlGMM *self, vl_size numData) |
| void | vl_gmm_delete (VlGMM *self) |
| Deletes a GMM object. | |
| double const * | vl_gmm_get_covariance_lower_bounds (VlGMM const *self) |
| Get the lower bound on the diagonal covariance values. | |
| void const * | vl_gmm_get_covariances (VlGMM const *self) |
| Get covariances. | |
| vl_type | vl_gmm_get_data_type (VlGMM const *self) |
| Get data type. | |
| vl_size | vl_gmm_get_dimension (VlGMM const *self) |
| Get data dimension. | |
| VlGMMInitialization | vl_gmm_get_initialization (VlGMM const *self) |
| Get initialization algorithm. | |
| VlKMeans * | vl_gmm_get_kmeans_init_object (VlGMM const *self) |
| Get KMeans initialization object. | |
| double | vl_gmm_get_loglikelihood (VlGMM const *self) |
| Get the log likelihood of the current mixture. | |
| vl_size | vl_gmm_get_max_num_iterations (VlGMM const *self) |
| Get maximum number of iterations. | |
| void const * | vl_gmm_get_means (VlGMM const *self) |
| Get means. | |
| vl_size | vl_gmm_get_num_clusters (VlGMM const *self) |
| Get the number of clusters. | |
| vl_size | vl_gmm_get_num_data (VlGMM const *self) |
| Get the number of data points. | |
| void const * | vl_gmm_get_posteriors (VlGMM const *self) |
| Get posteriors. | |
| void const * | vl_gmm_get_priors (VlGMM const *self) |
| Get priors. | |
| int | vl_gmm_get_verbosity (VlGMM const *self) |
| Get verbosity level. | |
| VlGMM * | vl_gmm_new (vl_type dataType, vl_size dimension, vl_size numComponents) |
| Create a new GMM object. | |
| void | vl_gmm_reset (VlGMM *self) |
| Reset state. | |
| void | vl_gmm_set_covariance_lower_bound (VlGMM *self, double bound) |
| Set the lower bounds on diagonal covariance values. | |
| void | vl_gmm_set_covariance_lower_bounds (VlGMM *self, double const *bounds) |
| Set the lower bounds on diagonal covariance values. | |
| void | vl_gmm_set_initialization (VlGMM *self, VlGMMInitialization init) |
| Set initialization algorithm. | |
| void | vl_gmm_set_kmeans_init_object (VlGMM *self, VlKMeans *kmeans) |
| Set KMeans initialization object. | |
| void | vl_gmm_set_max_num_iterations (VlGMM *self, vl_size maxNumIterations) |
| Set maximum number of iterations. | |
| void | vl_gmm_set_num_repetitions (VlGMM *self, vl_size numRepetitions) |
| Set maximum number of repetitions. | |
| void | vl_gmm_set_verbosity (VlGMM *self, int verbosity) |
| Set verbosity level. | |
Get parameters | |
| vl_size | vl_gmm_get_num_repetitions (VlGMM const *self) |
| Get maximum number of repetitions. | |
Detailed Description
Gaussian Mixture Models - Implementation.
Definition in file gmm.c.
Define Documentation
| #define FLT VL_TYPE_FLOAT |
| #define FLT VL_TYPE_DOUBLE |
| #define VL_GMM_INSTANTIATING |
| #define VL_GMM_INSTANTIATING |
| #define VL_GMM_MIN_POSTERIOR 1e-2 |
| #define VL_GMM_MIN_PRIOR 1e-6 |
| #define VL_GMM_MIN_VARIANCE 1e-6 |
$
The density $p(|)$ induced on the training data is obtained by marginalizing the component selector $k$, obtaining \[ p(|) = {k=1}^{K} p( |,), p( |,) = {1}{{(2)^d}} [ -{1}{2} (-)^^{-1}(-) ]. \] Learning a GMM to fit a dataset $X=(, , )$ is usually done by maximizing the log-likelihood of the data:
![\[ \ell(\Theta;X) = E_{\bx\sim\hat p} [ \log p(\bx|\Theta) ] = \frac{1}{n}\sum_{i=1}^{n} \log \sum_{k=1}^{K} \pi_k p(\bx_i|\mu_k, \Sigma_k) \]](form_64.png)
where $ p$ is the empirical distribution of the data. An algorithm to solve this problem is introduced next.
Learning a GMM by expectation maximization
The direct maximization of the log-likelihood function of a GMM is difficult due to the fact that the assignments of points to Gaussian mode is not observable and, as such, must be treated as a latent variable.
Usually, GMMs are learned by using the *Expectation Maximization* (EM) algorithm [dempster77maximum]}. Consider in general the problem of estimating to the maximum likelihood a distribution $p(x|) = p(x,h|)\,dh$, where $x$ is a measurement, $h$ is a *latent variable*, and $$ are the model parameters. By introducing an auxiliary distribution $q(h|x)$ on the latent variable, one can use Jensen inequality to obtain the following lower bound on the log-likelihood:
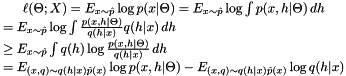
The first term of the last expression is the log-likelihood of the model where both the $x$ and $h$ are observed and joinlty distributed as $q(x|h) p(x)$; the second term is the a average entropy of the latent variable, which does not depend on $$. This lower bound is maximized and becomes tight by setting $q(h|x) = p(h|x,)$ to be the posterior distribution on the latent variable $h$ (given the current estimate of the parameters $$). In fact:
\[ E_{x p} p(x|) = E_{(x,h) p(h|x,) p(x)}[ {p(x,h|)}{p(h|x,)} ] = E_{(x,h) p(h|x,) p(x)} [ p(x|) ] = (;X). \]
EM alternates between updating the latent variable auxiliary distribution $q(h|x) = p(h|x,)$ (*expectation step*) given the current estimate of the parameters $$, and then updating the model parameters ${t+1}$ by maximizing the log-likelihood lower bound derived (*maximization step*). The simplification is that in the maximization step both $x$ and $h$ are now ``observed'' quantities. This procedure converges to a local optimum of the model log-likelihood.
Expectation step
In the case of a GMM, the latent variables are the point-to-cluster assignments $k_i, i=1,,n$, one for each of $n$ data points. The auxiliary distribution $q(k_i|) = q_{ik}$ is a matrix with $n K$ entries. Each row $q_{i,:}$ can be thought of as a vector of soft assignments of the data points $$ to each of the Gaussian modes. Setting $q_{ik} = p(k_i | , )$ yields
\[ q_{ik} = { p(|,)} {{l=1}^K p(|,)} \]
where the Gaussian density $p(|,)$ was given above.
One important point to keep in mind when these probabilities are computed is the fact that the Gaussian densities may attain very low values and underflow in a vanilla implementation. Furthermore, VLFeat GMM implementation restricts the covariance matrices to be diagonal. In this case, the computation of the determinant of $$ reduces to computing the trace of the matrix and the inversion of $$ could be obtained by inverting the elements on the diagonal of the covariance matrix.
Maximization step
The M step estimates the parameters of the Gaussian mixture components and the prior probabilities $$ given the auxiliary distribution on the point-to-cluster assignments computed in the E step. Since all the variables are now ``observed'', the estimate is quite simple. For example, the mean $$ of a Gaussian mode is obtained as the mean of the data points assigned to it (accounting for the strength of the soft assignments). The other quantities are obtained in a similar manner, yielding to:
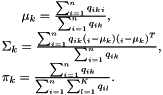
Initialization algorithms
The EM algorithm is a local optimization method. As such, the quality of the solution strongly depends on the quality of the initial values of the parameters (i.e. of the locations and shapes of the Gaussian modes).
gmm.h supports the following cluster initialization algorithms:
- Random data points. (vl_gmm_init_with_rand_data) This method sets the means of the modes by sampling at random a corresponding number of data points, sets the covariance matrices of all the modes are to the covariance of the entire dataset, and sets the prior probabilities of the Gaussian modes to be uniform. This initialization method is the fastest, simplest, as well as the one most likely to end in a bad local minimum.
- KMeans initialization (vl_gmm_init_with_kmeans) This method uses KMeans to pre-cluster the points. It then sets the means and covariances of the Gaussian distributions the sample means and covariances of each KMeans cluster. It also sets the prior probabilities to be proportional to the mass of each cluster. In order to use this initialization method, a user can specify an instance of VlKMeans by using the function vl_gmm_set_kmeans_init_object, or let VlGMM create one automatically.
Alternatively, one can manually specify a starting point (vl_gmm_set_priors, vl_gmm_set_means, vl_gmm_set_covariances).
| #define VL_SHUFFLE_prefix _vl_gmm |
| #define VL_SHUFFLE_type vl_uindex |
Function Documentation
| static void _vl_gmm_prepare_for_data | ( | VlGMM * | self, |
| vl_size | numData | ||
| ) | [static] |
| void vl_gmm_delete | ( | VlGMM * | self | ) |
Deletes a GMM object.
- Parameters:
-
self GMM object instance.
The function deletes the GMM object instance created by vl_gmm_new.
| double const* vl_gmm_get_covariance_lower_bounds | ( | VlGMM const * | self | ) |
| void const* vl_gmm_get_covariances | ( | VlGMM const * | self | ) |
| vl_type vl_gmm_get_data_type | ( | VlGMM const * | self | ) |
| vl_size vl_gmm_get_dimension | ( | VlGMM const * | self | ) |
| VlGMMInitialization vl_gmm_get_initialization | ( | VlGMM const * | self | ) |
| VlKMeans* vl_gmm_get_kmeans_init_object | ( | VlGMM const * | self | ) |
| double vl_gmm_get_loglikelihood | ( | VlGMM const * | self | ) |
| vl_size vl_gmm_get_max_num_iterations | ( | VlGMM const * | self | ) |
| void const* vl_gmm_get_means | ( | VlGMM const * | self | ) |
| vl_size vl_gmm_get_num_clusters | ( | VlGMM const * | self | ) |
| vl_size vl_gmm_get_num_data | ( | VlGMM const * | self | ) |
| VL_EXPORT vl_size vl_gmm_get_num_repetitions | ( | VlGMM const * | self | ) |
| void const* vl_gmm_get_posteriors | ( | VlGMM const * | self | ) |
| void const* vl_gmm_get_priors | ( | VlGMM const * | self | ) |
| int vl_gmm_get_verbosity | ( | VlGMM const * | self | ) |
| VlGMM* vl_gmm_new | ( | vl_type | dataType, |
| vl_size | dimension, | ||
| vl_size | numComponents | ||
| ) |
Create a new GMM object.
- Parameters:
-
dataType type of data (VL_TYPE_FLOAT or VL_TYPE_DOUBLE) dimension dimension of the data. numComponents number of Gaussian mixture components.
- Returns:
- new GMM object instance.
| void vl_gmm_reset | ( | VlGMM * | self | ) |
| void vl_gmm_set_covariance_lower_bound | ( | VlGMM * | self, |
| double | bound | ||
| ) |
Set the lower bounds on diagonal covariance values.
- Parameters:
-
self object. bound bound.
While there is one lower bound per dimension, this function sets all of them to the specified scalar. Use vl_gmm_set_covariance_lower_bounds to set them individually.
| void vl_gmm_set_covariance_lower_bounds | ( | VlGMM * | self, |
| double const * | bounds | ||
| ) |
Set the lower bounds on diagonal covariance values.
- Parameters:
-
self object. bounds bounds.
There is one lower bound per dimension. Use vl_gmm_set_covariance_lower_bound to set all of them to a given scalar.
| void vl_gmm_set_initialization | ( | VlGMM * | self, |
| VlGMMInitialization | init | ||
| ) |
| void vl_gmm_set_kmeans_init_object | ( | VlGMM * | self, |
| VlKMeans * | kmeans | ||
| ) |
| void vl_gmm_set_max_num_iterations | ( | VlGMM * | self, |
| vl_size | maxNumIterations | ||
| ) |
| void vl_gmm_set_num_repetitions | ( | VlGMM * | self, |
| vl_size | numRepetitions | ||
| ) |
| void vl_gmm_set_verbosity | ( | VlGMM * | self, |
| int | verbosity | ||
| ) |