Public Member Functions |
| returnValue | maximizeLagrangeTerm (const Expression &arg) |
| returnValue | maximizeMayerTerm (const Expression &arg) |
| returnValue | minimizeLagrangeTerm (const Expression &arg) |
| returnValue | minimizeMayerTerm (const Expression &arg) |
| returnValue | minimizeMayerTerm (const int &multiObjectiveIdx, const Expression &arg) |
| | OCP (const double &tStart_=0.0, const double &tEnd_=1.0, const int &N_=20) |
| | OCP (const double &tStart_, const double &tEnd_, const DVector &_numSteps) |
| | OCP (const double &tStart_, const Parameter &tEnd_, const int &N_=20) |
| | OCP (const Grid &grid_) |
| returnValue | subjectTo (const DifferentialEquation &differentialEquation_) |
| returnValue | subjectTo (const ConstraintComponent &component) |
| returnValue | subjectTo (int index_, const ConstraintComponent &component) |
| returnValue | subjectTo (const double lb_, const Expression &arg1, const Expression &arg2, const double ub_) |
| virtual | ~OCP () |
|
Adds a Least Square term of the form
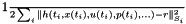
Here the sum is over all grid points of the objective grid. The DMatrix 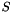 is assumed to be symmetric and positive (semi-) definite. The Function is assumed to be symmetric and positive (semi-) definite. The Function 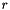 is called reference and can be specified by the user. The function is called reference and can be specified by the user. The function 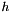 is a standard Function. is a standard Function.
- See also:
- Function
- Returns:
- SUCCESSFUL_RETURN
|
| returnValue | minimizeLSQ (const DMatrix &S, const Function &h, const DVector &r) |
| returnValue | minimizeLSQ (const Function &h, const DVector &r) |
| returnValue | minimizeLSQ (const Function &h) |
| returnValue | minimizeLSQ (const MatrixVariablesGrid &S, const Function &h, const VariablesGrid &r) |
| returnValue | minimizeLSQ (const DMatrix &S, const Function &h, const VariablesGrid &r) |
| returnValue | minimizeLSQ (const Function &h, const VariablesGrid &r) |
| returnValue | minimizeLSQ (const MatrixVariablesGrid &S, const Function &h, const char *rFilename) |
| returnValue | minimizeLSQ (const DMatrix &S, const Function &h, const char *rFilename) |
| returnValue | minimizeLSQ (const Function &h, const char *rFilename) |
| returnValue | minimizeLSQ (const DMatrix &S, const Function &h) |
| returnValue | minimizeLSQ (const BMatrix &S, const Function &h) |
| returnValue | minimizeLSQ (const DMatrix &S, const std::string &h) |
| returnValue | minimizeLSQ (const BMatrix &S, const std::string &h) |
|
|
| returnValue | minimizeLSQEndTerm (const DMatrix &S, const Function &m, const DVector &r) |
| returnValue | minimizeLSQEndTerm (const Function &m, const DVector &r) |
| returnValue | minimizeLSQEndTerm (const DMatrix &S, const Function &m) |
| returnValue | minimizeLSQEndTerm (const DMatrix &S, const std::string &m) |
| returnValue | minimizeLSQEndTerm (const BMatrix &S, const Function &m) |
| returnValue | minimizeLSQEndTerm (const BMatrix &S, const std::string &m) |
|
| returnValue | minimizeLSQLinearTerms (const DVector &Slx, const DVector &Slu) |
| returnValue | minimizeLSQLinearTerms (const BVector &Slx, const BVector &Slu) |
|
| returnValue | subjectTo (const double lb_, const Expression *arguments, const double ub_) |
|
Adds a constraint of the form
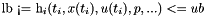
with constant lower and upper bounds.
|
| returnValue | subjectTo (const DVector &_lb, const Expression &_expr, const DVector &_ub) |
| returnValue | subjectTo (int _index, const DVector &_lb, const Expression &_expr, const DVector &_ub) |
|
| BooleanType | hasObjective () const |
| BooleanType | hasConstraint () const |
| returnValue | getGrid (Grid &grid_) const |
| returnValue | getObjective (Objective &objective_) const |
| returnValue | getObjective (const int &multiObjectiveIdx, Expression **arg) const |
| returnValue | getConstraint (Constraint &constraint_) const |
| returnValue | setObjective (const Objective &objective_) |
| returnValue | setConstraint (const Constraint &constraint_) |
| returnValue | setNumberIntegrationSteps (const uint numSteps) |
| virtual BooleanType | hasEquidistantGrid () const |
| double | getStartTime () const |
| double | getEndTime () const |
Protected Member Functions |
| void | setupGrid (double tStart, double tEnd, int N) |
| void | setupGrid (const DVector ×) |
Protected Attributes |
| std::tr1::shared_ptr< Constraint > | constraint |
| std::tr1::shared_ptr< Grid > | grid |
| std::tr1::shared_ptr< Objective > | objective |
Data class for defining optimal control problems.
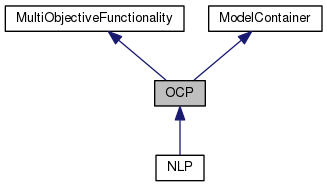
The class OCP is a data class for defining optimal control problems. In the most easiest an optimal control problem can consists of an objective only - i.e. in principle we can set up NLP's as well if no dynamic system is specified. However, in general the objective functional is optimized subject to a dynamic equation and different kind of constraints.
Note that the OCP class is only designed for the user and collects data only. In order to solve an OCP this class must be setup and passed to an appropriate OptimizationAlgorithm.
For setting up an optimal control problem (OCP), we should first specify the time horizon on which the OCP is defined. Note that there are several constructors available which allow to construct an OCP directly with the corresponding time interval. Here, the interval can consist of of given bounds, but in another variant a parameter can be passed in order to allow the setup of optimal control problems for which the end time is optimized, too.
Constraints can be specified with the "subjectTo" syntax. Please note that every parameter, state, control etc which is not fixed via a constraint will be regarded as an optimization variable. In particular, initial value or boundary constraints appear in many OCP formulations and of course all these constraints should all be set explicitly. Moreover, the dynamic equations (model) is regarded as a constraint, too.
Please note that the OCP class only collects the formulation of the problem. If initial values for non-linear problems should be specified, this needs to be done on the algorithm dealing with the OCP. (
- See also:
- OptimizationAlgorithm)
For advanced users and developers it might be important to know that the class OCP inherits the MultiObjectiveFunctionality which is needed if more than one objective should be specified.
Please check the tutorial examples as well as the class reference below, to learn about the usage of this class in more detail.
Definition at line 89 of file ocp.hpp.
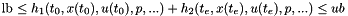
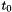 is the first and
is the first and 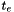 the last time point in the grid. Adds a constraint of the form
the last time point in the grid. Adds a constraint of the form 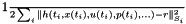
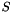 is assumed to be symmetric and positive (semi-) definite. The
is assumed to be symmetric and positive (semi-) definite. The 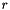 is called reference and can be specified by the user. The function
is called reference and can be specified by the user. The function 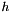 is a standard
is a standard 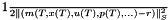
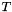 the time at the last objective grid point. The function
the time at the last objective grid point. The function 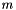 is a standard
is a standard