Standard Cholesky decomposition (LL^T) of a matrix and associated features. More...
#include <LLT.h>
Public Types | |
| enum | { RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime } |
| enum | { PacketSize = internal::packet_traits<Scalar>::size, AlignmentMask = int(PacketSize)-1, UpLo = _UpLo } |
| typedef MatrixType::Index | Index |
| typedef _MatrixType | MatrixType |
| typedef NumTraits< typename MatrixType::Scalar >::Real | RealScalar |
| typedef MatrixType::Scalar | Scalar |
| typedef internal::LLT_Traits < MatrixType, UpLo > | Traits |
Public Member Functions | |
| Index | cols () const |
| LLT & | compute (const MatrixType &matrix) |
| ComputationInfo | info () const |
| Reports whether previous computation was successful. | |
| LLT () | |
| Default Constructor. | |
| LLT (Index size) | |
| Default Constructor with memory preallocation. | |
| LLT (const MatrixType &matrix) | |
| Traits::MatrixL | matrixL () const |
| const MatrixType & | matrixLLT () const |
| Traits::MatrixU | matrixU () const |
| template<typename VectorType > | |
| LLT | rankUpdate (const VectorType &vec, const RealScalar &sigma=1) |
| MatrixType | reconstructedMatrix () const |
| Index | rows () const |
| template<typename Rhs > | |
| const internal::solve_retval < LLT, Rhs > | solve (const MatrixBase< Rhs > &b) const |
| template<typename Derived > | |
| void | solveInPlace (MatrixBase< Derived > &bAndX) const |
Static Protected Member Functions | |
| static void | check_template_parameters () |
Protected Attributes | |
| ComputationInfo | m_info |
| bool | m_isInitialized |
| MatrixType | m_matrix |
Detailed Description
template<typename _MatrixType, int _UpLo>
class Eigen::LLT< _MatrixType, _UpLo >
Standard Cholesky decomposition (LL^T) of a matrix and associated features.
- Parameters:
-
MatrixType the type of the matrix of which we are computing the LL^T Cholesky decomposition UpLo the triangular part that will be used for the decompositon: Lower (default) or Upper. The other triangular part won't be read.
This class performs a LL^T Cholesky decomposition of a symmetric, positive definite matrix A such that A = LL^* = U^*U, where L is lower triangular.
While the Cholesky decomposition is particularly useful to solve selfadjoint problems like D^*D x = b, for that purpose, we recommend the Cholesky decomposition without square root which is more stable and even faster. Nevertheless, this standard Cholesky decomposition remains useful in many other situations like generalised eigen problems with hermitian matrices.
Remember that Cholesky decompositions are not rank-revealing. This LLT decomposition is only stable on positive definite matrices, use LDLT instead for the semidefinite case. Also, do not use a Cholesky decomposition to determine whether a system of equations has a solution.
Example:
Output:
- See also:
- MatrixBase::llt(), class LDLT
Member Typedef Documentation
| typedef MatrixType::Index Eigen::LLT< _MatrixType, _UpLo >::Index |
| typedef _MatrixType Eigen::LLT< _MatrixType, _UpLo >::MatrixType |
| typedef NumTraits<typename MatrixType::Scalar>::Real Eigen::LLT< _MatrixType, _UpLo >::RealScalar |
| typedef MatrixType::Scalar Eigen::LLT< _MatrixType, _UpLo >::Scalar |
| typedef internal::LLT_Traits<MatrixType,UpLo> Eigen::LLT< _MatrixType, _UpLo >::Traits |
Member Enumeration Documentation
| anonymous enum |
| anonymous enum |
Constructor & Destructor Documentation
| Eigen::LLT< _MatrixType, _UpLo >::LLT | ( | ) | [inline] |
Default Constructor.
The default constructor is useful in cases in which the user intends to perform decompositions via LLT::compute(const MatrixType&).
| Eigen::LLT< _MatrixType, _UpLo >::LLT | ( | Index | size | ) | [inline] |
| Eigen::LLT< _MatrixType, _UpLo >::LLT | ( | const MatrixType & | matrix | ) | [inline] |
Member Function Documentation
| static void Eigen::LLT< _MatrixType, _UpLo >::check_template_parameters | ( | ) | [inline, static, protected] |
| Index Eigen::LLT< _MatrixType, _UpLo >::cols | ( | ) | const [inline] |
| LLT< MatrixType, _UpLo > & Eigen::LLT< MatrixType, _UpLo >::compute | ( | const MatrixType & | a | ) |
| ComputationInfo Eigen::LLT< _MatrixType, _UpLo >::info | ( | ) | const [inline] |
| Traits::MatrixL Eigen::LLT< _MatrixType, _UpLo >::matrixL | ( | ) | const [inline] |
| const MatrixType& Eigen::LLT< _MatrixType, _UpLo >::matrixLLT | ( | ) | const [inline] |
| Traits::MatrixU Eigen::LLT< _MatrixType, _UpLo >::matrixU | ( | ) | const [inline] |
| LLT< _MatrixType, _UpLo > Eigen::LLT< _MatrixType, _UpLo >::rankUpdate | ( | const VectorType & | v, |
| const RealScalar & | sigma = 1 |
||
| ) |
| MatrixType Eigen::LLT< MatrixType, _UpLo >::reconstructedMatrix | ( | ) | const |
| Index Eigen::LLT< _MatrixType, _UpLo >::rows | ( | ) | const [inline] |
| const internal::solve_retval<LLT, Rhs> Eigen::LLT< _MatrixType, _UpLo >::solve | ( | const MatrixBase< Rhs > & | b | ) | const [inline] |
- Returns:
- the solution x of
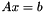using the current decomposition of A.
Since this LLT class assumes anyway that the matrix A is invertible, the solution theoretically exists and is unique regardless of b.
Example:
Output:
- See also:
- solveInPlace(), MatrixBase::llt()
| void Eigen::LLT< MatrixType, _UpLo >::solveInPlace | ( | MatrixBase< Derived > & | bAndX | ) | const |
Member Data Documentation
ComputationInfo Eigen::LLT< _MatrixType, _UpLo >::m_info [protected] |
bool Eigen::LLT< _MatrixType, _UpLo >::m_isInitialized [protected] |
MatrixType Eigen::LLT< _MatrixType, _UpLo >::m_matrix [protected] |
The documentation for this class was generated from the following file: