ACADO offers advanced and systematic features for efficiently solving optimal control problems with multiple and conflicting objectives. Typically, these Multi-Objective Optimal Control Problems (MOOCPs) give rise to a set of Pareto optimal solutions instead of one single optimum. This tutorial explains how to generate this Pareto set (or trade-off curve) efficiently.
Mathematical formulation of general Multi-Objective Optimal Control Problems
In contrast to the general optimal control problem formulation, in which only one objective has to be minimized, the general MOOCP formulation requires the simultaneous minimization of m objectives.
![\begin{eqnarray*} \displaystyle\min_{x(\cdot), u(\cdot), p, T} & {\Phi_1(x(\cdot), u(\cdot), p, T),\ldots,\Phi_j(x(\cdot), u(\cdot), p, T),\ldots,\Phi_m(x(\cdot), u(\cdot), p, T)} \\ \textrm{subject to} & \\ \forall t \in [0,T]: & 0 = F(t, x(t), \dot{x}(t), u(t), p), \\ \forall t \in [0,T]: & 0 \leq h(t, x(t), u(t), p), \\ & 0 = r(x(0), x(T), p)\\ \end{eqnarray*}](form_57.png)
Here, the function F still represents the model equation, with x the model states, u the control inputs, p the constant parameters, and T the final time. Now Φj denotes the j-th individual objective functional, while h and r are still the path constraints and boundary conditions of the optimal control problem.
Multi-Objective Optimization: concepts and philosophy
In contrast to the general optimal control problem formulation, in which only one objective has to be minimized, the general MOOCP formulation requires the simultaneous minimization of m objectives. Before continuing, some concepts of Multi-Objective Optimization and scalarization methods are briefly introduced.
- Pareto optimality concept. A feasible point is considered to be a solution to a multi-objective optimization problem, and is called Pareto optimal, when there exist no other feasible point that improves one of the objectives without worsening at least one of the other objectives. The set of these mathematically equivalent point is often referred to as the Pareto set or Pareto front. The figure above illustrates the Pareto concept for a bi-objective optimization problem. The feasible objective space is depicted in blue and the Pareto set is diplayed in green. Hence, all points a to e are Pareto optimal, while f and g are not.
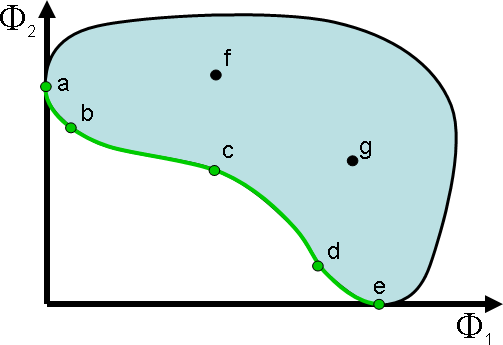 Pareto optimality concept
Pareto optimality concept
- Scalarization methods for multi-objective optimization problems. The rationale behind this class of solution methods is to convert the original multi-objective optimization problem into a series of parametric single objective optimization problems. By consistently varying the method's parameters an approximation of the Pareto front is obtained. Despite several intrinsic drawbacks, the convex Weighted Sum (WS) is still the most popular scalarization method. Alternatively, novel approaches that mitigate the drawbacks of the WS have been reported: Normal Boundary Intersection (NBI) and Normalized Normal Constraint (NNC).
Multi-objective implementation in ACADO Toolkit
The current structure and features of ACADO Multi-Objective are schematically depicted in the figure below. As multi-objective scalarization techniques WS, NNC and NBI are available. To provide an approximation of the Pareto, single objective optimization problems have to be solved for different sets of the scalarization method's reformulation parameters. These sets of parameters are automatically generated by the weights generation scheme. Hot-start re-initialization options allow to seed up the solution of this series of single objective optimization problems. Afterwards, whenever necessary, non-Pareto optimal solutions can be removed by the Pareto filter. Finally, the resulting Pareto set can be exported and visualized. However, visualization is limited to cases with up to three objectives.
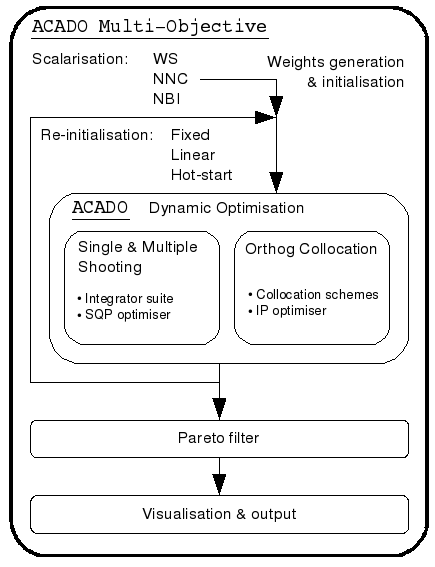
The following tutorials provide more detailed information on how to use ACADO Multi-Objective:
- Static Optimization Problem with Two Objectives Static nonlinear bi-objective optimization problem with non-convex Pareto front. Non-Pareto optimal points returned by NNC and NBI are removed by the Pareto filter.
- Static Optimization Problem with Three Objectives Static nonlinear tri-objective optimization problem.
- Optimal control of a plug flow reactor with conflicting energy and conversion objectives Dynamic bi-objective optimization problem
Next example: Static Optimization Problem with Two Objectives