Standard SVD decomposition of a matrix and associated features. More...
#include <SVD.h>
Public Member Functions | |
| void | compute (const MatrixType &matrix) |
| template<typename PositiveType , typename UnitaryType > | |
| void | computePositiveUnitary (PositiveType *positive, UnitaryType *unitary) const |
| template<typename UnitaryType , typename PositiveType > | |
| void | computePositiveUnitary (UnitaryType *positive, PositiveType *unitary) const |
| template<typename RotationType , typename ScalingType > | |
| void | computeRotationScaling (RotationType *unitary, ScalingType *positive) const |
| template<typename ScalingType , typename RotationType > | |
| void | computeScalingRotation (ScalingType *positive, RotationType *unitary) const |
| template<typename UnitaryType , typename PositiveType > | |
| void | computeUnitaryPositive (UnitaryType *unitary, PositiveType *positive) const |
| const MatrixUType & | matrixU () const |
| const MatrixVType & | matrixV () const |
| const SingularValuesType & | singularValues () const |
| template<typename OtherDerived , typename ResultType > | |
| bool | solve (const MatrixBase< OtherDerived > &b, ResultType *result) const |
| SVD & | sort () |
| SVD () | |
| SVD (const MatrixType &matrix) | |
Protected Attributes | |
| MatrixUType | m_matU |
| MatrixVType | m_matV |
| SingularValuesType | m_sigma |
Private Types | |
| enum | { PacketSize = internal::packet_traits<Scalar>::size, AlignmentMask = int(PacketSize)-1, MinSize = EIGEN_SIZE_MIN_PREFER_DYNAMIC(MatrixType::RowsAtCompileTime, MatrixType::ColsAtCompileTime) } |
| typedef Matrix< Scalar, MatrixType::RowsAtCompileTime, 1 > | ColVector |
| typedef Matrix< Scalar, MatrixType::RowsAtCompileTime, MinSize > | MatrixUType |
| typedef Matrix< Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime > | MatrixVType |
| typedef NumTraits< typename MatrixType::Scalar >::Real | RealScalar |
| typedef Matrix< Scalar, MatrixType::ColsAtCompileTime, 1 > | RowVector |
| typedef MatrixType::Scalar | Scalar |
| typedef Matrix< Scalar, MinSize, 1 > | SingularValuesType |
Detailed Description
template<typename MatrixType>
class Eigen::SVD< MatrixType >
Standard SVD decomposition of a matrix and associated features.
- Parameters:
-
MatrixType the type of the matrix of which we are computing the SVD decomposition
This class performs a standard SVD decomposition of a real matrix A of size M x N with M >= N.
- See also:
- MatrixBase::SVD()
Member Typedef Documentation
typedef Matrix<Scalar, MatrixType::RowsAtCompileTime, 1> Eigen::SVD< MatrixType >::ColVector [private] |
typedef Matrix<Scalar, MatrixType::RowsAtCompileTime, MinSize> Eigen::SVD< MatrixType >::MatrixUType [private] |
typedef Matrix<Scalar, MatrixType::ColsAtCompileTime, MatrixType::ColsAtCompileTime> Eigen::SVD< MatrixType >::MatrixVType [private] |
typedef NumTraits<typename MatrixType::Scalar>::Real Eigen::SVD< MatrixType >::RealScalar [private] |
typedef Matrix<Scalar, MatrixType::ColsAtCompileTime, 1> Eigen::SVD< MatrixType >::RowVector [private] |
typedef MatrixType::Scalar Eigen::SVD< MatrixType >::Scalar [private] |
typedef Matrix<Scalar, MinSize, 1> Eigen::SVD< MatrixType >::SingularValuesType [private] |
Member Enumeration Documentation
anonymous enum [private] |
Constructor & Destructor Documentation
| Eigen::SVD< MatrixType >::SVD | ( | ) | [inline] |
| Eigen::SVD< MatrixType >::SVD | ( | const MatrixType & | matrix | ) | [inline] |
Member Function Documentation
| void Eigen::SVD< MatrixType >::compute | ( | const MatrixType & | matrix | ) |
| void Eigen::SVD< MatrixType >::computePositiveUnitary | ( | PositiveType * | positive, |
| UnitaryType * | unitary | ||
| ) | const |
| void Eigen::SVD< MatrixType >::computePositiveUnitary | ( | UnitaryType * | positive, |
| PositiveType * | unitary | ||
| ) | const |
Computes the polar decomposition of the matrix, as a product positive x unitary.
If either pointer is zero, the corresponding computation is skipped.
Only for square matrices.
| void Eigen::SVD< MatrixType >::computeRotationScaling | ( | RotationType * | rotation, |
| ScalingType * | scaling | ||
| ) | const |
decomposes the matrix as a product rotation x scaling, the scaling being not necessarily positive.
If either pointer is zero, the corresponding computation is skipped.
This method requires the Geometry module.
| void Eigen::SVD< MatrixType >::computeScalingRotation | ( | ScalingType * | scaling, |
| RotationType * | rotation | ||
| ) | const |
decomposes the matrix as a product scaling x rotation, the scaling being not necessarily positive.
If either pointer is zero, the corresponding computation is skipped.
This method requires the Geometry module.
| void Eigen::SVD< MatrixType >::computeUnitaryPositive | ( | UnitaryType * | unitary, |
| PositiveType * | positive | ||
| ) | const |
Computes the polar decomposition of the matrix, as a product unitary x positive.
If either pointer is zero, the corresponding computation is skipped.
Only for square matrices.
| const MatrixUType& Eigen::SVD< MatrixType >::matrixU | ( | ) | const [inline] |
| const MatrixVType& Eigen::SVD< MatrixType >::matrixV | ( | ) | const [inline] |
| const SingularValuesType& Eigen::SVD< MatrixType >::singularValues | ( | ) | const [inline] |
| bool Eigen::SVD< MatrixType >::solve | ( | const MatrixBase< OtherDerived > & | b, |
| ResultType * | result | ||
| ) | const |
- Returns:
- the solution of
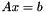 using the current SVD decomposition of A. The parts of the solution corresponding to zero singular values are ignored.
using the current SVD decomposition of A. The parts of the solution corresponding to zero singular values are ignored.
- See also:
- MatrixBase::svd(), LU::solve(), LLT::solve()
| SVD< MatrixType > & Eigen::SVD< MatrixType >::sort | ( | ) |
Member Data Documentation
MatrixUType Eigen::SVD< MatrixType >::m_matU [protected] |
MatrixVType Eigen::SVD< MatrixType >::m_matV [protected] |
SingularValuesType Eigen::SVD< MatrixType >::m_sigma [protected] |
The documentation for this class was generated from the following file: