Public Types | Public Member Functions | Static Public Attributes | Private Types | Private Member Functions | Private Attributes
Eigen::RealSchur< _MatrixType > Class Template Reference

Performs a real Schur decomposition of a square matrix. More...

#include <RealSchur.h>

List of all members.

Public Types

enum  {
  RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
  MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
}
typedef Matrix< Scalar,
ColsAtCompileTime, 1, Options
&~RowMajor,
MaxColsAtCompileTime, 1 > 		ColumnVectorType
typedef std::complex< typename
NumTraits< Scalar >::Real > 		ComplexScalar
typedef Matrix< ComplexScalar,
ColsAtCompileTime, 1, Options
&~RowMajor,
MaxColsAtCompileTime, 1 > 		EigenvalueType
typedef MatrixType::Index Index
typedef _MatrixType MatrixType
typedef MatrixType::Scalar Scalar

Public Member Functions

RealSchur & compute (const MatrixType &matrix, bool computeU=true)
 Computes Schur decomposition of given matrix.
template<typename HessMatrixType , typename OrthMatrixType >
RealSchur & computeFromHessenberg (const HessMatrixType &matrixH, const OrthMatrixType &matrixQ, bool computeU)
 Computes Schur decomposition of a Hessenberg matrix H = Z T Z^T.
Index getMaxIterations ()
 Returns the maximum number of iterations.
ComputationInfo info () const
 Reports whether previous computation was successful.
const MatrixType & matrixT () const
 Returns the quasi-triangular matrix in the Schur decomposition.
const MatrixType & matrixU () const
 Returns the orthogonal matrix in the Schur decomposition.
 RealSchur (Index size=RowsAtCompileTime==Dynamic?1:RowsAtCompileTime)
 Default constructor.
 RealSchur (const MatrixType &matrix, bool computeU=true)
 Constructor; computes real Schur decomposition of given matrix.
RealSchur & setMaxIterations (Index maxIters)
 Sets the maximum number of iterations allowed.

Static Public Attributes

static const int m_maxIterationsPerRow = 40
 Maximum number of iterations per row.

Private Types

typedef Matrix< Scalar, 3, 1 > Vector3s

Private Member Functions

Scalar computeNormOfT ()
void computeShift (Index iu, Index iter, Scalar &exshift, Vector3s &shiftInfo)
Index findSmallSubdiagEntry (Index iu, const Scalar &norm)
void initFrancisQRStep (Index il, Index iu, const Vector3s &shiftInfo, Index &im, Vector3s &firstHouseholderVector)
void performFrancisQRStep (Index il, Index im, Index iu, bool computeU, const Vector3s &firstHouseholderVector, Scalar *workspace)
void splitOffTwoRows (Index iu, bool computeU, const Scalar &exshift)

Private Attributes

HessenbergDecomposition
< MatrixType > 		m_hess
ComputationInfo m_info
bool m_isInitialized
MatrixType m_matT
MatrixType m_matU
bool m_matUisUptodate
Index m_maxIters
ColumnVectorType m_workspaceVector

Detailed Description

template<typename _MatrixType>
class Eigen::RealSchur< _MatrixType >

Performs a real Schur decomposition of a square matrix.

Template Parameters:
_MatrixTypethe type of the matrix of which we are computing the real Schur decomposition; this is expected to be an instantiation of the Matrix class template.

Given a real square matrix A, this class computes the real Schur decomposition: 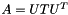$ A = U T U^T $ where U is a real orthogonal matrix and T is a real quasi-triangular matrix. An orthogonal matrix is a matrix whose inverse is equal to its transpose, 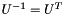$ U^{-1} = U^T $. A quasi-triangular matrix is a block-triangular matrix whose diagonal consists of 1-by-1 blocks and 2-by-2 blocks with complex eigenvalues. The eigenvalues of the blocks on the diagonal of T are the same as the eigenvalues of the matrix A, and thus the real Schur decomposition is used in EigenSolver to compute the eigendecomposition of a matrix.

Call the function compute() to compute the real Schur decomposition of a given matrix. Alternatively, you can use the RealSchur(const MatrixType&, bool) constructor which computes the real Schur decomposition at construction time. Once the decomposition is computed, you can use the matrixU() and matrixT() functions to retrieve the matrices U and T in the decomposition.

The documentation of RealSchur(const MatrixType&, bool) contains an example of the typical use of this class.

Note:
The implementation is adapted from JAMA (public domain). Their code is based on EISPACK.
See also:
class ComplexSchur, class EigenSolver, class ComplexEigenSolver

Definition at line 54 of file RealSchur.h.

Member Typedef Documentation

template<typename _MatrixType>
typedef Matrix<Scalar, ColsAtCompileTime, 1, Options & ~RowMajor, MaxColsAtCompileTime, 1> Eigen::RealSchur< _MatrixType >::ColumnVectorType

Definition at line 70 of file RealSchur.h.

template<typename _MatrixType>
typedef std::complex<typename NumTraits<Scalar>::Real> Eigen::RealSchur< _MatrixType >::ComplexScalar

Definition at line 66 of file RealSchur.h.

template<typename _MatrixType>
typedef Matrix<ComplexScalar, ColsAtCompileTime, 1, Options & ~RowMajor, MaxColsAtCompileTime, 1> Eigen::RealSchur< _MatrixType >::EigenvalueType

Definition at line 69 of file RealSchur.h.

template<typename _MatrixType>
typedef MatrixType::Index Eigen::RealSchur< _MatrixType >::Index

Definition at line 67 of file RealSchur.h.

template<typename _MatrixType>
typedef _MatrixType Eigen::RealSchur< _MatrixType >::MatrixType

Definition at line 57 of file RealSchur.h.

template<typename _MatrixType>
typedef MatrixType::Scalar Eigen::RealSchur< _MatrixType >::Scalar

Definition at line 65 of file RealSchur.h.

template<typename _MatrixType>
typedef Matrix<Scalar,3,1> Eigen::RealSchur< _MatrixType >::Vector3s [private]

Definition at line 234 of file RealSchur.h.

Member Enumeration Documentation

template<typename _MatrixType>
anonymous enum
Enumerator:
RowsAtCompileTime 
ColsAtCompileTime 
Options 
MaxRowsAtCompileTime 
MaxColsAtCompileTime 

Definition at line 58 of file RealSchur.h.

Constructor & Destructor Documentation

template<typename _MatrixType>
Eigen::RealSchur< _MatrixType >::RealSchur ( Index  size = RowsAtCompileTime==Dynamic ? 1 : RowsAtCompileTime) [inline]

Default constructor.

Parameters:
[in]sizePositive integer, size of the matrix whose Schur decomposition will be computed.

The default constructor is useful in cases in which the user intends to perform decompositions via compute(). The size parameter is only used as a hint. It is not an error to give a wrong size, but it may impair performance.

See also:
compute() for an example.

Definition at line 83 of file RealSchur.h.

template<typename _MatrixType>
Eigen::RealSchur< _MatrixType >::RealSchur ( const MatrixType &  matrix,
bool  computeU = true 
) [inline]

Constructor; computes real Schur decomposition of given matrix.

Parameters:
[in]matrixSquare matrix whose Schur decomposition is to be computed.
[in]computeUIf true, both T and U are computed; if false, only T is computed.

This constructor calls compute() to compute the Schur decomposition.

Example: 

 Output: 


 

Definition at line 103 of file RealSchur.h.







Member Function Documentation








template<typename MatrixType > 

      

        

          RealSchur< MatrixType > & Eigen::RealSchur< MatrixType >::compute 
          (
          const MatrixType & 
          matrix, 
        

        

          
          
          bool 
          computeU = true 
        

        

          
          )
          
        

      







Computes Schur decomposition of given matrix. 


Parameters:

  

    
[in]matrixSquare matrix whose Schur decomposition is to be computed. 

    
[in]computeUIf true, both T and U are computed; if false, only T is computed. 

  

  




Returns:
Reference to *this 


The Schur decomposition is computed by first reducing the matrix to Hessenberg form using the class HessenbergDecomposition. The Hessenberg matrix is then reduced to triangular form by performing Francis QR iterations with implicit double shift. The cost of computing the Schur decomposition depends on the number of iterations; as a rough guide, it may be taken to be 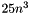$25n^3$ flops if computeU is true and 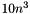$10n^3$ flops if computeU is false.


Example: 


 Output: 


See also:
compute(const MatrixType&, bool, Index) 



Definition at line 246 of file RealSchur.h.













template<typename MatrixType > 



template<typename HessMatrixType , typename OrthMatrixType > 

      

        

          RealSchur< MatrixType > & Eigen::RealSchur< MatrixType >::computeFromHessenberg 
          (
          const HessMatrixType & 
          matrixH, 
        

        

          
          
          const OrthMatrixType & 
          matrixQ, 
        

        

          
          
          bool 
          computeU 
        

        

          
          )
          
        

      







Computes Schur decomposition of a Hessenberg matrix H = Z T Z^T. 


Parameters:

  

    
[in]matrixHMatrix in Hessenberg form H 

    
[in]matrixQorthogonal matrix Q that transform a matrix A to H : A = Q H Q^T 

    
computeUComputes the matriX U of the Schur vectors 

  

  




Returns:
Reference to *this 


This routine assumes that the matrix is already reduced in Hessenberg form matrixH using either the class HessenbergDecomposition or another mean. It computes the upper quasi-triangular matrix T of the Schur decomposition of H When computeU is true, this routine computes the matrix U such that A = U T U^T = (QZ) T (QZ)^T = Q H Q^T where A is the initial matrix


NOTE Q is referenced if computeU is true; so, if the initial orthogonal matrix is not available, the user should give an identity matrix (Q.setIdentity())


See also:
compute(const MatrixType&, bool) 



Definition at line 263 of file RealSchur.h.













template<typename MatrixType > 

      

        

          MatrixType::Scalar Eigen::RealSchur< MatrixType >::computeNormOfT 
          (
          )
           [inline, private]
        

      







Definition at line 332 of file RealSchur.h.













template<typename MatrixType > 

      

        

          void Eigen::RealSchur< MatrixType >::computeShift 
          (
          Index 
          iu, 
        

        

          
          
          Index 
          iter, 
        

        

          
          
          Scalar & 
          exshift, 
        

        

          
          
          Vector3s & 
          shiftInfo 
        

        

          
          )
           [inline, private]
        

      







Definition at line 399 of file RealSchur.h.













template<typename MatrixType > 

      

        

          MatrixType::Index Eigen::RealSchur< MatrixType >::findSmallSubdiagEntry 
          (
          Index 
          iu, 
        

        

          
          
          const Scalar & 
          norm 
        

        

          
          )
           [inline, private]
        

      







Definition at line 346 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          Index Eigen::RealSchur< _MatrixType >::getMaxIterations 
          (
          )
           [inline]
        

      







Returns the maximum number of iterations. 



Definition at line 211 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          ComputationInfo Eigen::RealSchur< _MatrixType >::info 
          (
          )
           const [inline]
        

      







Reports whether previous computation was successful. 


Returns:
Success if computation was succesful, NoConvergence otherwise. 



Definition at line 193 of file RealSchur.h.













template<typename MatrixType > 

      

        

          void Eigen::RealSchur< MatrixType >::initFrancisQRStep 
          (
          Index 
          il, 
        

        

          
          
          Index 
          iu, 
        

        

          
          
          const Vector3s & 
          shiftInfo, 
        

        

          
          
          Index & 
          im, 
        

        

          
          
          Vector3s & 
          firstHouseholderVector 
        

        

          
          )
           [inline, private]
        

      







Definition at line 441 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          const MatrixType& Eigen::RealSchur< _MatrixType >::matrixT 
          (
          )
           const [inline]
        

      







Returns the quasi-triangular matrix in the Schur decomposition. 


Returns:
A const reference to the matrix T.


Precondition:
Either the constructor RealSchur(const MatrixType&, bool) or the member function compute(const MatrixType&, bool) has been called before to compute the Schur decomposition of a matrix.


See also:
RealSchur(const MatrixType&, bool) for an example 



Definition at line 143 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          const MatrixType& Eigen::RealSchur< _MatrixType >::matrixU 
          (
          )
           const [inline]
        

      







Returns the orthogonal matrix in the Schur decomposition. 


Returns:
A const reference to the matrix U.


Precondition:
Either the constructor RealSchur(const MatrixType&, bool) or the member function compute(const MatrixType&, bool) has been called before to compute the Schur decomposition of a matrix, and computeU was set to true (the default value).


See also:
RealSchur(const MatrixType&, bool) for an example 



Definition at line 126 of file RealSchur.h.













template<typename MatrixType > 

      

        

          void Eigen::RealSchur< MatrixType >::performFrancisQRStep 
          (
          Index 
          il, 
        

        

          
          
          Index 
          im, 
        

        

          
          
          Index 
          iu, 
        

        

          
          
          bool 
          computeU, 
        

        

          
          
          const Vector3s & 
          firstHouseholderVector, 
        

        

          
          
          Scalar * 
          workspace 
        

        

          
          )
           [inline, private]
        

      







Definition at line 468 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          RealSchur& Eigen::RealSchur< _MatrixType >::setMaxIterations 
          (
          Index 
          maxIters)
           [inline]
        

      







Sets the maximum number of iterations allowed. 


If not specified by the user, the maximum number of iterations is m_maxIterationsPerRow times the size of the matrix. 



Definition at line 204 of file RealSchur.h.













template<typename MatrixType > 

      

        

          void Eigen::RealSchur< MatrixType >::splitOffTwoRows 
          (
          Index 
          iu, 
        

        

          
          
          bool 
          computeU, 
        

        

          
          
          const Scalar & 
          exshift 
        

        

          
          )
           [inline, private]
        

      







Definition at line 364 of file RealSchur.h.







Member Data Documentation








template<typename _MatrixType> 

      

        

          HessenbergDecomposition<MatrixType> Eigen::RealSchur< _MatrixType >::m_hess [private]
        

      







Definition at line 228 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          ComputationInfo Eigen::RealSchur< _MatrixType >::m_info [private]
        

      







Definition at line 229 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          bool Eigen::RealSchur< _MatrixType >::m_isInitialized [private]
        

      







Definition at line 230 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          MatrixType Eigen::RealSchur< _MatrixType >::m_matT [private]
        

      







Definition at line 225 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          MatrixType Eigen::RealSchur< _MatrixType >::m_matU [private]
        

      







Definition at line 226 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          bool Eigen::RealSchur< _MatrixType >::m_matUisUptodate [private]
        

      







Definition at line 231 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          const int Eigen::RealSchur< _MatrixType >::m_maxIterationsPerRow = 40 [static]
        

      







Maximum number of iterations per row. 


If not otherwise specified, the maximum number of iterations is this number times the size of the matrix. It is currently set to 40. 



Definition at line 221 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          Index Eigen::RealSchur< _MatrixType >::m_maxIters [private]
        

      







Definition at line 232 of file RealSchur.h.













template<typename _MatrixType> 

      

        

          ColumnVectorType Eigen::RealSchur< _MatrixType >::m_workspaceVector [private]
        

      







Definition at line 227 of file RealSchur.h.







The documentation for this class was generated from the following file:







acado

Author(s): Milan Vukov, Rien Quirynen

autogenerated on Sat Jun 8 2019 19:40:52