Function optimization

Classes
struct	TooN::ConjugateGradient< Size, Precision >
class	TooN::DownhillSimplex< N, Precision >
struct	TooN::Internal::LineSearch< Size, Precision, Func >
Functions
template<typename Precision , typename Func >
Matrix< 3, 2, Precision >	TooN::Internal::bracket_minimum_forward (Precision a_val, const Func &func, Precision initial_lambda, Precision zeps)
template<class Functor , class Precision >
Vector< 2, Precision >	TooN::brent_line_search (Precision a, Precision x, Precision b, Precision fx, const Functor &func, int maxiterations, Precision tolerance=sqrt(numeric_limits< Precision >::epsilon()), Precision epsilon=numeric_limits< Precision >::epsilon())
template<class Functor , class Precision >
Vector< 2, Precision >	TooN::golden_section_search (Precision a, Precision b, Precision c, const Functor &func, int maxiterations, Precision tol=sqrt(numeric_limits< Precision >::epsilon()))
template<class Functor , class Precision >
Vector< 2, Precision >	TooN::golden_section_search (Precision a, Precision b, Precision c, Precision fb, const Functor &func, int maxiterations, Precision tol=sqrt(numeric_limits< Precision >::epsilon()))

---

Detailed Description

Classes and functions to perform function optimization.

One dimensional function optimization

The following functions find the minimum of a 1-D function:

• golden_section_search()
• brent_line_search()

Multidimensional dimensional function optimization

The following classes perform multidimensional function minimization:

• TooN::DownhillSimplex
• TooN::ConjugateGradient

The mode of operation is to set up a mutable class, then repeatedly call an iterate function. This allows different sub algorithms (such as termination conditions) to be substituted in if need be.

---

Function Documentation

template<typename Precision , typename Func >

Matrix<3,2,Precision> TooN::Internal::bracket_minimum_forward	(	Precision	a_val,
		const Func &	func,
		Precision	initial_lambda,
		Precision	zeps
	)			[inline]

Bracket a 1D function by searching forward from zero. The assumption is that a minima exists in 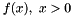, and this function searches for a bracket using exponentially growning or shrinking steps.

Parameters:

	a_val	The value of the function at zero.
	func	Function to bracket
	initial_lambda	Initial stepsize
	zeps	Minimum bracket size.

Returns:

m[i][0] contains the values of 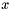for the bracket, in increasing order, and m[i][1] contains the corresponding values of 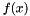. If the bracket drops below the minimum bracket size, all zeros are returned.

Definition at line 45 of file conjugate_gradient.h.

template<class Functor , class Precision >

Vector<2, Precision> TooN::brent_line_search	(	Precision	a,
		Precision	x,
		Precision	b,
		Precision	fx,
		const Functor &	func,
		int	maxiterations,
		Precision	tolerance = sqrt(numeric_limits<Precision>::epsilon()),
		Precision	epsilon = numeric_limits<Precision>::epsilon()
	)			[inline]

brent_line_search performs Brent's golden section/quadratic interpolation search on the functor provided. The inputs a, x, b must bracket the minimum, and must be in order, so that 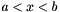and .

Parameters:

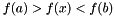	a	The most negative point along the line.
	x	The central point.
	fx	The value of the function at the central point ().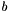
	b	The most positive point along the line.
	func	The functor to minimize
	maxiterations	Maximum number of iterations
	tolerance	Tolerance at which the search should be stopped (defults to sqrt machine precision)
	epsilon	Minimum bracket width (defaults to machine precision)

Returns:

The minima position is returned as the first element of the vector, and the minimal value as the second element.

Definition at line 29 of file brent.h.

template<class Functor , class Precision >

Vector<2, Precision> TooN::golden_section_search	(	Precision	a,
		Precision	b,
		Precision	c,
		const Functor &	func,
		int	maxiterations,
		Precision	tol = sqrt(numeric_limits<Precision>::epsilon())
	)			[inline]

golden_section_search performs a golden section search line minimization on the functor provided. The inputs a, b, c must bracket the minimum, and must be in order, so that 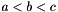and .

Parameters:

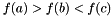	a	The most negative point along the line.
	b	The central point.
	c	The most positive point along the line.
	func	The functor to minimize
	maxiterations	Maximum number of iterations
	tol	Tolerance at which the search should be stopped.

Returns:

The minima position is returned as the first element of the vector, and the minimal value as the second element.

Definition at line 105 of file golden_section.h.

template<class Functor , class Precision >

Vector<2, Precision> TooN::golden_section_search	(	Precision	a,
		Precision	b,
		Precision	c,
		Precision	fb,
		const Functor &	func,
		int	maxiterations,
		Precision	tol = sqrt(numeric_limits<Precision>::epsilon())
	)			[inline]

golden_section_search performs a golden section search line minimization on the functor provided. The inputs a, b, c must bracket the minimum, and must be in order, so that 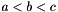and .

Parameters:

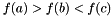	a	The most negative point along the line.
	b	The central point.
	fb	The value of the function at the central point ().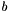
	c	The most positive point along the line.
	func	The functor to minimize
	maxiterations	Maximum number of iterations
	tol	Tolerance at which the search should be stopped.

Returns:

The minima position is returned as the first element of the vector, and the minimal value as the second element.

Definition at line 26 of file golden_section.h.