TooN::DownhillSimplex< N, Precision > Class Template Reference
[Function optimization]

#include <downhill_simplex.h>

Public Member Functions
template<class Function >
	DownhillSimplex (const Function &func, const Vector< N > &c, Precision spread=1)
template<class Function >
void	find_next_point (const Function &func)
bool	finished ()
int	get_best () const
	Get the index of the best vertex.
const Simplex &	get_simplex () const
	Return the simplex.
const Values &	get_values () const
	Return the score at the vertices.
int	get_worst () const
	Get the index of the worst vertex.
template<class Function >
bool	iterate (const Function &func)
template<class Function >
void	restart (const Function &func, Precision spread)
template<class Function >
void	restart (const Function &func, const Vector< N > &c, Precision spread)
Public Attributes
Precision	alpha
	Reflected size. Defaults to 1.
Precision	epsilon
	Tolerance used to determine if the optimization is complete. Defaults to square root of machine precision.
Precision	gamma
	Contraction ratio. Defaults to .5.
Precision	rho
	Expansion ratio. Defaults to 2.
Precision	sigma
	Shrink ratio. Defaults to .5.
Precision	zero_epsilon
	Additive term in tolerance to prevent excessive iterations if 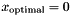$x_\mathrm{optimal} = 0$ . Known as `ZEPS` in numerical recipies. Defaults to 1e-20.
Private Types
typedef Matrix< Vertices, N, Precision >	Simplex
typedef Vector< Vertices, Precision >	Values
Private Attributes
Simplex	simplex
Values	values
Static Private Attributes
static const int	Vertices = (N==-1?-1:N+1)

Detailed Description

template<int N = -1, typename Precision = double>
class TooN::DownhillSimplex< N, Precision >

This is an implementation of the Downhill Simplex (Nelder & Mead, 1965) algorithm. This particular instance will minimize a given function.

The function maintains 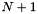$N+1$ points for a $N$ dimensional function,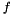 $f$

At each iteration, the following algorithm is performed:

Find the worst (largest) point, .
Find the centroid of the remaining points, .
Let
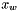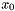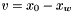
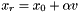
Compute a reflected point, $x_r = x_0 + \alpha v$
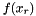If is better than the best point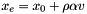
- Expand the simplex by extending the reflection to $x_e = x_0 + \rho \alpha v$
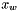- Replace with the best point of 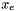, and .
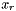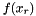Else, if is between the best and second-worst point
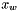- Replace with .
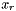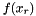Else, if is better than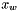
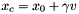
- Contract the simplex by computing $x_c = x_0 + \gamma v$
- If
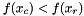
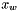  - Replace with .
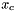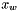If has not been replaced, then shrink the simplex by a factor of 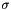$\sigma$ around the best point.

This implementation uses:

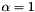
$\alpha = 1$
$\rho = 2$
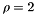
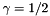
$\gamma = 1/2$
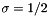
$\sigma = 1/2$

Example usage:

#include <TooN/optimization/downhill_simplex.h>
using namespace std;
using namespace TooN;

double sq(double x)
{
        return x*x;
}

double Rosenbrock(const Vector<2>& v)
{
                return sq(1 - v[0]) + 100 * sq(v[1] - sq(v[0]));
}

int main()
{
                Vector<2> starting_point = makeVector( -1, 1);

                DownhillSimplex<2> dh_fixed(Rosenbrock, starting_point, 1);

                while(dh_fixed.iterate(Rosenbrock))
                {
                        cout << dh.get_values()[dh.get_best()] << endl;
                }
                
                cout << dh_fixed.get_simplex()[dh_fixed.get_best()] << endl;
}

Parameters:

N

The dimension of the function to optimize. As usual, the default value of N (-1) indicates that the class is sized at run-time.

Definition at line 77 of file downhill_simplex.h.

Member Typedef Documentation

template<int N = -1, typename Precision = double>

typedef Matrix<Vertices, N, Precision> TooN::DownhillSimplex< N, Precision >::Simplex [private]

Definition at line 80 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

typedef Vector<Vertices, Precision> TooN::DownhillSimplex< N, Precision >::Values [private]

Definition at line 81 of file downhill_simplex.h.

Constructor & Destructor Documentation

template<int N = -1, typename Precision = double>

template<class Function >

TooN::DownhillSimplex< N, Precision >::DownhillSimplex	(	const Function &	func,
		const Vector< N > &	c,
		Precision	spread = `1`
	)			`[inline]`

Initialize the DownhillSimplex class. The simplex is automatically generated. One point is at c, the remaining points are made by moving c by spread along each axis aligned unit vector.

Parameters:

	func	Functor to minimize.
	c	Origin of the initial simplex. The dimension of this vector is used to determine the dimension of the run-time sized version.
	spread	Size of the initial simplex.

Definition at line 92 of file downhill_simplex.h.

Member Function Documentation

template<int N = -1, typename Precision = double>

template<class Function >

void TooN::DownhillSimplex< N, Precision >::find_next_point ( const Function & func ) [inline]

Perform one iteration of the downhill Simplex algorithm

Parameters:

func

Functor to minimize

Definition at line 175 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

bool TooN::DownhillSimplex< N, Precision >::finished ( ) [inline]

Check to see it iteration should stop. You probably do not want to use this function. See iterate() instead. This function updates nothing. The termination criterion is that the simplex span (distancve between the best and worst vertices) is small compared to the scale or small overall.

Definition at line 129 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

int TooN::DownhillSimplex< N, Precision >::get_best ( ) const [inline]

Get the index of the best vertex.

Definition at line 162 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

const Simplex& TooN::DownhillSimplex< N, Precision >::get_simplex ( ) const [inline]

Return the simplex.

Definition at line 150 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

const Values& TooN::DownhillSimplex< N, Precision >::get_values ( ) const [inline]

Return the score at the vertices.

Definition at line 156 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

int TooN::DownhillSimplex< N, Precision >::get_worst ( ) const [inline]

Get the index of the worst vertex.

Definition at line 168 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

template<class Function >

bool TooN::DownhillSimplex< N, Precision >::iterate ( const Function & func ) [inline]

Perform one iteration of the downhill Simplex algorithm, and return the result of not DownhillSimplex::finished.

Parameters:

func

Functor to minimize

Definition at line 273 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

template<class Function >

void TooN::DownhillSimplex< N, Precision >::restart	(	const Function &	func,
		Precision	spread
	)			`[inline]`

This function resets the simplex around the best current point.

Parameters:

	func	Functor to minimize.
	spread	simplex size

Definition at line 144 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

template<class Function >

void TooN::DownhillSimplex< N, Precision >::restart	(	const Function &	func,
		const Vector< N > &	c,
		Precision	spread
	)			`[inline]`

This function sets up the simplex around, with one point at c and the remaining points are made by moving by spread along each axis aligned unit vector.

Parameters:

	func	Functor to minimize.
	c	c corner point of the simplex
	spread	spread simplex size

Definition at line 112 of file downhill_simplex.h.

Member Data Documentation

template<int N = -1, typename Precision = double>

Precision TooN::DownhillSimplex< N, Precision >::alpha

Reflected size. Defaults to 1.

Definition at line 279 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

Precision TooN::DownhillSimplex< N, Precision >::epsilon

Tolerance used to determine if the optimization is complete. Defaults to square root of machine precision.

Definition at line 283 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

Precision TooN::DownhillSimplex< N, Precision >::gamma

Contraction ratio. Defaults to .5.

Definition at line 281 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

Precision TooN::DownhillSimplex< N, Precision >::rho

Expansion ratio. Defaults to 2.

Definition at line 280 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

Precision TooN::DownhillSimplex< N, Precision >::sigma

Shrink ratio. Defaults to .5.

Definition at line 282 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

Simplex TooN::DownhillSimplex< N, Precision >::simplex [private]

Definition at line 289 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

Values TooN::DownhillSimplex< N, Precision >::values [private]

Definition at line 292 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

const int TooN::DownhillSimplex< N, Precision >::Vertices = (N==-1?-1:N+1) [static, private]

Definition at line 79 of file downhill_simplex.h.

template<int N = -1, typename Precision = double>

Precision TooN::DownhillSimplex< N, Precision >::zero_epsilon

Additive term in tolerance to prevent excessive iterations if 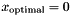$x_\mathrm{optimal} = 0$ . Known as ZEPS in numerical recipies. Defaults to 1e-20.

Definition at line 284 of file downhill_simplex.h.

The documentation for this class was generated from the following file:

downhill_simplex.h

TooN::DownhillSimplex< N, Precision > Class Template Reference [Function optimization]

Public Member Functions

Public Attributes

Private Types

Private Attributes

Static Private Attributes

Detailed Description

template<int N = -1, typename Precision = double> class TooN::DownhillSimplex< N, Precision >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

TooN::DownhillSimplex< N, Precision > Class Template Reference
[Function optimization]

template<int N = -1, typename Precision = double>
class TooN::DownhillSimplex< N, Precision >