TooN::ConjugateGradient< Size, Precision > Struct Template Reference
[Function optimization]

#include <conjugate_gradient.h>

List of all members.

Public Member Functions

template<class Func >
 ConjugateGradient (const Vector< Size > &start, const Func &func, const Vector< Size > &deriv)
template<class Func , class Deriv >
 ConjugateGradient (const Vector< Size > &start, const Func &func, const Deriv &deriv)
template<class Func >
void find_next_point (const Func &func)
bool finished ()
void init (const Vector< Size > &start, const Precision &func, const Vector< Size > &deriv)
template<class Func , class Deriv >
bool iterate (const Func &func, const Deriv &deriv)
void update_vectors_PR (const Vector< Size > &grad)

Public Attributes

Precision bracket_epsilon
 Minimum size for initial minima bracketing. Below this, it is assumed that the system has converged. Defaults to 1e-20.
Precision bracket_initial_lambda
 Initial stepsize used in bracketing the minimum for the line search. Defaults to 1.
Precision epsilon
 Additive term in tolerance to prevent excessive iterations if 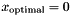$x_\mathrm{optimal} = 0$. Known as ZEPS in numerical recipies. Defaults to 1e-20.
Vector< Size > g
 Gradient vector used by the next call to iterate().
Vector< Size > h
 Conjugate vector to be searched along in the next call to iterate().
int iterations
 Number of iterations performed.
Precision linesearch_epsilon
 Additive term in tolerance to prevent excessive iterations if 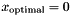$x_\mathrm{optimal} = 0$. Known as ZEPS in numerical recipies. Defaults to 1e-20.
int linesearch_max_iterations
 Maximum number of iterations in the linesearch. Defaults to 100.
Precision linesearch_tolerance
 Tolerance used to determine if the linesearch is complete. Defaults to square root of machine precision.
int max_iterations
 Maximum number of iterations. Defaults to size$*100$.
Vector< Size > minus_h
 negative of h as this is required to be passed into a function which uses references (so can't be temporary)
Vector< Size > old_g
 Gradient vector used to compute $h$ in the last call to iterate().
Vector< Size > old_h
 Conjugate vector searched along in the last call to iterate().
Vector< Size > old_x
 Previous best known point (not set at construction).
Precision old_y
 Function at old_x.
const int size
 Dimensionality of the space.
Precision tolerance
 Tolerance used to determine if the optimization is complete. Defaults to square root of machine precision.
Vector< Size > x
 Current position (best known point).
Precision y
 Function at 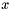$x$.

Detailed Description

template<int Size, class Precision = double>
struct TooN::ConjugateGradient< Size, Precision >

This class provides a nonlinear conjugate-gradient optimizer. The following code snippet will perform an optimization on the Rosenbrock Bananna function in two dimensions:

double Rosenbrock(const Vector<2>& v)
{
                return sq(1 - v[0]) + 100 * sq(v[1] - sq(v[0]));
}

Vector<2> RosenbrockDerivatives(const Vector<2>& v)
{
        double x = v[0];
        double y = v[1];

        Vector<2> ret;
        ret[0] = -2+2*x-400*(y-sq(x))*x;
        ret[1] = 200*y-200*sq(x);

        return ret;
}

int main()
{
        ConjugateGradient<2> cg(makeVector(0,0), Rosenbrock, RosenbrockDerivatives);

        while(cg.iterate(Rosenbrock, RosenbrockDerivatives))
                cout << "y_" << iteration << " = " << cg.y << endl;

        cout << "Optimal value: " << cg.y << endl;
}

The chances are that you will want to read the documentation for ConjugateGradient::ConjugateGradient and ConjugateGradient::iterate.

Linesearch is currently performed using golden-section search and conjugate vector updates are performed using the Polak-Ribiere equations. There many tunable parameters, and the internals are readily accessible, so alternative termination conditions etc can easily be substituted. However, ususally these will not be necessary.

Definition at line 195 of file conjugate_gradient.h.

Constructor & Destructor Documentation

template<int Size, class Precision = double>
template<class Func , class Deriv >
TooN::ConjugateGradient< Size, Precision >::ConjugateGradient ( const Vector< Size > &  start,
const Func &  func,
const Deriv &  deriv 
) [inline]

Initialize the ConjugateGradient class with sensible values.

Parameters:
start Starting point, x
func Function f to compute 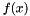$f(x)$
deriv Function to compute 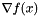$\nabla f(x)$

Definition at line 225 of file conjugate_gradient.h.

template<int Size, class Precision = double>
template<class Func >
TooN::ConjugateGradient< Size, Precision >::ConjugateGradient ( const Vector< Size > &  start,
const Func &  func,
const Vector< Size > &  deriv 
) [inline]

Initialize the ConjugateGradient class with sensible values.

Parameters:
start Starting point, x
func Function f to compute 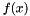$f(x)$
deriv 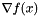$\nabla f(x)$

Definition at line 236 of file conjugate_gradient.h.

Member Function Documentation

template<int Size, class Precision = double>
template<class Func >
void TooN::ConjugateGradient< Size, Precision >::find_next_point ( const Func &  func  )  [inline]

Perform a linesearch from the current point (x) along the current conjugate vector (h). The linesearch does not make use of derivatives. You probably do not want to use this function. See iterate() instead. This function updates:

  • x
  • old_c
  • y
  • old_y
  • iterations Note that the conjugate direction and gradient are not updated. If bracket_minimum_forward detects a local maximum, then essentially a zero sized step is taken.
    Parameters:
    func Functor returning the function value at a given point.

Definition at line 291 of file conjugate_gradient.h.

template<int Size, class Precision = double>
bool TooN::ConjugateGradient< Size, Precision >::finished (  )  [inline]

Check to see it iteration should stop. You probably do not want to use this function. See iterate() instead. This function updates nothing.

Definition at line 344 of file conjugate_gradient.h.

template<int Size, class Precision = double>
void TooN::ConjugateGradient< Size, Precision >::init ( const Vector< Size > &  start,
const Precision &  func,
const Vector< Size > &  deriv 
) [inline]

Initialize the ConjugateGradient class with sensible values. Used internally.

Parameters:
start Starting point, x
func 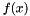$f(x)$
deriv 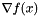$\nabla f(x)$

Definition at line 247 of file conjugate_gradient.h.

template<int Size, class Precision = double>
template<class Func , class Deriv >
bool TooN::ConjugateGradient< Size, Precision >::iterate ( const Func &  func,
const Deriv &  deriv 
) [inline]

Use this function to iterate over the optimization. Note that after iterate returns false, g, h, old_g and old_h will not have been updated. This function updates:

  • x
  • old_c
  • y
  • old_y
  • iterations
  • g*
  • old_g*
  • h*
  • old_h* 'd variables not updated on the last iteration.
    Parameters:
    func Functor returning the function value at a given point.
    deriv Functor to compute derivatives at the specified point.
    Returns:
    Whether to continue.

Definition at line 388 of file conjugate_gradient.h.

template<int Size, class Precision = double>
void TooN::ConjugateGradient< Size, Precision >::update_vectors_PR ( const Vector< Size > &  grad  )  [inline]

After an iteration, update the gradient and conjugate using the Polak-Ribiere equations. This function updates:

  • g
  • old_g
  • h
  • old_h
    Parameters:
    grad The derivatives of the function at x

Definition at line 358 of file conjugate_gradient.h.

Member Data Documentation

template<int Size, class Precision = double>
Precision TooN::ConjugateGradient< Size, Precision >::bracket_epsilon

Minimum size for initial minima bracketing. Below this, it is assumed that the system has converged. Defaults to 1e-20.

Definition at line 217 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Precision TooN::ConjugateGradient< Size, Precision >::bracket_initial_lambda

Initial stepsize used in bracketing the minimum for the line search. Defaults to 1.

Definition at line 212 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Precision TooN::ConjugateGradient< Size, Precision >::epsilon

Additive term in tolerance to prevent excessive iterations if 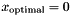$x_\mathrm{optimal} = 0$. Known as ZEPS in numerical recipies. Defaults to 1e-20.

Definition at line 209 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Vector<Size> TooN::ConjugateGradient< Size, Precision >::g

Gradient vector used by the next call to iterate().

Definition at line 198 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Vector<Size> TooN::ConjugateGradient< Size, Precision >::h

Conjugate vector to be searched along in the next call to iterate().

Definition at line 199 of file conjugate_gradient.h.

template<int Size, class Precision = double>
int TooN::ConjugateGradient< Size, Precision >::iterations

Number of iterations performed.

Definition at line 219 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Precision TooN::ConjugateGradient< Size, Precision >::linesearch_epsilon

Additive term in tolerance to prevent excessive iterations if 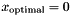$x_\mathrm{optimal} = 0$. Known as ZEPS in numerical recipies. Defaults to 1e-20.

Definition at line 214 of file conjugate_gradient.h.

template<int Size, class Precision = double>
int TooN::ConjugateGradient< Size, Precision >::linesearch_max_iterations

Maximum number of iterations in the linesearch. Defaults to 100.

Definition at line 215 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Precision TooN::ConjugateGradient< Size, Precision >::linesearch_tolerance

Tolerance used to determine if the linesearch is complete. Defaults to square root of machine precision.

Definition at line 213 of file conjugate_gradient.h.

template<int Size, class Precision = double>
int TooN::ConjugateGradient< Size, Precision >::max_iterations

Maximum number of iterations. Defaults to size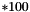$*100$.

Definition at line 210 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Vector<Size> TooN::ConjugateGradient< Size, Precision >::minus_h

negative of h as this is required to be passed into a function which uses references (so can't be temporary)

Definition at line 200 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Vector<Size> TooN::ConjugateGradient< Size, Precision >::old_g

Gradient vector used to compute $h$ in the last call to iterate().

Definition at line 201 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Vector<Size> TooN::ConjugateGradient< Size, Precision >::old_h

Conjugate vector searched along in the last call to iterate().

Definition at line 202 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Vector<Size> TooN::ConjugateGradient< Size, Precision >::old_x

Previous best known point (not set at construction).

Definition at line 204 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Precision TooN::ConjugateGradient< Size, Precision >::old_y

Function at old_x.

Definition at line 206 of file conjugate_gradient.h.

template<int Size, class Precision = double>
const int TooN::ConjugateGradient< Size, Precision >::size

Dimensionality of the space.

Definition at line 197 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Precision TooN::ConjugateGradient< Size, Precision >::tolerance

Tolerance used to determine if the optimization is complete. Defaults to square root of machine precision.

Definition at line 208 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Vector<Size> TooN::ConjugateGradient< Size, Precision >::x

Current position (best known point).

Definition at line 203 of file conjugate_gradient.h.

template<int Size, class Precision = double>
Precision TooN::ConjugateGradient< Size, Precision >::y

Function at 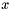$x$.

Definition at line 205 of file conjugate_gradient.h.

The documentation for this struct was generated from the following file:
 All Classes Namespaces Files Functions Variables Typedefs Friends Defines

libtoon
Author(s): Florian Weisshardt
autogenerated on Fri Jan 11 10:09:49 2013