TooN::LU< Size, Precision > Class Template Reference
[Matrix decompositions]
#include <LU.h>
List of all members.
Public Member Functions |
| template<int Rows, class Base > |
| Vector< Size, Precision > | backsub (const Vector< Rows, Precision, Base > &rhs) |
| template<int Rows, int NRHS, class Base > |
| Matrix< Size, NRHS, Precision > | backsub (const Matrix< Rows, NRHS, Precision, Base > &rhs) |
| template<int S1, int S2, class Base > |
| void | compute (const Matrix< S1, S2, Precision, Base > &m) |
| | Perform the LU decompsition of another matrix.
|
| Precision | determinant () const |
| | Calculate the determinant of the matrix.
|
| int | get_info () const |
| | Get the LAPACK info.
|
| Matrix< Size, Size, Precision > | get_inverse () |
const Matrix< Size, Size,
Precision > & | get_lu () const |
| template<int S1, int S2, class Base > |
| | LU (const Matrix< S1, S2, Precision, Base > &m) |
Private Member Functions |
| int | get_sign () const |
Private Attributes |
| int | my_info |
| Vector< Size, int > | my_IPIV |
| Matrix< Size, Size, Precision > | my_lu |
Detailed Description
template<int Size = -1, class Precision = double>
class TooN::LU< Size, Precision >
Performs LU decomposition and back substitutes to solve equations. The LU decomposition is the fastest way of solving the equation 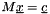 m, but it becomes unstable when
m, but it becomes unstable when 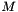 is (nearly) singular (in which cases the SymEigen or SVD decompositions are better). It decomposes a matrix
is (nearly) singular (in which cases the SymEigen or SVD decompositions are better). It decomposes a matrix 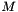 into
into
![\[M = L \times U\]](form_49.png)
where 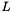 is a lower-diagonal matrix with unit diagonal and
is a lower-diagonal matrix with unit diagonal and 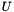 is an upper-diagonal matrix. The library only supports the decomposition of square matrices. It can be used as follows to solve the
is an upper-diagonal matrix. The library only supports the decomposition of square matrices. It can be used as follows to solve the 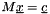 problem as follows:
problem as follows:
The convention LU<> (=LU<-1>) is used to create an LU decomposition whose size is determined at runtime.
Definition at line 69 of file LU.h.
Constructor & Destructor Documentation
template<int Size = -1, class Precision = double>
template<int S1, int S2, class Base >
| TooN::LU< Size, Precision >::LU |
( |
const Matrix< S1, S2, Precision, Base > & |
m |
) |
[inline] |
Construct the LU decomposition of a matrix. This initialises the class, and performs the decomposition immediately.
Definition at line 75 of file LU.h.
Member Function Documentation
template<int Size = -1, class Precision = double>
template<int Rows, class Base >
| Vector<Size,Precision> TooN::LU< Size, Precision >::backsub |
( |
const Vector< Rows, Precision, Base > & |
rhs |
) |
[inline] |
Calculate result of multiplying the inverse of M by a vector. For a vector 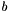 , this calculates
, this calculates 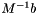 by back substitution (i.e. without explictly calculating the inverse).
by back substitution (i.e. without explictly calculating the inverse).
Definition at line 132 of file LU.h.
template<int Size = -1, class Precision = double>
template<int Rows, int NRHS, class Base >
| Matrix<Size,NRHS,Precision> TooN::LU< Size, Precision >::backsub |
( |
const Matrix< Rows, NRHS, Precision, Base > & |
rhs |
) |
[inline] |
Calculate result of multiplying the inverse of M by another matrix. For a matrix 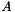 , this calculates
, this calculates 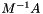 by back substitution (i.e. without explictly calculating the inverse).
by back substitution (i.e. without explictly calculating the inverse).
Definition at line 103 of file LU.h.
template<int Size = -1, class Precision = double>
template<int S1, int S2, class Base >
| void TooN::LU< Size, Precision >::compute |
( |
const Matrix< S1, S2, Precision, Base > & |
m |
) |
[inline] |
Perform the LU decompsition of another matrix.
Definition at line 82 of file LU.h.
template<int Size = -1, class Precision = double>
| Precision TooN::LU< Size, Precision >::determinant |
( |
|
) |
const [inline] |
Calculate the determinant of the matrix.
Definition at line 192 of file LU.h.
template<int Size = -1, class Precision = double>
| int TooN::LU< Size, Precision >::get_info |
( |
|
) |
const [inline] |
Get the LAPACK info.
Definition at line 201 of file LU.h.
template<int Size = -1, class Precision = double>
| Matrix<Size,Size,Precision> TooN::LU< Size, Precision >::get_inverse |
( |
|
) |
[inline] |
Calculate inverse of the matrix. This is not usually needed: if you need the inverse just to multiply it by a matrix or a vector, use one of the backsub() functions, which will be faster.
Definition at line 158 of file LU.h.
template<int Size = -1, class Precision = double>
| const Matrix<Size,Size,Precision>& TooN::LU< Size, Precision >::get_lu |
( |
|
) |
const [inline] |
Returns the L and U matrices. The permutation matrix is not returned. Since L is lower-triangular (with unit diagonal) and U is upper-triangular, these are returned conflated into one matrix, where the diagonal and above parts of the matrix are U and the below-diagonal part, plus a unit diagonal, are L.
Definition at line 177 of file LU.h.
template<int Size = -1, class Precision = double>
| int TooN::LU< Size, Precision >::get_sign |
( |
|
) |
const [inline, private] |
Definition at line 180 of file LU.h.
Member Data Documentation
template<int Size = -1, class Precision = double>
Definition at line 206 of file LU.h.
template<int Size = -1, class Precision = double>
Definition at line 207 of file LU.h.
template<int Size = -1, class Precision = double>
Definition at line 205 of file LU.h.
The documentation for this class was generated from the following file:
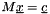 m, but it becomes unstable when
m, but it becomes unstable when 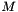 is (nearly) singular (in which cases the SymEigen or SVD decompositions are better). It decomposes a matrix
is (nearly) singular (in which cases the SymEigen or SVD decompositions are better). It decomposes a matrix 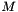 into
into ![\[M = L \times U\]](form_49.png)
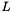 is a lower-diagonal matrix with unit diagonal and
is a lower-diagonal matrix with unit diagonal and 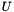 is an upper-diagonal matrix. The library only supports the decomposition of square matrices. It can be used as follows to solve the
is an upper-diagonal matrix. The library only supports the decomposition of square matrices. It can be used as follows to solve the 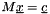 problem as follows:
problem as follows: