TooN::SymEigen< Size, Precision > Class Template Reference
[Matrix decompositions]

#include <SymEigen.h>

List of all members.

Public Member Functions

template<int R, int C, typename P , typename B >
Matrix< Size, C, Precision > backsub (const Matrix< R, C, P, B > &rhs) const
template<int S, typename P , typename B >
Vector< Size, Precision > backsub (const Vector< S, P, B > &rhs) const
template<int R, int C, typename B >
void compute (const Matrix< R, C, Precision, B > &m)
 Perform the eigen decomposition of a matrix.
Precision get_determinant () const
 Get the determinant of the matrix.
const Vector< Size, Precision > & get_evalues () const
Vector< Size, Precision > & get_evalues ()
const Matrix< Size, Size,
Precision > & 		get_evectors () const
Matrix< Size, Size, Precision > & get_evectors ()
Vector< Size, Precision > get_inv_diag (const double condition) const
Matrix< Size, Size, Precision > get_isqrtm (const double condition=Internal::symeigen_condition_no) const
Matrix< Size, Size, Precision > get_pinv (const double condition=Internal::symeigen_condition_no) const
Matrix< Size, Size, Precision > get_sqrtm () const
bool is_negdef () const
 Is the matrix negative definite?
bool is_posdef () const
 Is the matrix positive definite?
template<int R, int C, typename B >
 SymEigen (const Matrix< R, C, Precision, B > &m)
 SymEigen (int m)
 SymEigen ()

Private Attributes

Vector< Size, Precision > my_evalues
Matrix< Size, Size, Precision > my_evectors

Detailed Description

template<int Size = Dynamic, typename Precision = double>
class TooN::SymEigen< Size, Precision >

Performs eigen decomposition of a matrix. Real symmetric (and hence square matrices) can be decomposed into

\[M = U \times \Lambda \times U^T\]

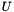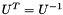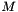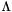where $U$ is an orthogonal matrix (and hence $U^T = U^{-1}$) whose columns are the eigenvectors of $M$ and $\Lambda$ is a diagonal matrix whose entries are the eigenvalues of 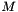$M$. These quantities are often of use directly, and can be obtained as follows: 

// construct M
Matrix<3> M(3,3);
M[0]=makeVector(4,0,2);
M[1]=makeVector(0,5,3);
M[2]=makeVector(2,3,6);

// create the eigen decomposition of M
SymEigen<3> eigM(M);
cout << "A=" << M << endl;
cout << "(E,v)=eig(A)" << endl;
// print the smallest eigenvalue
cout << "v[0]=" << eigM.get_evalues()[0] << endl;
// print the associated eigenvector
cout << "E[0]=" << eigM.get_evectors()[0] << endl;

Further, provided the eigenvalues are nonnegative, the square root of a matrix and its inverse can also be obtained, 

// print the square root of the matrix.
cout << "R=sqrtm(A)=" << eigM.get_sqrtm() << endl;
// print the square root of the matrix squared.
cout << "(should equal A), R^T*R="
     << eigM.get_sqrtm().T() * eigM.get_sqrtm() << endl;
// print the inverse of the matrix.
cout << "A^-1=" << eigM.get_pinv() << endl;
// print the inverse square root of the matrix.
cout << "C=isqrtm(A)=" << eigM.get_isqrtm() << endl;
// print the inverse square root of the matrix squared.
cout << "(should equal A^-1), C^T*C="
     << eigM.get_isqrtm().T() * eigM.get_isqrtm() << endl;

This decomposition is very similar to the SVD (q.v.), and can be used to solve equations using backsub() or get_pinv(), with the same treatment of condition numbers.

SymEigen<> (= SymEigen<-1>) can be used to create an eigen decomposition whose size is determined at run-time.

Definition at line 260 of file SymEigen.h.

Constructor & Destructor Documentation

template<int Size = Dynamic, typename Precision = double>
TooN::SymEigen< Size, Precision >::SymEigen (  )  [inline]

Definition at line 262 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
TooN::SymEigen< Size, Precision >::SymEigen ( int  m  )  [inline]

Initialise this eigen decomposition but do no immediately perform a decomposition.

Parameters:
m The size of the matrix to perform the eigen decomposition on.

Definition at line 268 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
template<int R, int C, typename B >
TooN::SymEigen< Size, Precision >::SymEigen ( const Matrix< R, C, Precision, B > &  m  )  [inline]

Construct the eigen decomposition of a matrix. This initialises the class, and performs the decomposition immediately.

Definition at line 273 of file SymEigen.h.

Member Function Documentation

template<int Size = Dynamic, typename Precision = double>
template<int R, int C, typename P , typename B >
Matrix<Size,C, Precision> TooN::SymEigen< Size, Precision >::backsub ( const Matrix< R, C, P, B > &  rhs  )  const [inline]

Calculate result of multiplying the (pseudo-)inverse of M by another matrix. For a matrix 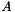$A$, this calculates 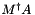$M^{\dagger}A$ by back substitution (i.e. without explictly calculating the (pseudo-)inverse). See the SVD detailed description for a description of condition variables.

Definition at line 299 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
template<int S, typename P , typename B >
Vector<Size, Precision> TooN::SymEigen< Size, Precision >::backsub ( const Vector< S, P, B > &  rhs  )  const [inline]

Calculate result of multiplying the (pseudo-)inverse of M by a vector. For a vector 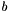$b$, this calculates 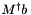$M^{\dagger}b$ by back substitution (i.e. without explictly calculating the (pseudo-)inverse). See the SVD detailed description for a description of condition variables.

Definition at line 290 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
template<int R, int C, typename B >
void TooN::SymEigen< Size, Precision >::compute ( const Matrix< R, C, Precision, B > &  m  )  [inline]

Perform the eigen decomposition of a matrix.

Definition at line 279 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
Precision TooN::SymEigen< Size, Precision >::get_determinant (  )  const [inline]

Get the determinant of the matrix.

Definition at line 370 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
const Vector<Size, Precision>& TooN::SymEigen< Size, Precision >::get_evalues (  )  const [inline]

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

Definition at line 349 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
Vector<Size, Precision>& TooN::SymEigen< Size, Precision >::get_evalues (  )  [inline]

Returns the eigenvalues of the matrix. The eigenvalues are listed in order, from the smallest to the largest. These are also the diagonal values of the matrix 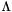$\Lambda$.

Definition at line 346 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
const Matrix<Size,Size,Precision>& TooN::SymEigen< Size, Precision >::get_evectors (  )  const [inline]

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

Definition at line 340 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
Matrix<Size,Size,Precision>& TooN::SymEigen< Size, Precision >::get_evectors (  )  [inline]

Returns the eigenvectors of the matrix. This returns 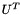$U^T$, so that the rows of the matrix are the eigenvectors, which can be extracted using usual Matrix::operator[]() subscript operator. They are returned in order of the size of the corresponding eigenvalue, i.e. the vector with the largest eigenvalue is first.

Definition at line 336 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
Vector<Size, Precision> TooN::SymEigen< Size, Precision >::get_inv_diag ( const double  condition  )  const [inline]

Calculates the reciprocals of the eigenvalues of the matrix. The vector invdiag lists the eigenvalues in order, from the largest (i.e. smallest reciprocal) to the smallest. These are also the diagonal values of the matrix 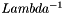$Lambda^{-1}$. Any eigenvalues which are too small are set to zero (see the SVD detailed description for a description of the and condition variables).

Definition at line 318 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
Matrix<Size, Size, Precision> TooN::SymEigen< Size, Precision >::get_isqrtm ( const double  condition = Internal::symeigen_condition_no  )  const [inline]

Calculate the inverse square root of a matrix which is a matrix M such that M.T*M=A^-1.

Any square-rooted eigenvalues which are too small are set to zero (see the SVD detailed description for a description of the condition variables).

Definition at line 396 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
Matrix<Size, Size, Precision> TooN::SymEigen< Size, Precision >::get_pinv ( const double  condition = Internal::symeigen_condition_no  )  const [inline]

Calculate (pseudo-)inverse of the matrix. This is not usually needed: if you need the inverse just to multiply it by a matrix or a vector, use one of the backsub() functions, which will be faster. See the SVD detailed description for a description of the pseudo-inverse and condition variables.

Definition at line 308 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
Matrix<Size, Size, Precision> TooN::SymEigen< Size, Precision >::get_sqrtm (  )  const [inline]

Calculate the square root of a matrix which is a matrix M such that M.T*M=A.

Definition at line 380 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
bool TooN::SymEigen< Size, Precision >::is_negdef (  )  const [inline]

Is the matrix negative definite?

Definition at line 361 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
bool TooN::SymEigen< Size, Precision >::is_posdef (  )  const [inline]

Is the matrix positive definite?

Definition at line 352 of file SymEigen.h.

Member Data Documentation

template<int Size = Dynamic, typename Precision = double>
Vector<Size, Precision> TooN::SymEigen< Size, Precision >::my_evalues [private]

Definition at line 418 of file SymEigen.h.

template<int Size = Dynamic, typename Precision = double>
Matrix<Size,Size,Precision> TooN::SymEigen< Size, Precision >::my_evectors [private]

Definition at line 416 of file SymEigen.h.

The documentation for this class was generated from the following file:
 All Classes Namespaces Files Functions Variables Typedefs Friends Defines

libtoon
Author(s): Florian Weisshardt
autogenerated on Fri Jan 11 10:09:50 2013