#include <SVD.h>
Public Member Functions | |
| template<int Size, typename P2 , typename B2 > | |
| Vector< Cols, typename Internal::MultiplyType < Precision, P2 >::type > | backsub (const Vector< Size, P2, B2 > &rhs, const Precision condition=condition_no) |
| template<int Rows2, int Cols2, typename P2 , typename B2 > | |
| Matrix< Cols, Cols2, typename Internal::MultiplyType < Precision, P2 >::type > | backsub (const Matrix< Rows2, Cols2, P2, B2 > &rhs, const Precision condition=condition_no) |
| template<int R2, int C2, typename P2 , typename B2 > | |
| void | compute (const Matrix< R2, C2, P2, B2 > &m) |
| Compute the SVD decomposition of M, typically used after the default constructor. | |
| Precision | determinant () |
| Vector< Min_Dim, Precision > & | get_diagonal () |
| Return the singular values as a vector. | |
| void | get_inv_diag (Vector< Min_Dim > &inv_diag, const Precision condition) |
| Matrix< Cols, Rows > | get_pinv (const Precision condition=condition_no) |
| Matrix< Rows, Min_Dim, Precision, Reference::RowMajor > | get_U () |
| Matrix< Min_Dim, Cols, Precision, Reference::RowMajor > | get_VT () |
| int | rank (const Precision condition=condition_no) |
| template<int R2, int C2, typename P2 , typename B2 > | |
| SVD (const Matrix< R2, C2, P2, B2 > &m) | |
| SVD (int rows, int cols) | |
| constructor for Rows=-1 or Cols=-1 (or both) | |
| SVD () | |
| default constructor for Rows>0 and Cols>0 | |
Private Member Functions | |
| void | do_compute () |
| bool | is_vertical () |
| int | min_dim () |
Private Attributes | |
| Matrix< Rows, Cols, Precision, RowMajor > | my_copy |
| Vector< Min_Dim, Precision > | my_diagonal |
| Matrix< Min_Dim, Min_Dim, Precision, RowMajor > | my_square |
Static Private Attributes | |
| static const int | Min_Dim = Rows<Cols?Rows:Cols |
Performs SVD and back substitute to solve equations. Singular value decompositions are more robust than LU decompositions in the face of singular or nearly singular matrices. They decompose a matrix (of any shape) 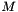 into:
into:
![\[M = U \times D \times V^T\]](form_109.png)
where 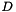 is a diagonal matrix of positive numbers whose dimension is the minimum of the dimensions of
is a diagonal matrix of positive numbers whose dimension is the minimum of the dimensions of 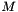 . If
. If 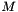 is tall and thin (more rows than columns) then
is tall and thin (more rows than columns) then 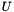 has the same shape as
has the same shape as 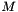 and
and 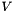 is square (vice-versa if
is square (vice-versa if 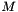 is short and fat). The columns of
is short and fat). The columns of 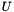 and the rows of
and the rows of 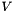 are orthogonal and of unit norm (so one of them lies in SO(N)). The inverse of
are orthogonal and of unit norm (so one of them lies in SO(N)). The inverse of 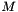 (or pseudo-inverse if
(or pseudo-inverse if 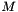 is not square) is then given by
is not square) is then given by
![\[M^{\dagger} = V \times D^{-1} \times U^T\]](form_112.png)
If 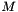 is nearly singular then the diagonal matrix
is nearly singular then the diagonal matrix 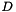 has some small values (relative to its largest value) and these terms dominate
has some small values (relative to its largest value) and these terms dominate 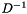 . To deal with this problem, the inverse is conditioned by setting a maximum ratio between the largest and smallest values in
. To deal with this problem, the inverse is conditioned by setting a maximum ratio between the largest and smallest values in 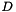 (passed as the
(passed as the condition parameter to the various functions). Any values which are too small are set to zero in the inverse (rather than a large number)
It can be used as follows to solve the 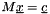 problem as follows:
problem as follows:
// construct M Matrix<3> M; M[0] = makeVector(1,2,3); M[1] = makeVector(4,5,6); M[2] = makeVector(7,8.10); // construct c Vector<3> c; c = 2,3,4; // create the SVD decomposition of M SVD<3> svdM(M); // compute x = M^-1 * c Vector<3> x = svdM.backsub(c);
SVD<> (= SVD<-1>) can be used to create an SVD whose size is determined at run-time.
Definition at line 88 of file SVD.h.
| Vector<Cols, typename Internal::MultiplyType<Precision,P2>::type > TooN::SVD< Rows, Cols, Precision >::backsub | ( | const Vector< Size, P2, B2 > & | rhs, | |
| const Precision | condition = condition_no | |||
| ) | [inline] |
| Matrix<Cols,Cols2, typename Internal::MultiplyType<Precision,P2>::type > TooN::SVD< Rows, Cols, Precision >::backsub | ( | const Matrix< Rows2, Cols2, P2, B2 > & | rhs, | |
| const Precision | condition = condition_no | |||
| ) | [inline] |
| Precision TooN::SVD< Rows, Cols, Precision >::determinant | ( | ) | [inline] |
| void TooN::SVD< Rows, Cols, Precision >::do_compute | ( | ) | [inline, private] |
| void TooN::SVD< Rows, Cols, Precision >::get_inv_diag | ( | Vector< Min_Dim > & | inv_diag, | |
| const Precision | condition | |||
| ) | [inline] |
Return the pesudo-inverse diagonal. The reciprocal of the diagonal elements is returned if the elements are well scaled with respect to the largest element, otherwise 0 is returned.
| inv_diag | Vector in which to return the inverse diagonal. | |
| condition | Elements must be larger than this factor times the largest diagonal element to be considered well scaled. |
| Matrix<Cols,Rows> TooN::SVD< Rows, Cols, Precision >::get_pinv | ( | const Precision | condition = condition_no |
) | [inline] |
Calculate (pseudo-)inverse of the matrix. This is not usually needed: if you need the inverse just to multiply it by a matrix or a vector, use one of the backsub() functions, which will be faster. See the detailed description of the pseudo-inverse and condition variables.
| Matrix<Rows,Min_Dim,Precision,Reference::RowMajor> TooN::SVD< Rows, Cols, Precision >::get_U | ( | ) | [inline] |
| Matrix<Min_Dim,Cols,Precision,Reference::RowMajor> TooN::SVD< Rows, Cols, Precision >::get_VT | ( | ) | [inline] |
| bool TooN::SVD< Rows, Cols, Precision >::is_vertical | ( | ) | [inline, private] |
| int TooN::SVD< Rows, Cols, Precision >::min_dim | ( | ) | [inline, private] |
| int TooN::SVD< Rows, Cols, Precision >::rank | ( | const Precision | condition = condition_no |
) | [inline] |
Vector<Min_Dim,Precision> TooN::SVD< Rows, Cols, Precision >::my_diagonal [private] |