Math operations (Mathematical operations) More...


Go to the source code of this file.
Defines | |
| #define | VL_E 2.718281828459045 |
| Euler constant. | |
| #define | VL_EPSILON_D 2.220446049250313e-16 |
| IEEE double precision epsilon (math constant) | |
| #define | VL_EPSILON_F 1.19209290E-07F |
| IEEE single precision epsilon (math constant) | |
| #define | VL_FAST_SQRT_UI(T, SFX) |
| #define | VL_INFINITY_D (vl_infinity_d.value) |
| IEEE double precision positive infinity (not signaling) | |
| #define | VL_INFINITY_F (vl_infinity_f.value) |
| IEEE single precision positive infinity (not signaling) | |
| #define | VL_LOG_OF_2 0.693147180559945 |
| Logarithm of 2 (math constant) | |
| #define | VL_NAN_D (vl_nan_d.value) |
| IEEE double precision NaN (not signaling) | |
| #define | VL_NAN_F (vl_nan_f.value) |
| IEEE single precision NaN (not signaling) | |
| #define | VL_PI 3.141592653589793 |
| Pi (math constant) | |
Typedefs | |
| typedef double(* | VlDoubleVector3ComparisonFunction )(vl_size dimension, double const *X, double const *Y, double const *Z) |
| Pointer to a function to compare 3 vectors of doubles. | |
| typedef double(* | VlDoubleVectorComparisonFunction )(vl_size dimension, double const *X, double const *Y) |
| Pointer to a function to compare vectors of doubles. | |
| typedef float(* | VlFloatVector3ComparisonFunction )(vl_size dimension, float const *X, float const *Y, float const *Z) |
| Pointer to a function to compare 3 vectors of doubles. | |
| typedef float(* | VlFloatVectorComparisonFunction )(vl_size dimension, float const *X, float const *Y) |
| Pointer to a function to compare vectors of floats. | |
| typedef enum _VlVectorComparisonType | VlVectorComparisonType |
| Vector comparison types. | |
Enumerations | |
| enum | _VlVectorComparisonType { VlDistanceL1, VlDistanceL2, VlDistanceChi2, VlDistanceHellinger, VlDistanceJS, VlDistanceMahalanobis, VlKernelL1, VlKernelL2, VlKernelChi2, VlKernelHellinger, VlKernelJS } |
| Vector comparison types. More... | |
Functions | |
| VL_INLINE double | vl_abs_d (double x) |
Fast abs(x) | |
| VL_INLINE float | vl_abs_f (float x) |
Fast abs(x) | |
| VL_INLINE long int | vl_ceil_d (double x) |
| Ceil and convert to integer. | |
| VL_INLINE long int | vl_ceil_f (float x) |
| Ceil and convert to integer. | |
| VL_EXPORT void | vl_eval_vector_comparison_on_all_pairs_d (double *result, vl_size dimension, double const *X, vl_size numDataX, double const *Y, vl_size numDataY, VlDoubleVectorComparisonFunction function) |
| Evaluate vector comparison function on all vector pairs. | |
| VL_EXPORT void | vl_eval_vector_comparison_on_all_pairs_f (float *result, vl_size dimension, float const *X, vl_size numDataX, float const *Y, vl_size numDataY, VlFloatVectorComparisonFunction function) |
| Evaluate vector comparison function on all vector pairs. | |
| VL_INLINE double | vl_fast_atan2_d (double y, double x) |
Fast atan2 approximation. | |
| VL_INLINE float | vl_fast_atan2_f (float y, float x) |
Fast atan2 approximation. | |
| VL_INLINE double | vl_fast_resqrt_d (double x) |
Fast resqrt approximation. | |
| VL_INLINE float | vl_fast_resqrt_f (float x) |
Fast resqrt approximation. | |
| VL_INLINE double | vl_fast_sqrt_d (float x) |
Fast sqrt approximation. | |
| VL_INLINE float | vl_fast_sqrt_f (float x) |
Fast sqrt approximation. | |
| VL_INLINE vl_uint16 | vl_fast_sqrt_ui16 (vl_uint16 x) |
Fast sqrt approximation. | |
| VL_INLINE vl_uint32 | vl_fast_sqrt_ui32 (vl_uint32 x) |
Fast sqrt approximation. | |
| VL_INLINE vl_uint64 | vl_fast_sqrt_ui64 (vl_uint64 x) |
Fast integer sqrt approximation. | |
| VL_INLINE vl_uint8 | vl_fast_sqrt_ui8 (vl_uint8 x) |
Fast sqrt approximation. | |
| VL_INLINE long int | vl_floor_d (double x) |
| Floor and convert to integer. | |
| VL_INLINE long int | vl_floor_f (float x) |
| Floor and convert to integer. | |
| VL_EXPORT int | vl_gaussian_elimination (double *A, vl_size numRows, vl_size numColumns) |
| VL_EXPORT VlDoubleVector3ComparisonFunction | vl_get_vector_3_comparison_function_d (VlVectorComparisonType type) |
| VL_EXPORT VlFloatVector3ComparisonFunction | vl_get_vector_3_comparison_function_f (VlVectorComparisonType type) |
| VL_EXPORT VlDoubleVectorComparisonFunction | vl_get_vector_comparison_function_d (VlVectorComparisonType type) |
| Get vector comparison function from comparison type. | |
| VL_EXPORT VlFloatVectorComparisonFunction | vl_get_vector_comparison_function_f (VlVectorComparisonType type) |
| Get vector comparison function from comparison type. | |
| VL_INLINE char const * | vl_get_vector_comparison_type_name (int type) |
| Get the symbolic name of a vector comparison type. | |
| VL_INLINE vl_bool | vl_is_inf_d (double x) |
| VL_INLINE vl_bool | vl_is_inf_f (float x) |
| Check whether a floating point value is infinity. | |
| VL_INLINE vl_bool | vl_is_nan_d (double x) |
| VL_INLINE vl_bool | vl_is_nan_f (float x) |
| Check whether a floating point value is NaN. | |
| VL_EXPORT void | vl_lapack_dlasv2 (double *smin, double *smax, double *sv, double *cv, double *su, double *cu, double f, double g, double h) |
| VL_INLINE double | vl_log2_d (double x) |
| Base-2 logaritghm. | |
| VL_INLINE float | vl_log2_f (float x) |
| VL_INLINE double | vl_mod_2pi_d (double x) |
Fast mod(x, 2 * VL_PI) | |
| VL_INLINE float | vl_mod_2pi_f (float x) |
Fast mod(x, 2 * VL_PI) | |
| VL_INLINE long int | vl_round_d (double x) |
| Round. | |
| VL_INLINE long int | vl_round_f (float x) |
| Round. | |
| VL_EXPORT int | vl_solve_linear_system_2 (double *x, double const *A, double const *b) |
| VL_EXPORT int | vl_solve_linear_system_3 (double *x, double const *A, double const *b) |
| VL_INLINE double | vl_sqrt_d (double x) |
| Square root. | |
| VL_INLINE float | vl_sqrt_f (float x) |
| VL_EXPORT void | vl_svd2 (double *S, double *U, double *V, double const *M) |
Variables | |
| union { | |
| vl_uint64 raw | |
| double value | |
| } | vl_infinity_d |
| union { | |
| vl_uint32 raw | |
| float value | |
| } | vl_infinity_f |
| union { | |
| vl_uint64 raw | |
| double value | |
| } | vl_nan_d |
| union { | |
| vl_uint32 raw | |
| float value | |
| } | vl_nan_f |
Detailed Description
Math operations (Mathematical operations)
Definition in file mathop.h.
Define Documentation
| #define VL_EPSILON_D 2.220446049250313e-16 |
IEEE double precision epsilon (math constant)
1.0 + VL_EPSILON_D is the smallest representable double precision number greater than 1.0. Numerically, VL_EPSILON_D is equal to 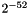 .
.
| #define VL_EPSILON_F 1.19209290E-07F |
IEEE single precision epsilon (math constant)
1.0F + VL_EPSILON_F is the smallest representable single precision number greater than 1.0F. Numerically, VL_EPSILON_F is equal to 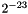 .
.
| #define VL_FAST_SQRT_UI | ( | T, | |
| SFX | |||
| ) |
VL_INLINE T \ vl_fast_sqrt_ ## SFX (T x) \ { \ T y = 0 ; \ T tmp = 0 ; \ int twice_k ; \ for (twice_k = 8 * sizeof(T) - 2 ; \ twice_k >= 0 ; twice_k -= 2) { \ y <<= 1 ; /* y = 2 * y */ \ tmp = (2*y + 1) << twice_k ; \ if (x >= tmp) { \ x -= tmp ; \ y += 1 ; \ } \ } \ return y ; \ }
| #define VL_INFINITY_D (vl_infinity_d.value) |
| #define VL_INFINITY_F (vl_infinity_f.value) |
| #define VL_LOG_OF_2 0.693147180559945 |
| #define VL_NAN_D (vl_nan_d.value) |
| #define VL_NAN_F (vl_nan_f.value) |
Typedef Documentation
| typedef enum _VlVectorComparisonType VlVectorComparisonType |
Enumeration Type Documentation
Vector comparison types.
- Enumerator:
Function Documentation
| VL_INLINE double vl_abs_d | ( | double | x | ) |
| VL_INLINE float vl_abs_f | ( | float | x | ) |
| VL_INLINE long int vl_ceil_d | ( | double | x | ) |
| VL_INLINE long int vl_ceil_f | ( | float | x | ) |
| vl_eval_vector_comparison_on_all_pairs_d | ( | double * | result, |
| vl_size | dimension, | ||
| double const * | X, | ||
| vl_size | numDataX, | ||
| double const * | Y, | ||
| vl_size | numDataY, | ||
| VlDoubleVectorComparisonFunction | function | ||
| ) |
Evaluate vector comparison function on all vector pairs.
| vl_eval_vector_comparison_on_all_pairs_f | ( | float * | result, |
| vl_size | dimension, | ||
| float const * | X, | ||
| vl_size | numDataX, | ||
| float const * | Y, | ||
| vl_size | numDataY, | ||
| VlFloatVectorComparisonFunction | function | ||
| ) |
Evaluate vector comparison function on all vector pairs.
- Parameters:
-
result comparison matrix (output). dimension number of vector components (rows of X and Y). X data matrix X. Y data matrix Y. numDataX number of vectors in X (columns of X) numDataY number of vectros in Y (columns of Y) function vector comparison function.
The function evaluates function on all pairs of columns from matrices X and Y, filling a numDataX by numDataY matrix.
If Y is a null pointer the function compares all columns from X with themselves.
| VL_INLINE double vl_fast_atan2_d | ( | double | y, |
| double | x | ||
| ) |
| VL_INLINE float vl_fast_atan2_f | ( | float | y, |
| float | x | ||
| ) |
Fast atan2 approximation.
------------------------------------------------------------------
- Parameters:
-
y argument. x argument.
The function computes a relatively rough but fast approximation of atan2(y,x).
- Algorithm
The algorithm approximates the function 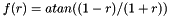 ,
, ![$ r \in [-1,1] $](form_175.png) with a third order polynomial
with a third order polynomial 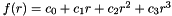 . To fit the polynomial we impose the constraints
. To fit the polynomial we impose the constraints
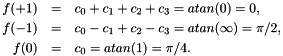
The last degree of freedom is fixed by minimizing the 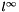 error, which yields
error, which yields
![\[ c_0=\pi/4, \quad c_1=-0.9675, \quad c_2=0, \quad c_3=0.1821, \]](form_179.png)
with maximum error of 0.0061 radians at 0.35 degrees.
- Returns:
- Approximation of
atan2(y,x).
| VL_INLINE double vl_fast_resqrt_d | ( | double | x | ) |
| VL_INLINE float vl_fast_resqrt_f | ( | float | x | ) |
Fast resqrt approximation.
------------------------------------------------------------------
- Parameters:
-
x argument.
- Returns:
- approximation of
resqrt(x).
The function quickly computes an approximation of 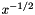 .
.
- Algorithm
The goal is to compute 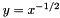 , which we do by finding the solution of
, which we do by finding the solution of 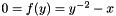 by two Newton steps. Each Newton iteration is given by
by two Newton steps. Each Newton iteration is given by
![\[ y \leftarrow y - \frac{f(y)}{\frac{df(y)}{dy}} = y + \frac{1}{2} (y-xy^3) = \frac{y}{2} \left( 3 - xy^2 \right) \]](form_183.png)
which yields a simple polynomial update rule.
The clever bit (attributed to either J. Carmack or G. Tarolli) is the way an initial guess 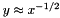 is chosen.
is chosen.
- See also:
- Inverse Sqare Root.
| VL_INLINE double vl_fast_sqrt_d | ( | float | x | ) |
Fast sqrt approximation.
Fast sqrt approximation.
------------------------------------------------------------------
- Parameters:
-
x argument.
- Returns:
- approximation of
sqrt(x).
The function uses vl_fast_resqrt_f (or vl_fast_resqrt_d) to compute x * vl_fast_resqrt_f(x).
| VL_INLINE float vl_fast_sqrt_f | ( | float | x | ) |
Fast sqrt approximation.
------------------------------------------------------------------
- Parameters:
-
x argument.
- Returns:
- approximation of
sqrt(x).
The function uses vl_fast_resqrt_f (or vl_fast_resqrt_d) to compute x * vl_fast_resqrt_f(x).
| VL_INLINE vl_uint16 vl_fast_sqrt_ui16 | ( | vl_uint16 | x | ) |
Fast sqrt approximation.
Fast integer sqrt approximation.
- Parameters:
-
x non-negative integer.
- Returns:
- largest integer $y$ such that $y^2 x$.
- See also:
- Algorithm
| VL_INLINE vl_uint32 vl_fast_sqrt_ui32 | ( | vl_uint32 | x | ) |
Fast sqrt approximation.
Fast integer sqrt approximation.
- Parameters:
-
x non-negative integer.
- Returns:
- largest integer $y$ such that $y^2 x$.
- See also:
- Algorithm
| VL_INLINE vl_uint64 vl_fast_sqrt_ui64 | ( | vl_uint64 | x | ) |
Fast integer sqrt approximation.
- Parameters:
-
x non-negative integer.
- Returns:
- largest integer $y$ such that $y^2 x$.
- See also:
- Algorithm
| VL_INLINE vl_uint8 vl_fast_sqrt_ui8 | ( | vl_uint8 | x | ) |
Fast sqrt approximation.
Fast integer sqrt approximation.
- Parameters:
-
x non-negative integer.
- Returns:
- largest integer $y$ such that $y^2 x$.
- See also:
- Algorithm
| VL_INLINE long int vl_floor_d | ( | double | x | ) |
| VL_INLINE long int vl_floor_f | ( | float | x | ) |
| VL_EXPORT int vl_gaussian_elimination | ( | double * | A, |
| vl_size | numRows, | ||
| vl_size | numColumns | ||
| ) |
| VL_EXPORT VlDoubleVector3ComparisonFunction vl_get_vector_3_comparison_function_d | ( | VlVectorComparisonType | type | ) |
| VL_EXPORT VlFloatVector3ComparisonFunction vl_get_vector_3_comparison_function_f | ( | VlVectorComparisonType | type | ) |
Get vector comparison function from comparison type.
- See also:
- vl_get_vector_comparison_function_f
Get vector comparison function from comparison type.
- Parameters:
-
type vector comparison type.
- Returns:
- comparison function.
| VL_INLINE char const* vl_get_vector_comparison_type_name | ( | int | type | ) |
| VL_INLINE vl_bool vl_is_inf_d | ( | double | x | ) |
| VL_INLINE vl_bool vl_is_inf_f | ( | float | x | ) |
| VL_INLINE vl_bool vl_is_nan_d | ( | double | x | ) |
| VL_INLINE vl_bool vl_is_nan_f | ( | float | x | ) |
| VL_EXPORT void vl_lapack_dlasv2 | ( | double * | smin, |
| double * | smax, | ||
| double * | sv, | ||
| double * | cv, | ||
| double * | su, | ||
| double * | cu, | ||
| double | f, | ||
| double | g, | ||
| double | h | ||
| ) |
| VL_INLINE double vl_log2_d | ( | double | x | ) |
| VL_INLINE float vl_log2_f | ( | float | x | ) |
| VL_INLINE double vl_mod_2pi_d | ( | double | x | ) |
| VL_INLINE float vl_mod_2pi_f | ( | float | x | ) |
Fast mod(x, 2 * VL_PI)
- Parameters:
-
x input value.
- Returns:
mod(x, 2 * VL_PI)
The function is optimized for small absolute values of x.
The result is guaranteed to be not smaller than 0. However, due to finite numerical precision and rounding errors, the result can be equal to 2 * VL_PI (for instance, if x is a very small negative number).
| VL_INLINE long int vl_round_d | ( | double | x | ) |
| VL_INLINE long int vl_round_f | ( | float | x | ) |
| VL_EXPORT int vl_solve_linear_system_2 | ( | double * | x, |
| double const * | A, | ||
| double const * | b | ||
| ) |
| VL_EXPORT int vl_solve_linear_system_3 | ( | double * | x, |
| double const * | A, | ||
| double const * | b | ||
| ) |
| VL_INLINE double vl_sqrt_d | ( | double | x | ) |
| VL_INLINE float vl_sqrt_f | ( | float | x | ) |
Variable Documentation
union { ... } vl_infinity_d [static] |
union { ... } vl_infinity_f [static] |
union { ... } vl_nan_d [static] |
union { ... } vl_nan_f [static] |