Left-Invariant Extended Kalman Filter on a Lie group G. More...
#include <InvariantEKF.h>
Public Types | |
| using | Base = LieGroupEKF< G > |
| Base class type. More... | |
| using | Covariance = typename Base::Covariance |
| Covariance matrix type. Eigen::Matrix<double, Dim, Dim>. More... | |
| using | Jacobian = typename Base::Jacobian |
| Jacobian for group-specific operations like AdjointMap. Eigen::Matrix<double, Dim, Dim>. More... | |
| using | TangentVector = typename Base::TangentVector |
 Public Types inherited from gtsam::LieGroupEKF< G > Public Types inherited from gtsam::LieGroupEKF< G > | |
| using | Base = ManifoldEKF< G > |
| Base class type. More... | |
| using | Covariance = typename Base::Covariance |
| template<typename Dynamics > | |
| using | enable_if_dynamics = std::enable_if_t< !std::is_convertible_v< Dynamics, TangentVector > &&std::is_invocable_r_v< TangentVector, Dynamics, const G &, OptionalJacobian< Dim, Dim > & > > |
| template<typename Control , typename Dynamics > | |
| using | enable_if_full_dynamics = std::enable_if_t< std::is_invocable_r_v< TangentVector, Dynamics, const G &, const Control &, OptionalJacobian< Dim, Dim > & > > |
| using | Jacobian = typename Base::Jacobian |
| Jacobian for group operations (Adjoint, Expmap derivatives, F). More... | |
| using | TangentVector = typename Base::TangentVector |
 Public Types inherited from gtsam::ManifoldEKF< G > Public Types inherited from gtsam::ManifoldEKF< G > | |
| using | Covariance = Eigen::Matrix< double, Dim, Dim > |
| Covariance matrix type (P, Q). More... | |
| using | Jacobian = Eigen::Matrix< double, Dim, Dim > |
| State transition Jacobian type (F). More... | |
| using | TangentVector = typename traits< G >::TangentVector |
| Tangent vector type for the manifold M. More... | |
Public Member Functions | |
| InvariantEKF (const G &X0, const Covariance &P0) | |
| void | predict (const G &U, const Covariance &Q) |
| void | predict (const TangentVector &u, double dt, const Covariance &Q) |
 Public Member Functions inherited from gtsam::LieGroupEKF< G > Public Member Functions inherited from gtsam::LieGroupEKF< G > | |
| LieGroupEKF (const G &X0, const Covariance &P0) | |
| template<typename Control , typename Dynamics , typename = enable_if_full_dynamics<Control, Dynamics>> | |
| void | predict (Dynamics &&f, const Control &u, double dt, const Covariance &Q) |
| template<typename Dynamics , typename = enable_if_dynamics<Dynamics>> | |
| void | predict (Dynamics &&f, double dt, const Covariance &Q) |
| template<typename Control , typename Dynamics , typename = enable_if_full_dynamics<Control, Dynamics>> | |
| G | predictMean (Dynamics &&f, const Control &u, double dt, OptionalJacobian< Dim, Dim > A={}) const |
| template<typename Dynamics , typename = enable_if_dynamics<Dynamics>> | |
| G | predictMean (Dynamics &&f, double dt, OptionalJacobian< Dim, Dim > A={}) const |
 Public Member Functions inherited from gtsam::ManifoldEKF< G > Public Member Functions inherited from gtsam::ManifoldEKF< G > | |
| const Covariance & | covariance () const |
| int | dimension () const |
| ManifoldEKF (const G &X0, const Covariance &P0) | |
| void | predict (const G &X_next, const Jacobian &F, const Covariance &Q) |
| const G & | state () const |
| void | update (const Measurement &prediction, const Eigen::Matrix< double, traits< Measurement >::dimension, Dim > &H, const Measurement &z, const Eigen::Matrix< double, traits< Measurement >::dimension, traits< Measurement >::dimension > &R) |
| void | update (MeasurementFunction &&h, const Measurement &z, const Eigen::Matrix< double, traits< Measurement >::dimension, traits< Measurement >::dimension > &R) |
| virtual | ~ManifoldEKF ()=default |
Additional Inherited Members | |
 Static Public Attributes inherited from gtsam::LieGroupEKF< G > Static Public Attributes inherited from gtsam::LieGroupEKF< G > | |
| static constexpr int | Dim = Base::Dim |
| Compile-time dimension of G. More... | |
 Static Public Attributes inherited from gtsam::ManifoldEKF< G > Static Public Attributes inherited from gtsam::ManifoldEKF< G > | |
| static constexpr int | Dim |
| Compile-time dimension of the manifold M. More... | |
 Protected Attributes inherited from gtsam::ManifoldEKF< G > Protected Attributes inherited from gtsam::ManifoldEKF< G > | |
| int | n_ |
| Runtime tangent space dimension of M. More... | |
| Covariance | P_ |
| Covariance (Eigen::Matrix<double, Dim, Dim>). More... | |
| G | X_ |
| Manifold state estimate. More... | |
Detailed Description
template<typename G>
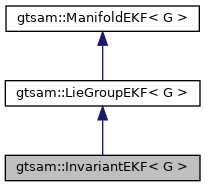
class gtsam::InvariantEKF< G >
Left-Invariant Extended Kalman Filter on a Lie group G.
- Template Parameters
-
G Lie group type (must satisfy LieGroup concept).
This filter inherits from LieGroupEKF but restricts the prediction interface to only the left-invariant prediction methods:
- Prediction via group composition:
predict(const G& U, const Covariance& Q) - Prediction via tangent control vector:
predict(const TangentVector& u, double dt, const Covariance& Q)
The state-dependent prediction methods from LieGroupEKF are hidden. The update step remains the same as in ManifoldEKF/LieGroupEKF. For details on how static and dynamic dimensions are handled, please refer to the ManifoldEKF class documentation.
Definition at line 50 of file InvariantEKF.h.
Member Typedef Documentation
◆ Base
| using gtsam::InvariantEKF< G >::Base = LieGroupEKF<G> |
Base class type.
Definition at line 52 of file InvariantEKF.h.
◆ Covariance
| using gtsam::InvariantEKF< G >::Covariance = typename Base::Covariance |
Covariance matrix type. Eigen::Matrix<double, Dim, Dim>.
Definition at line 57 of file InvariantEKF.h.
◆ Jacobian
| using gtsam::InvariantEKF< G >::Jacobian = typename Base::Jacobian |
Jacobian for group-specific operations like AdjointMap. Eigen::Matrix<double, Dim, Dim>.
Definition at line 55 of file InvariantEKF.h.
◆ TangentVector
| using gtsam::InvariantEKF< G >::TangentVector = typename Base::TangentVector |
Tangent vector type
Definition at line 53 of file InvariantEKF.h.
Constructor & Destructor Documentation
◆ InvariantEKF()
|
inline |
Constructor: forwards to LieGroupEKF constructor.
- Parameters
-
X0 Initial state on Lie group G. P0 Initial covariance in the tangent space at X0.
Definition at line 65 of file InvariantEKF.h.
Member Function Documentation
◆ predict() [1/2]
|
inline |
Predict step via group composition (Left-Invariant): X_{k+1} = X_k * U P_{k+1} = Ad_{U^{-1}} P_k Ad_{U^{-1}}^T + Q where Ad_{U^{-1}} is the Adjoint map of U^{-1}.
- Parameters
-
U Lie group element representing the motion increment. Q Process noise covariance.
Definition at line 79 of file InvariantEKF.h.
◆ predict() [2/2]
|
inline |
Predict step via tangent control vector: U = Expmap(u * dt) Then calls predict(U, Q).
- Parameters
-
u Tangent space control vector. dt Time interval. Q Process noise covariance matrix.
Definition at line 97 of file InvariantEKF.h.
The documentation for this class was generated from the following file: