Modified DH notation robot class. More...
#include <robot.h>
Public Member Functions | |
| virtual ReturnMatrix | C (const ColumnVector &qp) |
| Joint torque due to centrifugal and Corriolis based on Recursive Newton-Euler formulation. | |
| virtual void | delta_torque (const ColumnVector &q, const ColumnVector &qp, const ColumnVector &qpp, const ColumnVector &dq, const ColumnVector &dqp, const ColumnVector &dqpp, ColumnVector &torque, ColumnVector &dtorque) |
| Delta torque dynamics. | |
| virtual void | dq_torque (const ColumnVector &q, const ColumnVector &qp, const ColumnVector &qpp, const ColumnVector &dq, ColumnVector &torque, ColumnVector &dtorque) |
| Delta torque due to delta joint position. | |
| virtual void | dqp_torque (const ColumnVector &q, const ColumnVector &qp, const ColumnVector &dqp, ColumnVector &torque, ColumnVector &dtorque) |
| Delta torque due to delta joint velocity. | |
| virtual void | dTdqi (Matrix &dRot, ColumnVector &dp, const int i) |
| Partial derivative of the robot position (homogeneous transf.) | |
| virtual ReturnMatrix | dTdqi (const int i) |
| Partial derivative of the robot position (homogeneous transf.) | |
| virtual ReturnMatrix | G () |
| Joint torque due to gravity based on Recursive Newton-Euler formulation. | |
| ReturnMatrix | inv_kin (const Matrix &Tobj, const int mj=0) |
| Overload inv_kin function. | |
| virtual ReturnMatrix | inv_kin (const Matrix &Tobj, const int mj, const int endlink, bool &converge) |
| Inverse kinematics solutions. | |
| virtual ReturnMatrix | inv_kin_puma (const Matrix &Tobj, bool &converge) |
| Analytic Puma inverse kinematics. | |
| virtual ReturnMatrix | inv_kin_rhino (const Matrix &Tobj, bool &converge) |
| Analytic Rhino inverse kinematics. | |
| virtual ReturnMatrix | inv_kin_schilling (const Matrix &Tobj, bool &converge) |
| Analytic Schilling inverse kinematics. | |
| virtual ReturnMatrix | jacobian (const int ref=0) const |
| Jacobian of mobile links expressed at frame ref. | |
| virtual ReturnMatrix | jacobian (const int endlink, const int ref) const |
| Jacobian of mobile joints up to endlink expressed at frame ref. | |
| virtual ReturnMatrix | jacobian_dot (const int ref=0) const |
| Jacobian derivative of mobile joints expressed at frame ref. | |
| virtual void | kine_pd (Matrix &Rot, ColumnVector &pos, ColumnVector &pos_dot, const int ref) const |
| Direct kinematics with velocity. | |
| mRobot (const int ndof=1) | |
| Constructor. | |
| mRobot (const Matrix &initrobot_motor) | |
| Constructor. | |
| mRobot (const Matrix &initrobot, const Matrix &initmotor) | |
| Constructor. | |
| mRobot (const mRobot &x) | |
| Copy constructor. | |
| mRobot (const std::string &filename, const std::string &robotName) | |
| virtual void | robotType_inv_kin () |
| Identify inverse kinematics familly. | |
| virtual ReturnMatrix | torque (const ColumnVector &q, const ColumnVector &qp, const ColumnVector &qpp) |
| Joint torque, without contact force, based on Recursive Newton-Euler formulation. | |
| virtual ReturnMatrix | torque (const ColumnVector &q, const ColumnVector &qp, const ColumnVector &qpp, const ColumnVector &Fext_, const ColumnVector &Next_) |
| Joint torque based on Recursive Newton-Euler formulation. | |
| virtual ReturnMatrix | torque_novelocity (const ColumnVector &qpp) |
| Joint torque. when joint velocity is 0, based on Recursive Newton-Euler formulation. | |
| virtual | ~mRobot () |
| Destructor. | |
Detailed Description
Constructor & Destructor Documentation
| mRobot::mRobot | ( | const int | ndof = 1 | ) |
| mRobot::mRobot | ( | const Matrix & | initrobot_motor | ) |
| mRobot::mRobot | ( | const Matrix & | initrobot, |
| const Matrix & | initmotor | ||
| ) |
| mRobot::mRobot | ( | const mRobot & | x | ) |
| mRobot::mRobot | ( | const std::string & | filename, |
| const std::string & | robotName | ||
| ) |
| virtual mRobot::~mRobot | ( | ) | [inline, virtual] |
Member Function Documentation
| ReturnMatrix mRobot::C | ( | const ColumnVector & | qp | ) | [virtual] |
Joint torque due to centrifugal and Corriolis based on Recursive Newton-Euler formulation.
Implements Robot_basic.
Definition at line 636 of file dynamics.cpp.
| void mRobot::delta_torque | ( | const ColumnVector & | q, |
| const ColumnVector & | qp, | ||
| const ColumnVector & | qpp, | ||
| const ColumnVector & | dq, | ||
| const ColumnVector & | dqp, | ||
| const ColumnVector & | dqpp, | ||
| ColumnVector & | ltorque, | ||
| ColumnVector & | dtorque | ||
| ) | [virtual] |
Delta torque dynamics.
This function computes
![\[ \delta \tau = D(q) \delta \ddot{q} + S_1(q,\dot{q}) \delta \dot{q} + S_2(q,\dot{q},\ddot{q}) \delta q \]](form_45.png)
Murray and Neuman Cite_: Murray86 have developed an efficient recursive linearized Newton-Euler formulation. In order to apply the RNE as presented in let us define the following variables
![\[ p_{di} = \frac{\partial p_i}{\partial d_i} = \left [ \begin{array}{ccc} 0 & \sin \alpha_i & \cos \alpha_i \end{array} \right ]^T \]](form_46.png)
![\[ Q = \left [ \begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right ] \]](form_47.png)
Forward Iterations for 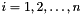 . Initialize:
. Initialize: 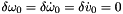 .
.
![\[ \delta \omega_i = R_i^T \delta \omega_{i-1} + \sigma_i (z_0 \delta \dot{\theta}_i - QR_i^T \omega_i \delta \theta_i) \]](form_61.png)
![\[ \delta \dot{\omega}_i = R_i^T \delta \dot{w}_{i-1} + \sigma_i [R_i^T \delta \omega_{i-1} \times z_0 \dot{\theta}_i + R_i^T \omega_{i-1} \times z_0 \delta \dot{\theta}_i + z_0 \ddot{\theta}_i - (QR_i^T \dot{\omega}_{i-1} + QR_i^T \omega_{i-1} \times \omega{z}_0 \dot{\theta}_i) \delta \theta_i ] \]](form_62.png)
![\[ \delta \dot{v}_i = R_i^T\Big(\delta \dot{\omega}_{i-1} \times p_i + \delta \omega_{i-1} \times(\omega_{i-1} \times p_i) + \omega_{i-1} \times( \delta \omega_{i-1} \times p_i) + \delta \dot{v}_i\Big) + (1-\sigma_i)\Big(2\delta \omega_i \times z_0\dot{d}_i + 2\omega_i \times z_0 \delta \dot{d}_i + z_0 \delta \ddot{d}_i\Big) - \sigma_i QR_i^T \Big(\dot{\omega}_{i-1} \times p_i + \omega_{i-1} \times(w_{i-1}\times p_i) + \dot{v}_i\Big) \delta \theta_i + (1-\sigma_i) R_i^T \Big(\dot{\omega}_{i-1} \times p_{di} + \omega_{i-1} \times(\omega_{i-1}\times p_{di})\Big) \delta d_i \]](form_63.png)
Backward Iterations for 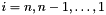 . Initialize:
. Initialize: 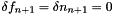 .
.
![\[ \delta \dot{v}_{ci} = \delta \dot{v}_i + \delta \dot{\omega}_i\times r_i + \delta \omega_i \times(\omega_i \times r_i) + \omega_i \times ( \delta \omega_i \times r_i) \]](form_64.png)
![\[ \delta F_i = m_i \delta \dot{v}_{ci} \]](form_56.png)
![\[ \delta N_i = I_{ci} \delta \dot{\omega}_i + \delta \omega_i \times (I_{ci}\omega_i) + \omega_i \times (I_{ci} \delta \omega_i) \]](form_65.png)
![\[ \delta f_i = R_{i+1} \delta f_{i+1} + \delta F_i + \sigma_{i+1} R_{i+1} Qf_{i+1} \delta \theta_{i+1} \]](form_66.png)
![\[ \delta n_i = \delta N_i + R_{i+1} \delta n_{i+1} + r_i\times \delta F_i + p_{i+1} \times R_{i+1} \delta f_{i+1} + \sigma_{i+1} \Big( R_{i+1} Qn_{i+1} + p_{i+1} \times R_{i+1} Qf_{i+1} \Big) \delta \theta_{i+1} + (1-\sigma_{i+1} ) p_{di+1} p_{di+1} \times R_{i+1} f_{i+1} \delta d_{i+1} \]](form_67.png)
![\[ \delta \tau_i = \sigma \delta n_i^T z_0 + (1 - \sigma_i) \delta f_i^T z_0 \]](form_68.png)
Implements Robot_basic.
Definition at line 291 of file delta_t.cpp.
| void mRobot::dq_torque | ( | const ColumnVector & | q, |
| const ColumnVector & | qp, | ||
| const ColumnVector & | qpp, | ||
| const ColumnVector & | dq, | ||
| ColumnVector & | ltorque, | ||
| ColumnVector & | dtorque | ||
| ) | [virtual] |
Delta torque due to delta joint position.
This function computes  . See mRobot::delta_torque for equations.
. See mRobot::delta_torque for equations.
Implements Robot_basic.
Definition at line 205 of file comp_dq.cpp.
| void mRobot::dqp_torque | ( | const ColumnVector & | q, |
| const ColumnVector & | qp, | ||
| const ColumnVector & | dqp, | ||
| ColumnVector & | ltorque, | ||
| ColumnVector & | dtorque | ||
| ) | [virtual] |
Delta torque due to delta joint velocity.
This function computes  . See mRobot::delta_torque for equations.
. See mRobot::delta_torque for equations.
Implements Robot_basic.
Definition at line 188 of file comp_dqp.cpp.
| void mRobot::dTdqi | ( | Matrix & | dRot, |
| ColumnVector & | dp, | ||
| const int | i | ||
| ) | [virtual] |
Partial derivative of the robot position (homogeneous transf.)
This function computes the partial derivatives:
![\[ \frac{\partial{}^0 T_n}{\partial q_i} = {}^0 T_{i} Q_i \; {}^{i} T_n \]](form_111.png)
with
![\[ Q_i = \left [ \begin{array}{cccc} 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right ] \]](form_112.png)
for a revolute joint and
![\[ Q_i = \left [ \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right ] \]](form_113.png)
for a prismatic joint.
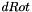 and
and 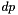 are modified on output.
are modified on output.
Implements Robot_basic.
Definition at line 582 of file kinemat.cpp.
| ReturnMatrix mRobot::dTdqi | ( | const int | i | ) | [virtual] |
Partial derivative of the robot position (homogeneous transf.)
See mRobot::dTdqi(Matrix & dRot, ColumnVector & dp, const int i) for equations.
Implements Robot_basic.
Definition at line 664 of file kinemat.cpp.
| ReturnMatrix mRobot::G | ( | ) | [virtual] |
Joint torque due to gravity based on Recursive Newton-Euler formulation.
Implements Robot_basic.
Definition at line 599 of file dynamics.cpp.
| ReturnMatrix mRobot::inv_kin | ( | const Matrix & | Tobj, |
| const int | mj = 0 |
||
| ) | [virtual] |
Overload inv_kin function.
Reimplemented from Robot_basic.
Definition at line 617 of file invkine.cpp.
| ReturnMatrix mRobot::inv_kin | ( | const Matrix & | Tobj, |
| const int | mj, | ||
| const int | endlink, | ||
| bool & | converge | ||
| ) | [virtual] |
Inverse kinematics solutions.
The solution is based on the analytic inverse kinematics if robot type (familly) is Rhino or Puma, otherwise used the numerical algoritm defined in Robot_basic class.
Reimplemented from Robot_basic.
Definition at line 625 of file invkine.cpp.
| ReturnMatrix mRobot::inv_kin_puma | ( | const Matrix & | Tobj, |
| bool & | converge | ||
| ) | [virtual] |
Analytic Puma inverse kinematics.
converge will be false if the desired end effector pose is outside robot range.
Implements Robot_basic.
Definition at line 755 of file invkine.cpp.
| ReturnMatrix mRobot::inv_kin_rhino | ( | const Matrix & | Tobj, |
| bool & | converge | ||
| ) | [virtual] |
Analytic Rhino inverse kinematics.
converge will be false if the desired end effector pose is outside robot range.
Implements Robot_basic.
Definition at line 650 of file invkine.cpp.
| ReturnMatrix mRobot::inv_kin_schilling | ( | const Matrix & | Tobj, |
| bool & | converge | ||
| ) | [virtual] |
Analytic Schilling inverse kinematics.
converge will be false if the desired end effector pose is outside robot range.
Implements Robot_basic.
Definition at line 915 of file invkine.cpp.
| virtual ReturnMatrix mRobot::jacobian | ( | const int | ref = 0 | ) | const [inline, virtual] |
Jacobian of mobile links expressed at frame ref.
Reimplemented from Robot_basic.
| ReturnMatrix mRobot::jacobian | ( | const int | endlink, |
| const int | ref | ||
| ) | const [virtual] |
Jacobian of mobile joints up to endlink expressed at frame ref.
See Robot::jacobian for equations.
Implements Robot_basic.
Definition at line 682 of file kinemat.cpp.
| ReturnMatrix mRobot::jacobian_dot | ( | const int | ref = 0 | ) | const [virtual] |
Jacobian derivative of mobile joints expressed at frame ref.
See Robot::jacobian_dot for equations.
Implements Robot_basic.
Definition at line 736 of file kinemat.cpp.
| void mRobot::kine_pd | ( | Matrix & | Rot, |
| ColumnVector & | pos, | ||
| ColumnVector & | pos_dot, | ||
| const int | j | ||
| ) | const [virtual] |
Direct kinematics with velocity.
- Parameters:
-
Rot,: Frame j rotation matrix w.r.t to the base frame. pos,: Frame j position vector wr.r.t to the base frame. pos_dot,: Frame j velocity vector w.r.t to the base frame. j,: Frame j. Print an error on the console if j is out of range.
Implements Robot_basic.
Definition at line 552 of file kinemat.cpp.
| void mRobot::robotType_inv_kin | ( | ) | [virtual] |
Identify inverse kinematics familly.
Identify the inverse kinematics analytic solution based on the similarity of the robot DH parameters and the DH parameters of know robots (ex: Puma, Rhino, ...). The inverse kinematics will be based on a numerical alogorithm if there is no match .
Implements Robot_basic.
| ReturnMatrix mRobot::torque | ( | const ColumnVector & | q, |
| const ColumnVector & | qp, | ||
| const ColumnVector & | qpp | ||
| ) | [virtual] |
Joint torque, without contact force, based on Recursive Newton-Euler formulation.
Implements Robot_basic.
Definition at line 412 of file dynamics.cpp.
| ReturnMatrix mRobot::torque | ( | const ColumnVector & | q, |
| const ColumnVector & | qp, | ||
| const ColumnVector & | qpp, | ||
| const ColumnVector & | Fext_, | ||
| const ColumnVector & | Next_ | ||
| ) | [virtual] |
Joint torque based on Recursive Newton-Euler formulation.
In order to apply the RNE, let us define the following variables (referenced in the 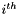 coordinate frame if applicable):
coordinate frame if applicable):
 is the joint type;
is the joint type; 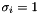 for a revolute joint and
for a revolute joint and 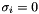 for a prismatic joint.
for a prismatic joint.
![$ z_0 = \left [ \begin{array}{ccc} 0 & 0 & 1 \end{array} \right ]^T$](form_74.png)
![$p_i = \left [ \begin{array}{ccc} a_{i-1} & -d_i sin \alpha_{i-1} & d_i cos \alpha_{i-1} \end{array} \right ]^T$](form_88.png) is the position of the $i^{th}$ with respect to the $i-1^{th}$ frame.
is the position of the $i^{th}$ with respect to the $i-1^{th}$ frame.
Forward Iterations for 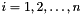 . Initialize:
. Initialize: 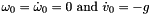 .
.
![\[ \omega_i = R_i^T\omega_{i-1} + \sigma_i z_0\dot{\theta_i} \]](form_90.png)
![\[ \dot{\omega}_i = R_i^T\dot{\omega}_{i-1} + \sigma_i R_i^T\omega_{i-1}\times z_0 \dot{\theta}_i + \sigma_iz_0\ddot{\theta}_i \]](form_91.png)
![\[ \dot{v}_i = R_i^T(\dot{\omega}_{i-1}\times p_i + \omega_{i-1}\times(\omega_{i-1}\times p_i) + \dot{v}_{i-1}) + (1 - \sigma_i)(2\omega_i\times z_0 dot{d}_i + z_0\ddot{d}_i) \]](form_92.png)
Backward Iterations for 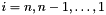 . Initialize:
. Initialize: 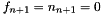 .
.
![\[ \dot{v}_{ci} = \dot{\omega}_i\times r_i + \omega_i\times(\omega_i\times r_i) + v_i \]](form_94.png)
![\[ F_i = m_i \dot{v}_{ci} \]](form_83.png)
![\[ N_i = I_{ci}\ddot{\omega}_i\ + \omega_i \times I_{ci}\omega_i \]](form_95.png)
![\[ f_i = R_{i+1}f_{i+1} + F_i \]](form_96.png)
![\[ n_i = N_i + R_{i+1} n_{i+1} + r_i \times F_i + p_{i+1}\times R_{i+1}f_{i+1} \]](form_97.png)
![\[ \tau_i = \sigma_i n_i^T z_0 + (1 - \sigma_i) f_i^T z_0 \]](form_98.png)
Implements Robot_basic.
Definition at line 422 of file dynamics.cpp.
| ReturnMatrix mRobot::torque_novelocity | ( | const ColumnVector & | qpp | ) | [virtual] |
Joint torque. when joint velocity is 0, based on Recursive Newton-Euler formulation.
Implements Robot_basic.
Definition at line 555 of file dynamics.cpp.
The documentation for this class was generated from the following files: