The elements to formulate the solver independent optimization problem. More...
Classes | |
| class | ifopt::ConstraintSet |
| A container holding a set of related constraints. More... | |
| class | ifopt::CostTerm |
| A container holding a single cost term. More... | |
| class | ifopt::Problem |
| A generic optimization problem with variables, costs and constraints. More... | |
| class | ifopt::VariableSet |
| A container holding a set of related optimization variables. More... | |
Detailed Description
The elements to formulate the solver independent optimization problem.
An optimization problem usually consists of multiple sets of independent variable- or constraint-sets. Each set represents a common concept, e.g. one set of variables represents spline coefficients, another footstep positions. Similarly, each constraint-set groups a set of similar constraints.
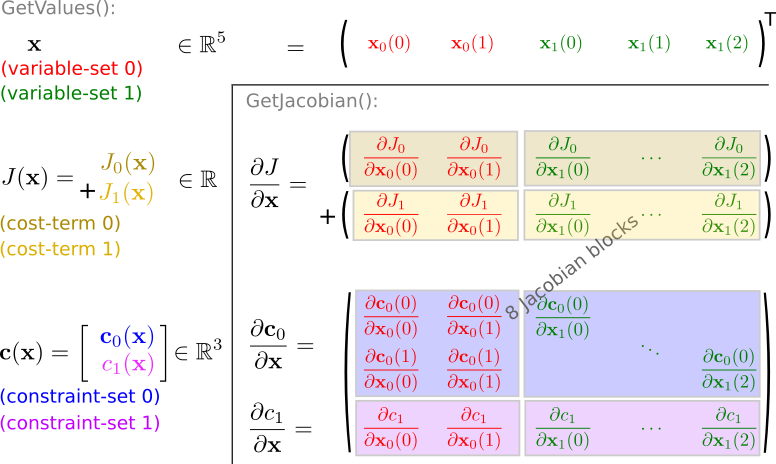
The Nonlinear Optimization Problem to solve is defined as:
find x0, x1 (variable-sets 0 & 1) s.t x0_lower <= x0 <= x0_upper (bounds on variable-set x0 R^2)
{x0,x1} = arg min c0(x0,x1)+c1(x0,x1) (cost-terms 0 and 1)
g0_lower < g0(x0,x1) < g0_upper (constraint-set 0 R^2) g1_lower < g1(x0,x1) < g0_upper (constraint-set 1 R^1)
#### GetValues() This structure allows a user to define each of these sets independently in separate classes and ifopt takes care of building the overall problem from these sets. This is implemented by * stacking all variable-sets to build the overall variable vector * summing all cost-terms to calculate the total cost * stacking all constraint-sets to build the overall constraint vector.
#### GetJacobian() Supplying derivative information greatly increases solution speed. ifopt allows to define the derivative of each cost-term/constraint-set with respect to each variable-set independently. This ensures that when the order of variable-sets changes in the overall vector, this derivative information is still valid. These "Jacobian blocks" must be supplied through ConstraintSet::FillJacobianBlock() and are then used to build the complete Jacobian for the cost and constraints.