acado: A Tutorial for the EllipsoidalIntegrator

This tutorial explains how to setup a simple simulation of an ODE system with interval valued initial value and/or parameters. The code computes an enclosure of the corresponding reachable set of the ODE.

Mathematical Formulation of the Set Propagation Problem:

We consider a simple, possibly non-linear differential equation system of the form

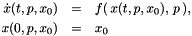
$\begin{eqnarray*} \dot x(t,p,x_0) &=& f(\,x(t,p,x_0),\,p\,),\\ x(0,p,x_0) &=& x_0 \end{eqnarray*}$

Here, the function f is a possibly nonlinear right-hand side function. Notice that the solution trajectory x(t,p,x_0) can be regarded as a function of the input variables x_0 and p. The aim of a validated integrator is to find a set Y(t) that contains the set of reachable states such that

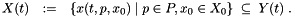
$\begin{eqnarray*} X(t) &:=& \{ x(t,p,x_0) \mid p \in P , x_0 \in X_0 \} \; \subseteq \; Y(t) \; . \end{eqnarray*}$

Here, X_0 and P are assumed to be given sets that contain the initial value and parameter, respectively.

Implementation of the Set Propagation Problem

The following piece of code shows how to implement the above set valued simulation problem:

#include <acado/validated_integrator/ellipsoidal_integrator.hpp>

USING_NAMESPACE_ACADO
    
typedef Tmatrix<Interval> IntervalVector;

int main( ){

    // DEFINE VARIABLES:
    // ----------------------
        DifferentialState      x,y;
        Parameter                p; 
        DifferentialEquation     f;
        
        f << dot(x) == p*x*(1.0-y);
        f << dot(y) == p*y*(x-1.0);

        IntervalVector x_init(2);
        x_init(0) = 1.2;
        x_init(1) = 1.1;
        
        IntervalVector p_init(1);
        p_init(0) = Interval(2.95,3.05);
        
        EllipsoidalIntegrator integrator( f, 5 );

        integrator.set(INTEGRATOR_PRINTLEVEL   , MEDIUM );
        integrator.set(INTEGRATOR_TOLERANCE    , 1e-6   );
        integrator.set(ABSOLUTE_TOLERANCE      , 1e-6   );
        
        integrator.integrate( 0.0, 8.0, 4, &x_init, &p_init );
    return 0;
}

This code example is also coming with the ACADO Toolkit and can in this version directly be compiled. The translation of the mathematical formulation into the C++ code should be intuitive. Notice that the constructor of the class "EllipsoidalIntegrator" takes the right-hand side function as well as the order of the time series expansion as arguments. The arguments of the function integrate(...) specify the time horizon (start and end time) followed by the order of the Taylor model and the inputs for the initial states and parameters.

A brief discussion of the results

Compiling and running the code should lead to both: An output of the integrator should be an interval that contains the solution for the state trajectory at time T = 8. The result looks as follows:

time = 8.000000e+00 

STATE ENCLOSURE: 

x[0]:  [ 1.070966e+00 : 1.212944e+00 ]
x[1]:  [ 8.130292e-01 : 9.203568e-01 ]

Here, the state enclosure for the first and second component of the state are printed in form of intervals at the end time T = 8.0.