TooN::WLS< Size, Precision, Decomposition > Class Template Reference
[Linear equation solvers]

#include <wls.h>

List of all members.

Public Member Functions

template<int N, class B1 , class B2 , class B3 >
void add_mJ (const Vector< N, Precision, B1 > &m, const Matrix< Size, N, Precision, B2 > &J, const Matrix< N, N, Precision, B3 > &invcov)
template<class B2 >
void add_mJ (Precision m, const Vector< Size, Precision, B2 > &J, Precision weight=1)
template<class B2 >
void add_prior (const Matrix< Size, Size, Precision, B2 > &m)
template<class B2 >
void add_prior (const Vector< Size, Precision, B2 > &v)
void add_prior (Precision val)
void clear ()
 Clear all the measurements and apply a constant regularisation term.
void compute ()
const Matrix< Size, Size,
Precision > & 		get_C_inv () const
 Returns the inverse covariance matrix.
Matrix< Size, Size, Precision > & get_C_inv ()
 Returns the inverse covariance matrix.
const Decomposition< Size,
Precision > & 		get_decomposition () const
 Return the decomposition object used to compute 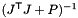$(J^{\mathsf T} J + P)^{-1}$.
Decomposition< Size, Precision > & get_decomposition ()
 Return the decomposition object used to compute 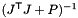$(J^{\mathsf T} J + P)^{-1}$.
const Vector< Size, Precision > & get_mu () const
 Returns the update. With no prior, this is the result of 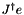$J^\dagger e$.
Vector< Size, Precision > & get_mu ()
 Returns the update. With no prior, this is the result of 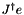$J^\dagger e$.
const Vector< Size, Precision > & get_vector () const
 Returns the vector 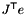$J^{\mathsf T} e$.
Vector< Size, Precision > & get_vector ()
 Returns the vector 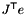$J^{\mathsf T} e$.
void operator+= (const WLS &meas)
 WLS (int size=0)
 Default constructor or construct with the number of dimensions for the Dynamic case.

Private Member Functions

int operator= (WLS &copyof)
 WLS (WLS &copyof)

Private Attributes

Matrix< Size, Size, Precision > my_C_inv
Decomposition< Size, Precision > my_decomposition
Vector< Size, Precision > my_mu
Vector< Size, Precision > my_vector

Detailed Description

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
class TooN::WLS< Size, Precision, Decomposition >

Performs Gauss-Newton weighted least squares computation.

Parameters:
Size The number of dimensions in the system
Precision The numerical precision used (double, float etc)
Decomposition The class used to invert the inverse Covariance matrix (must have one integer size and one typename precision template arguments) this is Cholesky by default, but could also be SQSVD

Definition at line 48 of file wls.h.

Constructor & Destructor Documentation

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
TooN::WLS< Size, Precision, Decomposition >::WLS ( int  size = 0  )  [inline]

Default constructor or construct with the number of dimensions for the Dynamic case.

Definition at line 52 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
TooN::WLS< Size, Precision, Decomposition >::WLS ( WLS< Size, Precision, Decomposition > &  copyof  )  [private]

Member Function Documentation

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
template<int N, class B1 , class B2 , class B3 >
void TooN::WLS< Size, Precision, Decomposition >::add_mJ ( const Vector< N, Precision, B1 > &  m,
const Matrix< Size, N, Precision, B2 > &  J,
const Matrix< N, N, Precision, B3 > &  invcov 
) [inline]

Add multiple measurements at once (much more efficiently)

Parameters:
m The measurements to add
J The Jacobian matrix 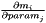$\frac{\partial\text{m}_i}{\partial\text{param}_j}$
invcov The inverse covariance of the measurement values

Definition at line 117 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
template<class B2 >
void TooN::WLS< Size, Precision, Decomposition >::add_mJ ( Precision  m,
const Vector< Size, Precision, B2 > &  J,
Precision  weight = 1 
) [inline]

Add a single measurement

Parameters:
m The value of the measurement
J The Jacobian for the measurement $\frac{\partial\text{m}}{\partial\text{param}_i}$
weight The inverse variance of the measurement (default = 1)

Definition at line 100 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
template<class B2 >
void TooN::WLS< Size, Precision, Decomposition >::add_prior ( const Matrix< Size, Size, Precision, B2 > &  m  )  [inline]

Applies a whole-matrix regularisation term. This is the same as adding the 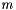$m$ to the inverse covariance matrix.

Parameters:
m The inverse covariance matrix to add

Definition at line 91 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
template<class B2 >
void TooN::WLS< Size, Precision, Decomposition >::add_prior ( const Vector< Size, Precision, B2 > &  v  )  [inline]

Applies a regularisation term with a different strength for each parameter value. Equates to a prior that says all the parameters are zero with 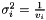$\sigma_i^2 = \frac{1}{\text{v}_i}$.

Parameters:
v The vector of priors

Definition at line 80 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
void TooN::WLS< Size, Precision, Decomposition >::add_prior ( Precision  val  )  [inline]

Applies a constant regularisation term. Equates to a prior that says all the parameters are zero with 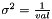$\sigma^2 = \frac{1}{\text{val}}$.

Parameters:
val The strength of the prior

Definition at line 70 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
void TooN::WLS< Size, Precision, Decomposition >::clear (  )  [inline]

Clear all the measurements and apply a constant regularisation term.

Reimplemented in TooN::IRLS< Size, Precision, Reweight >.

Definition at line 62 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
void TooN::WLS< Size, Precision, Decomposition >::compute (  )  [inline]

Process all the measurements and compute the weighted least squares set of parameter values stores the result internally which can then be accessed by calling get_mu()

Definition at line 128 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
const Matrix<Size,Size,Precision>& TooN::WLS< Size, Precision, Decomposition >::get_C_inv (  )  const [inline]

Returns the inverse covariance matrix.

Definition at line 149 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
Matrix<Size,Size,Precision>& TooN::WLS< Size, Precision, Decomposition >::get_C_inv (  )  [inline]

Returns the inverse covariance matrix.

Definition at line 147 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
const Decomposition<Size,Precision>& TooN::WLS< Size, Precision, Decomposition >::get_decomposition (  )  const [inline]

Return the decomposition object used to compute 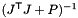$(J^{\mathsf T} J + P)^{-1}$.

Definition at line 155 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
Decomposition<Size,Precision>& TooN::WLS< Size, Precision, Decomposition >::get_decomposition (  )  [inline]

Return the decomposition object used to compute $(J^{\mathsf T} J + P)^{-1}$.

Definition at line 154 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
const Vector<Size,Precision>& TooN::WLS< Size, Precision, Decomposition >::get_mu (  )  const [inline]

Returns the update. With no prior, this is the result of 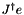$J^\dagger e$.

Definition at line 151 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
Vector<Size,Precision>& TooN::WLS< Size, Precision, Decomposition >::get_mu (  )  [inline]

Returns the update. With no prior, this is the result of 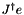$J^\dagger e$.

Definition at line 150 of file wls.h.

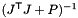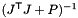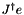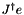template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
const Vector<Size,Precision>& TooN::WLS< Size, Precision, Decomposition >::get_vector (  )  const [inline]

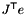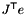Returns the vector $J^{\mathsf T} e$.

Definition at line 153 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
Vector<Size,Precision>& TooN::WLS< Size, Precision, Decomposition >::get_vector (  )  [inline]

Returns the vector $J^{\mathsf T} e$.

Definition at line 152 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
void TooN::WLS< Size, Precision, Decomposition >::operator+= ( const WLS< Size, Precision, Decomposition > &  meas  )  [inline]

Combine measurements from two WLS systems

Parameters:
meas The measurements to combine with

Definition at line 141 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
int TooN::WLS< Size, Precision, Decomposition >::operator= ( WLS< Size, Precision, Decomposition > &  copyof  )  [private]

Member Data Documentation

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
Matrix<Size,Size,Precision> TooN::WLS< Size, Precision, Decomposition >::my_C_inv [private]

Definition at line 159 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
Decomposition<Size,Precision> TooN::WLS< Size, Precision, Decomposition >::my_decomposition [private]

Definition at line 161 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
Vector<Size,Precision> TooN::WLS< Size, Precision, Decomposition >::my_mu [private]

Definition at line 162 of file wls.h.

template<int Size = Dynamic, class Precision = double, template< int Size, class Precision > class Decomposition = Cholesky>
Vector<Size,Precision> TooN::WLS< Size, Precision, Decomposition >::my_vector [private]

Definition at line 160 of file wls.h.

The documentation for this class was generated from the following file:
 All Classes Namespaces Files Functions Variables Typedefs Friends Defines

libtoon
Author(s): Florian Weisshardt
autogenerated on Fri Jan 11 10:09:50 2013