TooN::SO3< Precision > Class Template Reference
[Transformation matrices]

#include <so3.h>

List of all members.

Classes

struct  Invert

Public Member Functions

template<int S, typename A >
Vector< 3, Precision > adjoint (const Vector< S, Precision, A > &vect) const
void coerce ()
 Modifies the matrix to make sure it is a valid rotation matrix.
template<int S, typename VP , typename VA >
SO3< Precision > exp (const Vector< S, VP, VA > &w)
const Matrix< 3, 3, Precision > & get_matrix () const
 Returns the SO3 as a Matrix<3>
SO3 inverse () const
 Returns the inverse of this matrix (=the transpose, so this is a fast operation).
Vector< 3, Precision > ln () const
SO3 operator* (const SO3 &rhs) const
 Right-multiply by another rotation matrix.
SO3 & operator*= (const SO3 &rhs)
 Right-multiply by another rotation matrix.
template<int R, int C, typename P , typename A >
SO3 & operator= (const Matrix< R, C, P, A > &rhs)
template<int S1, int S2, typename P1 , typename P2 , typename A1 , typename A2 >
 SO3 (const Vector< S1, P1, A1 > &a, const Vector< S2, P2, A2 > &b)
template<int R, int C, typename P , typename A >
 SO3 (const Matrix< R, C, P, A > &rhs)
 Construct from a rotation matrix.
template<int S, typename P , typename A >
 SO3 (const Vector< S, P, A > &v)
 Construct from the axis of rotation (and angle given by the magnitude).
 SO3 ()
 Default constructor. Initialises the matrix to the identity (no rotation).

Static Public Member Functions

template<int S, typename VP , typename A >
static SO3 exp (const Vector< S, VP, A > &vect)
static Matrix< 3, 3, Precision > generator (int i)
template<typename Base >
static Vector< 3, Precision > generator_field (int i, const Vector< 3, Precision, Base > &pos)
 Returns the i-th generator times pos.

Private Member Functions

 SO3 (const SO3 &a, const SO3 &b)
 SO3 (const SO3 &so3, const Invert &)

Private Attributes

Matrix< 3, 3, Precision > my_matrix

Friends

std::istream & operator>> (std::istream &is, SE3< Precision > &rhs)
std::istream & operator>> (std::istream &is, SO3< Precision > &rhs)
class SE3< Precision >

Related Functions

(Note that these are not member functions.)



template<int R, int C, typename P , typename PM , typename A >
Matrix< R, 3, typename
Internal::MultiplyType< PM, P >
::type > 		operator* (const Matrix< R, C, PM, A > &lhs, const SO3< P > &rhs)
template<int R, int C, typename P , typename PM , typename A >
Matrix< 3, C, typename
Internal::MultiplyType< P, PM >
::type > 		operator* (const SO3< P > &lhs, const Matrix< R, C, PM, A > &rhs)
template<int S, typename P , typename PV , typename A >
Vector< 3, typename
Internal::MultiplyType< PV, P >
::type > 		operator* (const Vector< S, PV, A > &lhs, const SO3< P > &rhs)
template<int S, typename P , typename PV , typename A >
Vector< 3, typename
Internal::MultiplyType< P, PV >
::type > 		operator* (const SO3< P > &lhs, const Vector< S, PV, A > &rhs)
template<typename Precision >
std::ostream & operator<< (std::ostream &os, const SO3< Precision > &rhs)
template<typename Precision , typename VP , typename VA , typename MA >
void rodrigues_so3_exp (const Vector< 3, VP, VA > &w, const Precision A, const Precision B, Matrix< 3, 3, Precision, MA > &R)

Detailed Description

template<typename Precision = double>
class TooN::SO3< Precision >

Class to represent a three-dimensional rotation matrix. Three-dimensional rotation matrices are members of the Special Orthogonal Lie group SO3. This group can be parameterised three numbers (a vector in the space of the Lie Algebra). In this class, the three parameters are the finite rotation vector, i.e. a three-dimensional vector whose direction is the axis of rotation and whose length is the angle of rotation in radians. Exponentiating this vector gives the matrix, and the logarithm of the matrix gives this vector.

Definition at line 53 of file so3.h.

Constructor & Destructor Documentation

template<typename Precision = double>
TooN::SO3< Precision >::SO3 (  )  [inline]

Default constructor. Initialises the matrix to the identity (no rotation).

Definition at line 60 of file so3.h.

template<typename Precision = double>
template<int S, typename P , typename A >
TooN::SO3< Precision >::SO3 ( const Vector< S, P, A > &  v  )  [inline]

Construct from the axis of rotation (and angle given by the magnitude).

Definition at line 64 of file so3.h.

template<typename Precision = double>
template<int R, int C, typename P , typename A >
TooN::SO3< Precision >::SO3 ( const Matrix< R, C, P, A > &  rhs  )  [inline]

Construct from a rotation matrix.

Definition at line 68 of file so3.h.

template<typename Precision = double>
template<int S1, int S2, typename P1 , typename P2 , typename A1 , typename A2 >
TooN::SO3< Precision >::SO3 ( const Vector< S1, P1, A1 > &  a,
const Vector< S2, P2, A2 > &  b 
) [inline]

creates an SO3 as a rotation that takes Vector a into the direction of Vector b with the rotation axis along a ^ b. If |a ^ b| == 0, it creates the identity rotation. An assertion will fail if Vector a and Vector b are in exactly opposite directions.

Parameters:
a source Vector
b target Vector

Definition at line 76 of file so3.h.

template<typename Precision = double>
TooN::SO3< Precision >::SO3 ( const SO3< Precision > &  so3,
const Invert &   
) [inline, private]

Definition at line 177 of file so3.h.

template<typename Precision = double>
TooN::SO3< Precision >::SO3 ( const SO3< Precision > &  a,
const SO3< Precision > &  b 
) [inline, private]

Definition at line 178 of file so3.h.

Member Function Documentation

template<typename Precision = double>
template<int S, typename A >
Vector<3, Precision> TooN::SO3< Precision >::adjoint ( const Vector< S, Precision, A > &  vect  )  const [inline]

Transfer a vector in the Lie Algebra from one co-ordinate frame to another such that for a matrix $ M $, the adjoint $Adj()$ obeys $ e^{\text{Adj}(v)} = Me^{v}M^{-1} $

Definition at line 169 of file so3.h.

template<typename Precision = double>
void TooN::SO3< Precision >::coerce (  )  [inline]

Modifies the matrix to make sure it is a valid rotation matrix.

Definition at line 108 of file so3.h.

template<typename Precision = double>
template<int S, typename VP , typename VA >
SO3<Precision> TooN::SO3< Precision >::exp ( const Vector< S, VP, VA > &  w  )  [inline]

Perform the exponential of the matrix $ \sum_i w_iG_i$

Parameters:
w Weightings of the generator matrices.

Definition at line 244 of file so3.h.

template<typename Precision = double>
template<int S, typename VP , typename A >
static SO3 TooN::SO3< Precision >::exp ( const Vector< S, VP, A > &  vect  )  [inline, static]

Exponentiate a vector in the Lie algebra to generate a new SO3. See the Detailed Description for details of this vector.

template<typename Precision = double>
static Matrix<3,3, Precision> TooN::SO3< Precision >::generator ( int  i  )  [inline, static]

Returns the i-th generator. The generators of a Lie group are the basis for the space of the Lie algebra. For SO3, the generators are three $3\times3$ matrices representing the three possible (linearised) rotations.

Definition at line 146 of file so3.h.

template<typename Precision = double>
template<typename Base >
static Vector<3,Precision> TooN::SO3< Precision >::generator_field ( int  i,
const Vector< 3, Precision, Base > &  pos 
) [inline, static]

Returns the i-th generator times pos.

Definition at line 155 of file so3.h.

template<typename Precision = double>
const Matrix<3,3, Precision>& TooN::SO3< Precision >::get_matrix (  )  const [inline]

Returns the SO3 as a Matrix<3>

Definition at line 140 of file so3.h.

template<typename Precision = double>
SO3 TooN::SO3< Precision >::inverse (  )  const [inline]

Returns the inverse of this matrix (=the transpose, so this is a fast operation).

Definition at line 128 of file so3.h.

template<typename Precision >
Vector< 3, Precision > TooN::SO3< Precision >::ln (  )  const [inline]

Take the logarithm of the matrix, generating the corresponding vector in the Lie Algebra. See the Detailed Description for details of this vector.

Definition at line 278 of file so3.h.

template<typename Precision = double>
SO3 TooN::SO3< Precision >::operator* ( const SO3< Precision > &  rhs  )  const [inline]

Right-multiply by another rotation matrix.

Definition at line 137 of file so3.h.

template<typename Precision = double>
SO3& TooN::SO3< Precision >::operator*= ( const SO3< Precision > &  rhs  )  [inline]

Right-multiply by another rotation matrix.

Definition at line 131 of file so3.h.

template<typename Precision = double>
template<int R, int C, typename P , typename A >
SO3& TooN::SO3< Precision >::operator= ( const Matrix< R, C, P, A > &  rhs  )  [inline]

Assigment operator from a general matrix. This also calls coerce() to make sure that the matrix is a valid rotation matrix.

Definition at line 101 of file so3.h.

Friends And Related Function Documentation

template<int R, int C, typename P , typename PM , typename A >
Matrix< R, 3, typename Internal::MultiplyType< PM, P >::type > operator* ( const Matrix< R, C, PM, A > &  lhs,
const SO3< P > &  rhs 
) [related]

Left-multiply by a matrix

Definition at line 347 of file so3.h.

template<int R, int C, typename P , typename PM , typename A >
Matrix< 3, C, typename Internal::MultiplyType< P, PM >::type > operator* ( const SO3< P > &  lhs,
const Matrix< R, C, PM, A > &  rhs 
) [related]

Right-multiply by a matrix

Definition at line 340 of file so3.h.

template<int S, typename P , typename PV , typename A >
Vector< 3, typename Internal::MultiplyType< PV, P >::type > operator* ( const Vector< S, PV, A > &  lhs,
const SO3< P > &  rhs 
) [related]

Left-multiply by a Vector

Definition at line 333 of file so3.h.

template<int S, typename P , typename PV , typename A >
Vector< 3, typename Internal::MultiplyType< P, PV >::type > operator* ( const SO3< P > &  lhs,
const Vector< S, PV, A > &  rhs 
) [related]

Right-multiply by a Vector

Definition at line 326 of file so3.h.

template<typename Precision >
std::ostream & operator<< ( std::ostream &  os,
const SO3< Precision > &  rhs 
) [related]

Write an SO3 to a stream

Definition at line 186 of file so3.h.

template<typename Precision = double>
std::istream & operator>> ( std::istream &  is,
SE3< Precision > &  rhs 
) [friend]

Reads an SE3 from a stream

Definition at line 234 of file se3.h.

template<typename Precision = double>
std::istream & operator>> ( std::istream &  is,
SO3< Precision > &  rhs 
) [friend]

Read from SO3 to a stream

Definition at line 193 of file so3.h.

template<typename Precision , typename VP , typename VA , typename MA >
void rodrigues_so3_exp ( const Vector< 3, VP, VA > &  w,
const Precision  A,
const Precision  B,
Matrix< 3, 3, Precision, MA > &  R 
) [related]

Compute a rotation exponential using the Rodrigues Formula. The rotation axis is given by 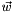$\vec{w}$, and the rotation angle must be computed using 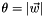$ \theta = |\vec{w}|$. This is provided as a separate function primarily to allow fast and rough matrix exponentials using fast and rough approximations to A and B.

Parameters:
w Vector about which to rotate.
A $\frac{\sin \theta}{\theta}$
B $\frac{1 - \cos \theta}{\theta^2}$
R Matrix to hold the return value.

Definition at line 210 of file so3.h.

template<typename Precision = double>
friend class SE3< Precision > [friend]

Definition at line 57 of file so3.h.

Member Data Documentation

template<typename Precision = double>
Matrix<3,3, Precision> TooN::SO3< Precision >::my_matrix [private]

Definition at line 180 of file so3.h.

The documentation for this class was generated from the following files:
 All Classes Namespaces Files Functions Variables Typedefs Friends Defines

libtoon
Author(s): Florian Weisshardt
autogenerated on Fri Jan 11 10:09:50 2013