TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V > Class Template Reference
[Matrix decompositions]
#include <GR_SVD.h>
List of all members.
Public Member Functions |
| template<int Size, typename P2 , typename B2 > |
Vector< N, typename
Internal::MultiplyType
< Precision, P2 >::type > | backsub (const Vector< Size, P2, B2 > &rhs, const Precision condition=1e9) |
| template<int Rows2, int Cols2, typename P2 , typename B2 > |
Matrix< N, Cols2, typename
Internal::MultiplyType
< Precision, P2 >::type > | backsub (const Matrix< Rows2, Cols2, P2, B2 > &rhs, const Precision condition=1e9) |
| const Vector< N, Precision > & | get_diagonal () |
| void | get_inv_diag (Vector< N > &inv_diag, const Precision condition) |
| Precision | get_largest_singular_value () |
| Matrix< N, M, Precision > | get_pinv (const Precision condition=1e9) |
| | Get the pseudo-inverse  .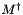
|
| Precision | get_smallest_singular_value () |
| int | get_smallest_singular_value_index () |
| const Matrix< M, N, Precision > & | get_U () |
| const Matrix< N, N, Precision > & | get_V () |
| template<class Precision2 , class Base > |
| | GR_SVD (const Matrix< M, N, Precision2, Base > &A) |
| void | reorder () |
| | Reorder the components so the singular values are in descending order.
|
Static Public Attributes |
| static const int | BigDim = M>N?M:N |
| static const int | SmallDim = M<N?M:N |
Protected Member Functions |
| void | Accumulate_LHS () |
| void | Accumulate_RHS () |
| void | Bidiagonalize () |
| void | Diagonalize () |
| bool | Diagonalize_SubLoop (int k, Precision &z) |
Protected Attributes |
| Precision | anorm |
| Matrix< M, N, Precision > | mU |
| Matrix< N, N, Precision > | mV |
| int | nError |
| int | nIterations |
| Vector< N, Precision > | vDiagonal |
| Vector< BigDim, Precision > | vOffDiagonal |
Detailed Description
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
class TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >
Performs SVD and back substitute to solve equations. This code is a c++ translation of the FORTRAN routine give in George E. Forsythe et al, Computer Methods for Mathematical Computations, Prentice-Hall 1977. That code itself is a translation of the ALGOL routine by Golub and Reinsch, Num. Math. 14, 403-420, 1970.
N.b. the singular values returned by this routine are not sorted. N.b. this also means that even for MxN matrices with M<N, N singular values are computed and used.
The template parameters WANT_U and WANT_V may be set to false to indicate that U and/or V are not needed for a minor speed-up.
Definition at line 60 of file GR_SVD.h.
Constructor & Destructor Documentation
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
template<class Precision2 , class Base >
Member Function Documentation
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
| void TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::Accumulate_LHS |
( |
|
) |
[inline, protected] |
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
| void TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::Accumulate_RHS |
( |
|
) |
[inline, protected] |
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int Size, typename P2 , typename B2 >
Calculate result of multiplying the (pseudo-)inverse of M by a vector. For a vector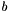 
, this calculates 
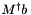by back substitution (i.e. without explictly calculating the (pseudo-)inverse). See the detailed description for a description of condition variables.
Definition at line 109 of file GR_SVD.h.
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int Rows2, int Cols2, typename P2 , typename B2 >
| Matrix<N,Cols2, typename Internal::MultiplyType<Precision,P2>::type > TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::backsub |
( |
const Matrix< Rows2, Cols2, P2, B2 > & |
rhs, |
|
|
const Precision |
condition = 1e9 | |
|
) |
| | [inline] |
Calculate result of multiplying the (pseudo-)inverse of M by another matrix. For a matrix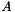 
, this calculates 
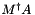by back substitution (i.e. without explictly calculating the (pseudo-)inverse). See the detailed description for a description of condition variables.
Definition at line 96 of file GR_SVD.h.
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
| void TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::Bidiagonalize |
( |
|
) |
[inline, protected] |
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
| void TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::Diagonalize |
( |
|
) |
[inline, protected] |
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
| bool TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::Diagonalize_SubLoop |
( |
int |
k, |
|
|
Precision & |
z | |
|
) |
| | [inline, protected] |
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
| const Vector<N, Precision>& TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::get_diagonal |
( |
|
) |
[inline] |
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
| void TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::get_inv_diag |
( |
Vector< N > & |
inv_diag, |
|
|
const Precision |
condition | |
|
) |
| | [inline] |
Return the pesudo-inverse diagonal. The reciprocal of the diagonal elements is returned if the elements are well scaled with respect to the largest element, otherwise 0 is returned.
- Parameters:
-
| inv_diag | Vector in which to return the inverse diagonal. |
| condition | Elements must be larger than this factor times the largest diagonal element to be considered well scaled. |
Definition at line 82 of file GR_SVD.h.
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
| Precision TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::get_largest_singular_value |
( |
|
) |
[inline] |
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
| Matrix<N,M,Precision> TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::get_pinv |
( |
const Precision |
condition = 1e9 |
) |
[inline] |
Get the pseudo-inverse .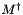
Definition at line 117 of file GR_SVD.h.
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
| Precision TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::get_smallest_singular_value |
( |
|
) |
[inline] |
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
| int TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::get_smallest_singular_value_index |
( |
|
) |
[inline] |
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
| const Matrix<M,N,Precision>& TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::get_U |
( |
|
) |
[inline] |
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
| const Matrix<N,N,Precision>& TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::get_V |
( |
|
) |
[inline] |
template<int M, int N, class Precision , bool WANT_U, bool WANT_V>
| void TooN::GR_SVD< M, N, Precision, WANT_U, WANT_V >::reorder |
( |
|
) |
[inline] |
Reorder the components so the singular values are in descending order.
Definition at line 494 of file GR_SVD.h.
Member Data Documentation
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
template<int M, int N, class Precision = DefaultPrecision, bool WANT_U = 1, bool WANT_V = 1>
The documentation for this class was generated from the following file:
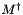