acado: Code Generation Tool: auto generated integrators

Here is going to be described, in details, how to setup a simple example and to generate optimized code for and NMPC application using the ACADO Code Generation Tool (CGT). We also sketch how to run the generated code.

For an MHE and more challenging examples, please study the examples in the examples/code_generation/mhe_mpc folder. There you can also find examples for Matlab MEX and Simulink interfaces.

A Tutorial Example

Illustration of an overhead crane

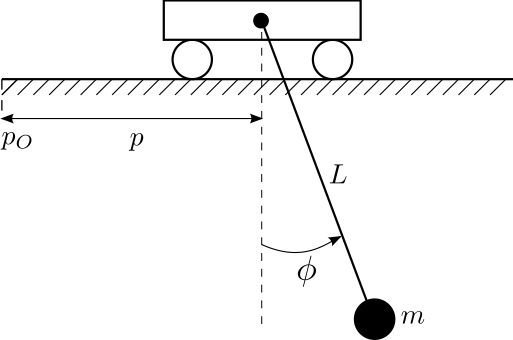
We consider the following tutorial example: a crane with mass 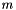$ m $ , line length 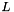$ L $ , excitation angle 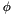$\phi$ , and horizontal trolley position 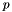$p$ . Our control input is the acceleration 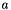$ a $ of the trolley. With 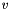$ v $ being the trolley velocity and 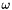$\omega$ being the angular velocity of the mass point, the system can be described by a simple but non-linear differential equation system:

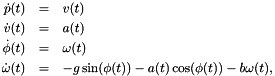
$\begin{eqnarray*} \dot p(t) &=& v(t)\\ \dot v(t) &=& a(t)\\ \dot \phi(t) &=& \omega(t)\\ \dot \omega(t) &=& -g \sin(\phi(t)) - a(t) \cos(\phi(t)) - b \omega(t), \end{eqnarray*}$

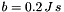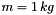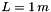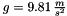where $b= 0.2 \, \text{J} \, \text{s}$ is a positive damping constant and we use the parameters $m = 1 \, \text{kg}$ , $L = 1 \, \text{m}$ , and $g = 9.81 \, \frac{\text{m}}{\text{s}^2}$ .

Our aim is to repeatedly solve the following Optimal Control Problem (OCP):

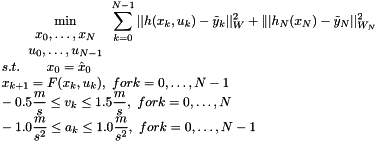
$\begin{align*} \displaystyle \min_{ \begin{array}{c} x_0, \ldots, x_{N} \\ u_0, \ldots, u_{N-1} \end{array}} & \displaystyle\sum_{k=0}^{N-1} ||h(x_k,u_k) - \tilde{y}_k ||^2_{W} +\||h_{N}(x_N) - \tilde{y}_N||^2_{W_{N}} \\ \text{s.t.} \quad\quad & x_0 = \hat x_0 \\ & x_{k+1} = F(x_k, u_k),\ \text{for } k = 0, \ldots, N-1 \\ & -0.5 \frac{\text{m}}{\text{s}} \leq v_k \leq 1.5 \frac{\text{m}}{\text{s}},\ \text{for } k = 0, \ldots, N \\ & -1.0 \frac{\text{m}}{\text{s}^2} \leq a_k \leq 1.0 \frac{\text{m}}{\text{s}^2},\ \text{for } k = 0, \ldots, N-1 \end{align*}$

where 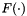$F(\cdot)$ describes the discretized system dynamics, previously described. For simplicity, we will define reference functions as follows:

$\begin{align*} h &= [p\ v\ \phi\ \omega\ a]^T,\\ h_N &= [p\ v\ \phi\ \omega]^T, \end{align*}$

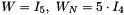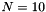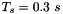together with the weighting matrices $W = I_5, \ W_N = 5\cdot I_4$ . For this example, we chose to use $ N = 10 $ control (prediction) intervals, and sampling time of $T_s = 0.3\ \text{s}$ .

Generating Code

Outline

In order to generate optimized code for this tutorial example using the CGT, the following steps are required:

Setup a source file describing your nonlinear MPC problem in ACADO syntax, defining desired options and specifying a target directory for the exported code. Compile this source file.

Run your compiled source file to export your code (i.e. the complete nonlinear MPC algorithm) into the target directory.

In case you are using the qpOASES QP solver, you will need to copy the solver source code files in the export folder, more precisely in the sub-folder qpoases.

We will now describe these steps in detail.

Formulating Your Nonlinear MPC Problem

We will now discuss step-by-step a possible nonlinear MPC formulation of the tutorial example. The full source code can also be found at examples/code_generation/getting_started.cpp. Please consult the ACADO User's Manual for more details on the ACADO syntax.

First of all, we need to formulate the ODE describing the crane in ACADO syntax. Together with the required header and namespace specification, this can read as follows:

 {.cpp}
#include <acado_toolkit.hpp>

int main( )
{
        USING_NAMESPACE_ACADO

        // Variables:
        DifferentialState   p    ;  // the trolley position
        DifferentialState   v    ;  // the trolley velocity 
        DifferentialState   phi  ;  // the excitation angle
        DifferentialState   omega;  // the angular velocity
        Control             a    ;  // the acc. of the trolley

        const double     g = 9.81;  // the gravitational constant 
        const double     b = 0.20;  // the friction coefficient

        // Model equations:
        DifferentialEquation f; 

        f << dot( p ) == v;
        f << dot( v ) == a;
        f << dot( phi ) == omega;
        f << dot( omega ) == -g * sin(phi) - a * cos(phi) - b * omega;

At the top four differential states and one control input are declared. Afterwards, an ODE comprising the four differential equations describing the crane dynamics are defined.

We use this ODE formulation to setup an optimal control problem (OCP) to be solved at each MPC sampling instant:

 {.cpp}
        // Reference functions and weighting matrices:
        Function h, hN;
        h << p << v << phi << omega << a;
        hN << p << v << phi << omega;

        Matrix W = eye( h.getDim() );
        Matrix WN = eye( hN.getDim() );
        WN *= 5;

        //
        // Optimal Control Problem
        //
        OCP ocp(0.0, 3.0, 10);

        ocp.subjectTo( f );

        ocp.minimizeLSQ(W, h);
        ocp.minimizeLSQEndTerm(WN, hN);

        ocp.subjectTo( -1.0 <= a <= 1.0 );
        ocp.subjectTo( -0.5 <= v <= 1.5 );

The above code snippet starts with defining the weighting matrices and reference function of the objective function. Afterwards, an OCP is defined over the time horizon $[0,3\,\text{s}]$ to be divided into 10 control intervals of equal length. Finally, the weighting matrices for the objective function are set (note that defining an end term is optional) and the OCP constraints are defined. Including the system dynamics into the constraints is mandatory, specifying limits on the control input or differential states is optional.

The OCP formulation is passed to the OCPexport class, several export options are set and code export to a given target directory is requested:

 {.cpp}
        // Export the code:
        OCPexport mpc( ocp );

        mpc.set( HESSIAN_APPROXIMATION,       GAUSS_NEWTON    );
        mpc.set( DISCRETIZATION_TYPE,         SINGLE_SHOOTING );
        mpc.set( INTEGRATOR_TYPE,             INT_RK4         );
        mpc.set( NUM_INTEGRATOR_STEPS,        30              );

        mpc.set( QP_SOLVER,                   QP_QPOASES      );
        mpc.set( GENERATE_TEST_FILE,          YES             );
        mpc.set( GENERATE_MAKE_FILE,          YES             );
        mpc.set( GENERATE_MATLAB_INTERFACE,   YES             );
        mpc.set( GENERATE_SIMULINK_INTERFACE, YES             );

        if (mpc.exportCode( "getting_started_export" ) != SUCCESSFUL_RETURN)
                exit( EXIT_FAILURE );

        mpc.printDimensionsQP( );

        return EXIT_SUCCESS;
}

All options and possible values are explained in detail in the ACADO User's Manual. We will shortly continue to prepare the specified target directory getting_started_export for the code export.

Finally, you need to compile this source file. You will need to rerun the make command in the main build folder. Please consult the toolkit web-page for further instruction on how to compile the code.

Preparing the Target Directory

The target directory has to be given relative to the location of the compiled source file that exports the code. Moreover, the CGT expects the target directory to contain the source code of a suitable QP solver. In case you are using the provided makefile to compile the generated code and wish to use Matlab MEX or Simulink interface, you will need to create a folder called qpoases in the main export folder. An embedded variant of this code comes along with your ACADO toolkit installation; you can find it at external_packages/qpoases. Do not rename it as the CGT expects the qpOASES code to be located within the sub-directory qpoases of your target directory.

Actually Exporting Your Nonlinear MPC Code

After compiling your nonlinear MPC problem formulation and preparing the desired target directory, you can actually export optimized C-code implementing a complete nonlinear MPC algorithm. For doing so, it is sufficient to simply run the compiled source file containing you problem formulation. Afterwards, you will find all necessary files within the target directory.

Running the Generated Code

Unless deactivated via the export options, the target directory also contains the generated file test.c with a main function template to run the generated nonlinear MPC algorithm. Let us browse through this file explaining the main steps:

Defining global constants, including headers and declare global variables:

 {.c}
#include "acado_common.h"
#include "acado_auxiliary_functions.h"

#include <stdio.h>
#include <string.h>

/* Some convenient definitions. */
#define NX          ACADO_NX  /* Number of differential state variables.  */
#define NXA         ACADO_NXA /* Number of algebraic variables. */
#define NU          ACADO_NU  /* Number of control inputs. */
#define NP          ACADO_NP  /* Number of parameters. */

#define NY          ACADO_NY  /* Number of measurements/references on nodes 0..N - 1. */
#define NYN         ACADO_NYN /* Number of measurements/references on node N. */

#define N           10        /* Number of intervals in the horizon. */

#define NUM_STEPS   5         /* Number of real-time iterations. */
#define VERBOSE     1         /* Show iterations: 1, silent: 0.  */

/* Global variables used by the solver. */
ACADOvariables acadoVariables;
ACADOworkspace acadoWorkspace;

At the beginning, the automatically generated header acado_common.h containing all forward declarations required to run the generated nonlinear MPC algorithm and the (optional) helper file acado_auxiliary_functions.h is included. A couple of global constants are defined in acado_common.h for convenience that contain the number of differential states, control inputs, control intervals, respectively. Please study this file. Moreover, global variables are declared: acadoVariables will be used later to call the algorithm, while acadoWorkspace is only used internally to store intermediate results.

Initializing the nonlinear MPC algorithm:

 {.c}
/* A template for testing of the solver. */
int main()
{
        /* Some temporary variables. */
        int    i, iter;
        timer t;
        
        /* Clear solver memory. */
        memset(&acadoWorkspace, 0, sizeof( acadoWorkspace ));
        memset(&acadoVariables, 0, sizeof( acadoVariables ));
        
        /* Initialize the solver. */
        initializeSolver();
        
        /* Initialize the states and controls. */
        for (i = 0; i < NX * (N + 1); ++i)  acadoVariables.x[ i ] = 0.0;
        for (i = 0; i < NU * N; ++i)  acadoVariables.u[ i ] = 0.0;
        
        /* Initialize the measurements/reference. */
        for (i = 0; i < NY * N; ++i)  acadoVariables.y[ i ] = 0.0;
        for (i = 0; i < NYN; ++i)  acadoVariables.yN[ i ] = 0.0;

        /* MPC: initialize the current state feedback. */
        for (i = 0; i < NX; ++i) acadoVariables.x0[ i ] = 0.1;
      
        if( VERBOSE ) printHeader();
        
        /* Prepare first step */
        preparationStep();

Before actually calling the nonlinear MPC algorithm, the struct acadoVariables needs to be initialised. acadoVariables.x and acadoVariables.u contain the initialisations of the differential states and control inputs at all interval points, respectively. acadoVariables.y and acadoVariables.yN contain the possibly time-varying reference values, respectively. Moreover, the array acadoVariables.x0 is initialised, whose dimension matches that of the differential states. At each call of the nonlinear MPC algorithm, it contains the current state measurement (or estimate), i.e. 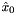$\hat{x}_0$ within the MPC formulation. Finally, the first step of the real-time iteration scheme is prepared.

Performing real-time iterations:

 {.c}
        /* Get the time before start of the loop. */
        tic( &t );

        /* The "real-time iterations" loop. */
        for(iter = 0; iter < NUM_STEPS; ++iter)
        {
        /* Perform the feedback step. */
                feedbackStep( );

                /* Apply the new control immediately to the process, first NU components. */
                
                if( VERBOSE ) printf("\tReal-Time Iteration %d:  KKT Tolerance = %.3e\n\n", iter, getKKT() );

                /* Optional: shift the initialization (look at acado_common.h). */
        shiftStates(2, 0, 0);
                shiftControls( 0 );

                /* Prepare for the next step. */
                preparationStep();
        }
        /* Read the elapsed time. */
        real_t te = toc( &t );

This code snippet illustrates how to call the real-time iteration algorithm. At each sampling instant, the user obtains the current state measurement. This measurement is then passed to the feedback step to obtain the optimized control inputs. Afterwards, initialization of control inputs and states might be shifted and the next iteration is prepared by calling preparationStep().

This sample main function illustrates the main steps to use the auto-generated nonlinear MPC algorithm. More algorithmic details can be found in the manual.

Unless deactivated via the export options, the target directory also contains a basic Makefile to facilitate compilation of the exported code and this sample main function. This Makefile can also create the library libacado_exported_rti.a which can be used for linking with external applications.

For more info, please go to the folder examples/code_generation/mpc_mhe and execute the example. Afterwards, in the export folder getting_started_export you will find Matlab MEX and Simulink demos which you can also execute and see performance of the exported code.