Public Member Functions | Private Types | Private Member Functions | Static Private Member Functions | Private Attributes
Eigen::MatrixPower< MatrixType > Class Template Reference

Class for computing matrix powers. More...

#include <MatrixPower.h>

List of all members.

Public Member Functions

Index cols () const
template<typename ResultType >
void compute (ResultType &res, RealScalar p)
 Compute the matrix power.
 MatrixPower (const MatrixType &A)
 Constructor.
const MatrixPowerRetval
< MatrixType > 		operator() (RealScalar p)
 Returns the matrix power.
Index rows () const

Private Types

enum  { RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef Matrix< ComplexScalar,
RowsAtCompileTime,
ColsAtCompileTime,
MatrixType::Options,
MaxRowsAtCompileTime,
MaxColsAtCompileTime > 		ComplexMatrix
typedef std::complex< RealScalar > ComplexScalar
typedef MatrixType::Index Index
typedef MatrixType::RealScalar RealScalar
typedef MatrixType::Scalar Scalar

Private Member Functions

template<typename ResultType >
void computeFracPower (ResultType &, RealScalar)
template<typename ResultType >
void computeIntPower (ResultType &, RealScalar)
RealScalar modfAndInit (RealScalar, RealScalar *)

Static Private Member Functions

template<int Rows, int Cols, int Options, int MaxRows, int MaxCols>
static void revertSchur (Matrix< ComplexScalar, Rows, Cols, Options, MaxRows, MaxCols > &res, const ComplexMatrix &T, const ComplexMatrix &U)
template<int Rows, int Cols, int Options, int MaxRows, int MaxCols>
static void revertSchur (Matrix< RealScalar, Rows, Cols, Options, MaxRows, MaxCols > &res, const ComplexMatrix &T, const ComplexMatrix &U)

Private Attributes

MatrixType::Nested m_A
RealScalar m_conditionNumber
ComplexMatrix m_fT
ComplexMatrix m_T
MatrixType m_tmp
ComplexMatrix m_U

Detailed Description

template<typename MatrixType>
class Eigen::MatrixPower< MatrixType >

Class for computing matrix powers.

Template Parameters:
MatrixTypetype of the base, expected to be an instantiation of the Matrix class template.

This class is capable of computing real/complex matrices raised to an arbitrary real power. Meanwhile, it saves the result of Schur decomposition if an non-integral power has even been calculated. Therefore, if you want to compute multiple (>= 2) matrix powers for the same matrix, using the class directly is more efficient than calling MatrixBase::pow().

Example: 

 Output: 


 

Definition at line 275 of file MatrixPower.h.


Member Typedef Documentation








template<typename MatrixType> 

      

        

          typedef Matrix<ComplexScalar, RowsAtCompileTime, ColsAtCompileTime, MatrixType::Options, MaxRowsAtCompileTime, MaxColsAtCompileTime> Eigen::MatrixPower< MatrixType >::ComplexMatrix [private]
        

      







Definition at line 326 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          typedef std::complex<RealScalar> Eigen::MatrixPower< MatrixType >::ComplexScalar [private]
        

      







Definition at line 324 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          typedef MatrixType::Index Eigen::MatrixPower< MatrixType >::Index [private]
        

      







Definition at line 286 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          typedef MatrixType::RealScalar Eigen::MatrixPower< MatrixType >::RealScalar [private]
        

      







Definition at line 285 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          typedef MatrixType::Scalar Eigen::MatrixPower< MatrixType >::Scalar [private]
        

      







Definition at line 284 of file MatrixPower.h.







Member Enumeration Documentation








template<typename MatrixType> 

      

        

          anonymous enum [private]
        

      






Enumerator: 


RowsAtCompileTime 



ColsAtCompileTime 



MaxRowsAtCompileTime 



MaxColsAtCompileTime 










Definition at line 278 of file MatrixPower.h.







Constructor & Destructor Documentation








template<typename MatrixType> 

      

        

          Eigen::MatrixPower< MatrixType >::MatrixPower 
          (
          const MatrixType & 
          A)
           [inline, explicit]
        

      







Constructor. 


Parameters:

  

    
[in]Athe base of the matrix power.

  

  




The class stores a reference to A, so it should not be changed (or destroyed) before evaluation. 



Definition at line 297 of file MatrixPower.h.







Member Function Documentation








template<typename MatrixType> 

      

        

          Index Eigen::MatrixPower< MatrixType >::cols 
          (
          void 
          )
           const [inline]
        

      







Definition at line 321 of file MatrixPower.h.













template<typename MatrixType > 



template<typename ResultType > 

      

        

          void Eigen::MatrixPower< MatrixType >::compute 
          (
          ResultType & 
          res, 
        

        

          
          
          RealScalar 
          p 
        

        

          
          )
          
        

      







Compute the matrix power. 


Parameters:

  

    
[in]pexponent, a real scalar. 

    
[out]res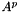$ A^p $ where A is specified in the constructor. 

  

  





Definition at line 356 of file MatrixPower.h.













template<typename MatrixType > 



template<typename ResultType > 

      

        

          void Eigen::MatrixPower< MatrixType >::computeFracPower 
          (
          ResultType & 
          res, 
        

        

          
          
          RealScalar 
          p 
        

        

          
          )
           [private]
        

      







Definition at line 416 of file MatrixPower.h.













template<typename MatrixType > 



template<typename ResultType > 

      

        

          void Eigen::MatrixPower< MatrixType >::computeIntPower 
          (
          ResultType & 
          res, 
        

        

          
          
          RealScalar 
          p 
        

        

          
          )
           [private]
        

      







Definition at line 398 of file MatrixPower.h.













template<typename MatrixType > 

      

        

          MatrixPower< MatrixType >::RealScalar Eigen::MatrixPower< MatrixType >::modfAndInit 
          (
          RealScalar 
          x, 
        

        

          
          
          RealScalar * 
          intpart 
        

        

          
          )
           [private]
        

      







Definition at line 373 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          const MatrixPowerRetval<MatrixType> Eigen::MatrixPower< MatrixType >::operator() 
          (
          RealScalar 
          p)
           [inline]
        

      







Returns the matrix power. 


Parameters:

  

    
[in]pexponent, a real scalar. 

  

  




Returns:
The expression 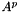$ A^p $, where A is specified in the constructor. 



Definition at line 307 of file MatrixPower.h.













template<typename MatrixType > 



template<int Rows, int Cols, int Options, int MaxRows, int MaxCols> 

      

        

          void Eigen::MatrixPower< MatrixType >::revertSchur 
          (
          Matrix< ComplexScalar, Rows, Cols, Options, MaxRows, MaxCols > & 
          res, 
        

        

          
          
          const ComplexMatrix & 
          T, 
        

        

          
          
          const ComplexMatrix & 
          U 
        

        

          
          )
           [inline, static, private]
        

      







Definition at line 428 of file MatrixPower.h.













template<typename MatrixType > 



template<int Rows, int Cols, int Options, int MaxRows, int MaxCols> 

      

        

          void Eigen::MatrixPower< MatrixType >::revertSchur 
          (
          Matrix< RealScalar, Rows, Cols, Options, MaxRows, MaxCols > & 
          res, 
        

        

          
          
          const ComplexMatrix & 
          T, 
        

        

          
          
          const ComplexMatrix & 
          U 
        

        

          
          )
           [inline, static, private]
        

      







Definition at line 436 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          Index Eigen::MatrixPower< MatrixType >::rows 
          (
          void 
          )
           const [inline]
        

      







Definition at line 320 of file MatrixPower.h.







Member Data Documentation








template<typename MatrixType> 

      

        

          MatrixType::Nested Eigen::MatrixPower< MatrixType >::m_A [private]
        

      







Definition at line 328 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          RealScalar Eigen::MatrixPower< MatrixType >::m_conditionNumber [private]
        

      







Definition at line 331 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          ComplexMatrix Eigen::MatrixPower< MatrixType >::m_fT [private]
        

      







Definition at line 330 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          ComplexMatrix Eigen::MatrixPower< MatrixType >::m_T [private]
        

      







Definition at line 330 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          MatrixType Eigen::MatrixPower< MatrixType >::m_tmp [private]
        

      







Definition at line 329 of file MatrixPower.h.













template<typename MatrixType> 

      

        

          ComplexMatrix Eigen::MatrixPower< MatrixType >::m_U [private]
        

      







Definition at line 330 of file MatrixPower.h.







The documentation for this class was generated from the following file:







acado

Author(s): Milan Vukov, Rien Quirynen

autogenerated on Sat Jun 8 2019 19:40:49