A bi conjugate gradient stabilized solver for sparse square problems. More...
#include <BiCGSTAB.h>
Public Types | |
| typedef MatrixType::Index | Index |
| typedef _MatrixType | MatrixType |
| typedef _Preconditioner | Preconditioner |
| typedef MatrixType::RealScalar | RealScalar |
| typedef MatrixType::Scalar | Scalar |
Public Member Functions | |
| template<typename Rhs , typename Dest > | |
| void | _solve (const Rhs &b, Dest &x) const |
| template<typename Rhs , typename Dest > | |
| void | _solveWithGuess (const Rhs &b, Dest &x) const |
| BiCGSTAB () | |
| BiCGSTAB (const MatrixType &A) | |
| template<typename Rhs , typename Guess > | |
| const internal::solve_retval_with_guess < BiCGSTAB, Rhs, Guess > | solveWithGuess (const MatrixBase< Rhs > &b, const Guess &x0) const |
| ~BiCGSTAB () | |
Private Types | |
| typedef IterativeSolverBase < BiCGSTAB > | Base |
Detailed Description
template<typename _MatrixType, typename _Preconditioner>
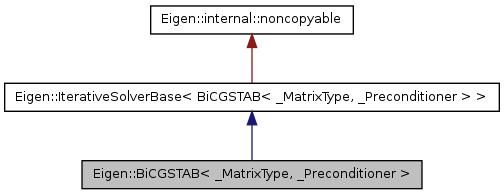
class Eigen::BiCGSTAB< _MatrixType, _Preconditioner >
A bi conjugate gradient stabilized solver for sparse square problems.
This class allows to solve for A.x = b sparse linear problems using a bi conjugate gradient stabilized algorithm. The vectors x and b can be either dense or sparse.
- Template Parameters:
-
_MatrixType the type of the sparse matrix A, can be a dense or a sparse matrix. _Preconditioner the type of the preconditioner. Default is DiagonalPreconditioner
The maximal number of iterations and tolerance value can be controlled via the setMaxIterations() and setTolerance() methods. The defaults are the size of the problem for the maximal number of iterations and NumTraits<Scalar>::epsilon() for the tolerance.
This class can be used as the direct solver classes. Here is a typical usage example:
int n = 10000; VectorXd x(n), b(n); SparseMatrix<double> A(n,n); // fill A and b BiCGSTAB<SparseMatrix<double> > solver; solver(A); x = solver.solve(b); std::cout << "#iterations: " << solver.iterations() << std::endl; std::cout << "estimated error: " << solver.error() << std::endl; // update b, and solve again x = solver.solve(b);
By default the iterations start with x=0 as an initial guess of the solution. One can control the start using the solveWithGuess() method. Here is a step by step execution example starting with a random guess and printing the evolution of the estimated error: *
x = VectorXd::Random(n); solver.setMaxIterations(1); int i = 0; do { x = solver.solveWithGuess(b,x); std::cout << i << " : " << solver.error() << std::endl; ++i; } while (solver.info()!=Success && i<100);
Note that such a step by step excution is slightly slower.
- See also:
- class SimplicialCholesky, DiagonalPreconditioner, IdentityPreconditioner
Definition at line 152 of file BiCGSTAB.h.
Member Typedef Documentation
typedef IterativeSolverBase<BiCGSTAB> Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::Base [private] |
Definition at line 154 of file BiCGSTAB.h.
| typedef MatrixType::Index Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::Index |
Reimplemented from Eigen::IterativeSolverBase< BiCGSTAB< _MatrixType, _Preconditioner > >.
Definition at line 163 of file BiCGSTAB.h.
| typedef _MatrixType Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::MatrixType |
Reimplemented from Eigen::IterativeSolverBase< BiCGSTAB< _MatrixType, _Preconditioner > >.
Definition at line 161 of file BiCGSTAB.h.
| typedef _Preconditioner Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::Preconditioner |
Reimplemented from Eigen::IterativeSolverBase< BiCGSTAB< _MatrixType, _Preconditioner > >.
Definition at line 165 of file BiCGSTAB.h.
| typedef MatrixType::RealScalar Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::RealScalar |
Reimplemented from Eigen::IterativeSolverBase< BiCGSTAB< _MatrixType, _Preconditioner > >.
Definition at line 164 of file BiCGSTAB.h.
| typedef MatrixType::Scalar Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::Scalar |
Reimplemented from Eigen::IterativeSolverBase< BiCGSTAB< _MatrixType, _Preconditioner > >.
Definition at line 162 of file BiCGSTAB.h.
Constructor & Destructor Documentation
| Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::BiCGSTAB | ( | ) | [inline] |
Default constructor.
Definition at line 170 of file BiCGSTAB.h.
| Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::BiCGSTAB | ( | const MatrixType & | A | ) | [inline] |
Initialize the solver with matrix A for further Ax=b solving.
This constructor is a shortcut for the default constructor followed by a call to compute().
- Warning:
- this class stores a reference to the matrix A as well as some precomputed values that depend on it. Therefore, if A is changed this class becomes invalid. Call compute() to update it with the new matrix A, or modify a copy of A.
Definition at line 182 of file BiCGSTAB.h.
| Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::~BiCGSTAB | ( | ) | [inline] |
Definition at line 184 of file BiCGSTAB.h.
Member Function Documentation
| void Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::_solve | ( | const Rhs & | b, |
| Dest & | x | ||
| ) | const [inline] |
Definition at line 224 of file BiCGSTAB.h.
| void Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::_solveWithGuess | ( | const Rhs & | b, |
| Dest & | x | ||
| ) | const [inline] |
Definition at line 204 of file BiCGSTAB.h.
| const internal::solve_retval_with_guess<BiCGSTAB, Rhs, Guess> Eigen::BiCGSTAB< _MatrixType, _Preconditioner >::solveWithGuess | ( | const MatrixBase< Rhs > & | b, |
| const Guess & | x0 | ||
| ) | const [inline] |
- Returns:
- the solution x of
 using the current decomposition of A x0 as an initial solution.
using the current decomposition of A x0 as an initial solution.
- See also:
- compute()
Definition at line 193 of file BiCGSTAB.h.
The documentation for this class was generated from the following file: