ecl_manipulators
Deploys various manipulation algorithms, currently just feedforward filters (interpolations).
- Homepage: http://wiki.ros.org/ecl_manipulators
Embedded Control Library
This group includes various structures and tools for generating
manipulator trajectories (interpolating methods etc).
Compiling & Linking
Since the manipulator classes are templatised headers, there is no need to directly link (however, it's dependencies will need linking).
Usage
Trajectory generation is usually done either in the joint angle space or in the cartesian space. All the classes in this library are configured appropriately via the Angle Type enumeration (Cartesian or JointAngle) type used as a template argument.
WayPoints
These are often also called via points or nodes depending on the context. They are used here as a means of representing the state of a manipulator at a particular point. A rough sequence of these can be then utilised to generate an interpolation with a much finer granularity.
Joint Angle Trajectories
WayPoints
Joint angle waypoints require alot of configuration, so the waypoint class provides methods for the programmer to manually do so:
The current interpolations are designed to relieve alot of the detail involved in configuring waypoints and generating trajectories. Depending on the interpolation, they will often use a heuristic or apply constraints to best solve the following waypoint properties:
- timestamp - interpolations will often stretch out the sequence to satisfy acceleration bounds.
- velocities - the nominal rates given above are typically used as a 'hint', but are reduced to satisfy constraints.
- accelerations - provided they stay within bounds, accelerations are usually automatically generated, usually with a continuity guarantee.
Practically, the interpolations use the nominalRates to initialise a guess for the waypoint timestamps. These are amended later to satisfy other interpolation constraints (such as maximum acceleration). If you set the nominalRate to 0.0, most interpolations will then look to the duration to set an initial guess for the waypoint timestamps.
Trajectories
All trajectory generating techniques work on the waypoint classfication given above. As noted above, one goal towards this is to try and make trajectory generation as smart as possible. I'd rather have it intelligently automate the generation of the data set on a little information as possible. Too often, trajectory generation requires alot of fiddling of the underlying data set, or guessing of parameters such as rates, accelerations and time values. Usually this guessing has no optimisation involved or intelligent heuristic applied.
The joint angle trajectory class applies this. It fulfills several features:
- Serves as a waypoint storage container.
- Saves various trajectory-wide parameters (such as joint motor accelerations).
- Allows generation of the trajectory spline functions using one of a various of interpolation techniques.
- Provides accessors to extract the value of the interpolated trajectories at any point.
The following code illustrates a sample trajectory generation flow:
Interpolations
Commonly either a linear interpolation with blends or a variant of a cubic spline is used. On a cheap robot arm though, these have a few problems since the motors suffer greatly from backlash and inaccuracies.
- Linear blends define a bang-bang acceleration to generate the trajectory (rough on the motors).
- Cubic splines do not have enough coefficients to ensure y' = y'' = 0 at the trajectory beginning and ending.
- Cubic splines do not ensure maximum acceleration bound constraints.
To get around this, we utilise a few different ideas to ensure the following problems dont exist.
- Stretch the interpolations to satisfy maximum acceleration bounds.
- Use a quintic on the first and last segments to ensure resting rates and accelerations.
- Alternatively, apply a pre/post pseudo waypoint and attach very small quintics to the front and back.
- Use C2 continuous splines to avoid bang-bang problems.
Quintic-Cubic-Quintic Interpolating Trajectories
For this, we attach a fully quintic polynomial at the front and back ends (first and last waypoints) and use a natural cubic spline in the middle. The natural cubic spline ensures C2 continuity and provides the connections to automatically ensure the quintics provide the zero'd boundary conditions.
Lastly, the interpolation algorithm firstly uses the waypoint nominal rate suggestions to define a rough time sequence and then uses an iterative technique to stretch the trajectory until the acceleration bounds are met.
Note, to configure everything for this interpolation algorithm, you will need:
- Waypoint angles (y's)
- Waypoint nominal rates or durations.
- Trajectory maximum acceleration bound.
Unfortunately, one problem with this is the quintic will often head in the wrong direction at the start of the motion so that it can meet whatever velocity and acceleration constraints are set up by the interior cubic spline at the second waypoint. To make sure this doesn't happen, you need to tune your waypoints carefully.

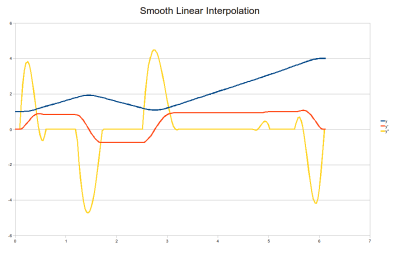
Smoothed Linear Interpolating Trajectories
This interpolation is like the tension spline at very high tension. It uses linear segments and quintic corners, as well as applying the same pre-post pseudo waypoint trick to guarantee resting constraints at the boundaries. It's a good alternative to the tension spline when you want almost exactly predictable motions rather than natural human like curves.
To configure everything, proceed as for the quintic-cubic-quintic.
Tension Interpolating Trajectories
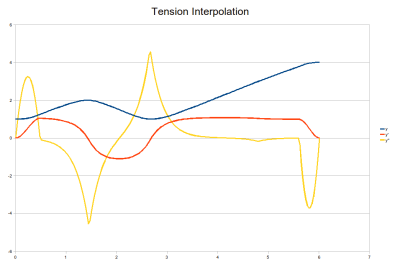
This interpolation is very similar to the quintic-cubic-quintic except that a tension spline is used in place of the natural spline and very small quintics are attached at the front and back via pseudo waypoints located very close to the actual starting and finishing waypoints.
A tension spline at low tension is just like the cubic (i.e. as tension -> 0.0, the spline becomes a cubic). By increasing the tension parameter to the interpolation algorithm, you can effectively tighten the polynomial until it starts looking more like the linear blend. This tends to provide more predictable motions and the acceleration is more tightly bound to zero most of the time (cubic spline accelerations will swing around fairly wildly).
To configure everything, proceed as for the quintic-cubic-quintic. The only addition is to supply a tension parameter when calling the interpolation algorithm.
Unit Tests
- src/test/waypoints.cpp
- src/test/trajectories.cpp
ChangeLog
- <b>Jul 09</b> : ecl::Trajectory<N,JointAngles> has a smooth linear spline interpolator.
- <b>Jul 09</b> : ecl::Trajectory<N,JointAngles> has a tension spline interpolator.
- <b>May 09</b> : ecl::Trajectory<N,JointAngles> has a quintic-cubic-quintic spline interpolator.
- <b>May 09</b> : ecl::Trajectory<N,JointAngles> formulation with waypoints finalised.
- <b>May 09</b> : ecl::WayPoint structure finalised.