
|
Functions | |
| static int | inv2 (const double *a, double *b) |
| static int | inv3 (const double *a, double *b) |
| static int | inv4 (const double *a, double *b) |
| void | matrix_add_sc (u32 n, u32 m, const double *a, const double *b, double gamma, double *c) |
| int | matrix_ataati (u32 n, u32 m, const double *a, double *b) |
| int | matrix_ataiat (u32 n, u32 m, const double *a, double *b) |
| int | matrix_atawati (u32 n, u32 m, const double *a, const double *w, double *b) |
| int | matrix_atwaiat (u32 n, u32 m, const double *a, const double *w, double *b) |
| void | matrix_copy (u32 n, u32 m, const double *a, double *b) |
| void | matrix_eye (u32 n, double *M) |
| int | matrix_inverse (u32 n, const double *const a, double *b) |
| void | matrix_multiply (u32 n, u32 m, u32 p, const double *a, const double *b, double *c) |
| int | matrix_pseudoinverse (u32 n, u32 m, const double *a, double *b) |
| void | matrix_reconstruct_udu (u32 n, double *U, double *D, double *M) |
| void | matrix_transpose (u32 n, u32 m, const double *a, double *b) |
| void | matrix_triu (u32 n, double *M) |
| void | matrix_udu (u32 n, double *M, double *U, double *D) |
| s32 | qrdecomp (const double *a, u32 rows, u32 cols, double *qt, double *r) |
| s32 | qrdecomp_square (const double *a, u32 rows, double *qt, double *r) |
| s32 | qrsolve (const double *a, u32 rows, u32 cols, const double *b, double *x) |
| void | qtmult (const double *qt, u32 n, const double *b, double *x) |
| static void | row_swap (double *a, double *b, u32 size) |
| static int | rref (u32 order, u32 cols, double *m) |
| void | rsolve (const double *r, u32 rows, u32 cols, const double *b, double *x) |
Detailed Description
Routines for working with matrices.
Function Documentation
| static int inv2 | ( | const double * | a, |
| double * | b | ||
| ) | [inline, static] |
Invert a 2x2 matrix. Calculate the inverse of a 2x2 matrix: 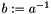
- Parameters:
-
a The matrix to invert (input) b Where to put the inverse (output)
- Returns:
- -1 if a is singular; 0 otherwise.
Definition at line 378 of file linear_algebra.c.
| static int inv3 | ( | const double * | a, |
| double * | b | ||
| ) | [inline, static] |
Invert a 3x3 matrix. Calculate the inverse of a 3x3 matrix: 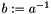
- Parameters:
-
a The matrix to invert (input) b Where to put the inverse (output)
- Returns:
- -1 if a is singular; 0 otherwise.
Definition at line 397 of file linear_algebra.c.
| static int inv4 | ( | const double * | a, |
| double * | b | ||
| ) | [inline, static] |
Invert a 4x4 matrix. Calculate the inverse of a 4x4 matrix: 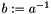
- Parameters:
-
a The matrix to invert (input) b Where to put the inverse (output)
- Returns:
- -1 if a is singular; 0 otherwise.
Definition at line 428 of file linear_algebra.c.
| void matrix_add_sc | ( | u32 | n, |
| u32 | m, | ||
| const double * | a, | ||
| const double * | b, | ||
| double | gamma, | ||
| double * | c | ||
| ) |
Add a matrix to a scaled matrix. Add two matrices: 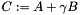 , where
, where 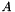 ,
, 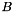 and
and 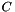 are matrices on
are matrices on 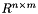 and
and 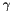 is a scalar coefficient.
is a scalar coefficient.
- Parameters:
-
n Number of rows in a, b and c m Number of columns in a, b and c a First matrix (unscaled) b Second matrix (will be scaled) gamma Coefficient for second matrix c Output (sum) matrix
Definition at line 920 of file linear_algebra.c.
| int matrix_ataati | ( | u32 | n, |
| u32 | m, | ||
| const double * | a, | ||
| double * | b | ||
| ) | [inline] |
Compute 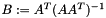 . Compute
. Compute 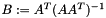 , where
, where 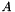 is a matrix on
is a matrix on 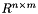 and
and 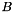 is (therefore) a matrix on
is (therefore) a matrix on 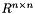 , for
, for 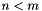 .
.
- Parameters:
-
n Number of rows in a and rows and columns in b m Number of columns in a a Input matrix b Output matrix
- Returns:
- -1 if n >= m or singular; 0 otherwise
Definition at line 756 of file linear_algebra.c.
| int matrix_ataiat | ( | u32 | n, |
| u32 | m, | ||
| const double * | a, | ||
| double * | b | ||
| ) | [inline] |
Compute 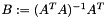 . Compute
. Compute 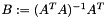 , where
, where 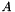 is a matrix on
is a matrix on 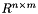 and
and 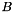 is (therefore) a matrix on
is (therefore) a matrix on 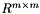 , for
, for  .
.
- Parameters:
-
n Number of rows in a m Number of columns in a and rows and columns in b a Input matrix b Output matrix
- Returns:
- -1 if n < m; 0 otherwise
Definition at line 737 of file linear_algebra.c.
| int matrix_atawati | ( | u32 | n, |
| u32 | m, | ||
| const double * | a, | ||
| const double * | w, | ||
| double * | b | ||
| ) | [inline] |
Compute 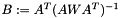 . Compute
. Compute 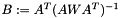 , where
, where 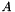 is a matrix on
is a matrix on 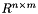 ,
, 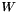 is a diagonal weighting matrix on
is a diagonal weighting matrix on 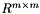 and
and 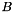 is (therefore) a matrix on
is (therefore) a matrix on 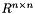 , for
, for 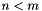 .
.
- Parameters:
-
n Number of rows in a and rows and columns in b m Number of columns in a a Input matrix w Diagonal vector of weighting matrix b Output matrix
- Returns:
- -1 if n <= m or singular; 0 otherwise
Definition at line 690 of file linear_algebra.c.
| int matrix_atwaiat | ( | u32 | n, |
| u32 | m, | ||
| const double * | a, | ||
| const double * | w, | ||
| double * | b | ||
| ) | [inline] |
Compute 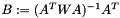 . Compute
. Compute 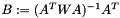 , where
, where 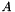 is a matrix on
is a matrix on 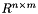 ,
, 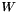 is a diagonal weighting matrix on
is a diagonal weighting matrix on 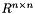 and
and 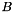 is (therefore) a matrix on
is (therefore) a matrix on 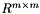 , for
, for  .
.
- Parameters:
-
n Number of rows in a m Number of columns in a and rows and columns in b a Input matrix w Diagonal vector of weighting matrix b Output matrix
- Returns:
- -1 if n <= m or singular; 0 otherwise
Definition at line 641 of file linear_algebra.c.
| void matrix_copy | ( | u32 | n, |
| u32 | m, | ||
| const double * | a, | ||
| double * | b | ||
| ) |
Copy a matrix. Copy a matrix: 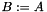 , where
, where 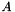 and
and 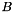 are matrices on
are matrices on 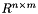 .
.
- Parameters:
-
n Number of rows in 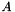 and
and 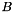
m Number of columns in 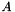 and
and 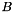
a Matrix to copy b Copied (output) matrix
Definition at line 955 of file linear_algebra.c.
| void matrix_eye | ( | u32 | n, |
| double * | M | ||
| ) |
Initialise an `n` x `n` identity matrix.
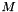 is a matrix on
is a matrix on 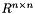
- Parameters:
-
n The size of the matrix. M Pointer to the matrix.
Definition at line 815 of file linear_algebra.c.
| int matrix_inverse | ( | u32 | n, |
| const double *const | a, | ||
| double * | b | ||
| ) | [inline] |
Invert a square matrix. Calculate the inverse of a square matrix: 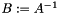 , where
, where 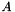 and
and 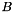 are matrices on
are matrices on 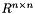 . For matrices size 4x4 and smaller, this is done by autogenerated hard-coded routines. For larger matrices, this is done by Gauss-Jordan elimination (which is
. For matrices size 4x4 and smaller, this is done by autogenerated hard-coded routines. For larger matrices, this is done by Gauss-Jordan elimination (which is 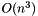 ).
).
- Parameters:
-
n The rank of a and b a The matrix to invert (input) b Where to put the inverse (output)
- Returns:
- -1 if a is singular; 0 otherwise.
Definition at line 528 of file linear_algebra.c.
| void matrix_multiply | ( | u32 | n, |
| u32 | m, | ||
| u32 | p, | ||
| const double * | a, | ||
| const double * | b, | ||
| double * | c | ||
| ) | [inline] |
Multiply two matrices. Multiply two matrices: 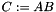 , where
, where 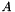 is a matrix on
is a matrix on 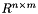 ,
, 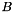 is a matrix on
is a matrix on 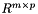 and
and 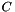 is (therefore) a matrix in
is (therefore) a matrix in 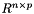 .
.
- Parameters:
-
n Number of rows in a and c m Number of columns in a and rows in b p Number of columns in b and c a First matrix to multiply b Second matrix to multiply c Output matrix
Definition at line 776 of file linear_algebra.c.
| int matrix_pseudoinverse | ( | u32 | n, |
| u32 | m, | ||
| const double * | a, | ||
| double * | b | ||
| ) |
Invert a non-square matrix (least-squares or least-norm solution). If 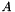 is of full rank, calculate the Moore-Penrose pseudoinverse
is of full rank, calculate the Moore-Penrose pseudoinverse 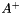 of a square matrix:
of a square matrix:
![\[ A \in \mathbb{R}^{n \times m} \]](form_46.png)
![\[ B := A^{+} = \begin{cases} (A^{T} A)^{-1} A^{T} & \text{if } n > m \\ A^{T} (A A^{T})^{-1} & \text{if } m > n \\ A^{-1} & \text{if } n = m \end{cases} \]](form_47.png)
If  , then
, then 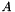 must be of full column rank, and
must be of full column rank, and 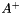 solves the linear least-squares (overconstrained) problem:
solves the linear least-squares (overconstrained) problem:
![\[ x' = A^{+} b = \underset{x}{min} \|Ax - b\|_{2} \]](form_49.png)
If 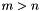 , then
, then 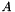 must be of full row rank, and
must be of full row rank, and 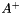 solves the linear least-norm (underconstrained) problem:
solves the linear least-norm (underconstrained) problem:
![\[ x' = A^{+} b = \underset{x}{min} \|x\|_{2} \text{s.t. } Ax = b \]](form_51.png)
If 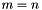 , then
, then 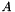 must be of full rank, and
must be of full rank, and 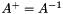 .
.
- Parameters:
-
n The number of rows in a m The number of columns in a a The matrix to invert (input) b Where to put the inverse (output)
- Returns:
- -1 if a is singular; 0 otherwise.
Definition at line 616 of file linear_algebra.c.
| void matrix_reconstruct_udu | ( | u32 | n, |
| double * | U, | ||
| double * | D, | ||
| double * | M | ||
| ) |
Reconstructs a matrix from its 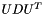 decomposition.
decomposition.
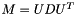 , where
, where 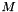 is a matrix on
is a matrix on 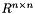 and
and 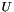 is a upper unit triangular matrix on
is a upper unit triangular matrix on 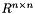 and
and 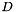 is a diagonal matrix expressed as a vector on
is a diagonal matrix expressed as a vector on  .
.
References:
- Gibbs, Bruce P. "Advanced Kalman Filtering, Least-Squares, and Modeling." John C. Wiley & Sons, Inc., 2011.
- Parameters:
-
n The size of the matrix. U Pointer to the upper unit triangular output matrix. D Pointer to the diagonal vector. M Pointer to the output matrix.
Definition at line 889 of file linear_algebra.c.
| void matrix_transpose | ( | u32 | n, |
| u32 | m, | ||
| const double * | a, | ||
| double * | b | ||
| ) |
Transpose a matrix. Transpose a matrix: 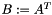 , where
, where 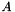 is a matrix on
is a matrix on 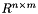 and
and 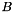 is (therefore) a matrix on
is (therefore) a matrix on 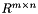 .
.
- Parameters:
-
n Number of rows in 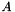 and columns in
and columns in 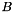
m Number of rows in 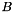 and columns in
and columns in 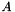
a Matrix to transpose b Transposed (output) matrix
Definition at line 938 of file linear_algebra.c.
| void matrix_triu | ( | u32 | n, |
| double * | M | ||
| ) |
Zero lower triangle of an `n` x `n` square matrix. Some routines designed to work on upper triangular matricies use the lower triangle as scratch space. This function zeros the lower triangle such that the matrix can be passed to a routine designed to act on a dense matrix.
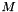 is a matrix on
is a matrix on 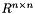
- Parameters:
-
n The size of the matrix. M Pointer to the matrix.
Definition at line 797 of file linear_algebra.c.
| void matrix_udu | ( | u32 | n, |
| double * | M, | ||
| double * | U, | ||
| double * | D | ||
| ) |
Performs the 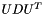 decomposition of a symmetric positive definite matrix. This is algorithm 10.2-2 of Gibbs [1].
decomposition of a symmetric positive definite matrix. This is algorithm 10.2-2 of Gibbs [1].
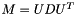 , where
, where 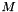 is a matrix on
is a matrix on 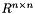 and
and 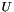 is (therefore) a upper unit triangular matrix on
is (therefore) a upper unit triangular matrix on 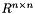 and
and 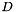 is a diagonal matrix expressed as a vector on
is a diagonal matrix expressed as a vector on 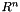 .
.
- Note:
- The M matrix is overwritten by this function.
References:
- Gibbs, Bruce P. "Advanced Kalman Filtering, Least-Squares, and Modeling." John C. Wiley & Sons, Inc., 2011.
- Parameters:
-
n The size of the matrix. M Pointer to the input matrix. U Pointer to the upper unit triangular output matrix. D Pointer to the diagonal vector.
Definition at line 845 of file linear_algebra.c.
QR decomposition of a matrix. Compute the QR decomposition of an arbitrary matrix 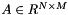 :
: 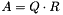 where
where 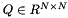 is an orthogonal matrix and
is an orthogonal matrix and 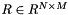 is an upper-triangular matrix.
is an upper-triangular matrix.
For an overdetermined (least-squares) problem, 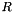 will be of the form
will be of the form
![\[ \begin{bmatrix} R' \\ 0 \end{bmatrix} \]](form_23.png)
where 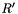 is an upper-triangular matrix on
is an upper-triangular matrix on 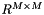 .
.
- Parameters:
-
A The matrix 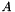 to decompose (input)
to decompose (input) rows How many rows in A cols How many columns in A qt 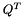 (output)
(output) r 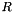 (output)
(output)
- Returns:
- -1 if A is singular; 0 otherwise;
Definition at line 97 of file linear_algebra.c.
| s32 qrdecomp_square | ( | const double * | a, |
| u32 | rows, | ||
| double * | qt, | ||
| double * | r | ||
| ) |
QR decomposition of a square matrix. Compute the QR decomposition of a square matrix 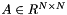 :
: 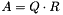 where
where 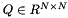 is an orthogonal matrix and
is an orthogonal matrix and 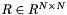 is an upper-triangular matrix.
is an upper-triangular matrix.
- Parameters:
-
A The matrix 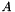 to decompose (input)
to decompose (input) rows How many rows in A qt 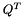 (output)
(output) r 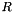 (output)
(output)
- Returns:
- -1 if A is singular; 0 otherwise;
Definition at line 251 of file linear_algebra.c.
Solve a linear system using the QR decomposition. Solve the linear system 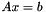 using the QR decomposition and backward substitution, where
using the QR decomposition and backward substitution, where 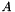 is a matrix on
is a matrix on 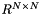 and
and 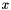 and
and 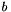 are vectors on
are vectors on 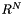 .
.
- Parameters:
-
a Matrix 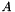 (input)
(input) rows Number of rows in a cols Number of columns in a b Vector 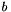 (input)
(input) x Vector 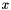 (output)
(output)
- Returns:
- -1 if a is singular; 0 otherwise.
Definition at line 359 of file linear_algebra.c.
Solve Qx = b for x. Since 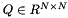 is an orthogonal matrix,
is an orthogonal matrix, 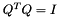 and therefore
and therefore 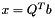 . This function computes
. This function computes 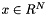 in this way.
in this way.
- Parameters:
-
qt 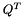 to be used to solve for x (input)
to be used to solve for x (input) n size of qt (it is square) b 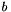 to be used to solve for x (input)
to be used to solve for x (input) x result of the linear solve (output)
Definition at line 311 of file linear_algebra.c.
Definition at line 462 of file linear_algebra.c.
Definition at line 473 of file linear_algebra.c.
Solve Rx = b for x. Solve 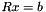 for
for 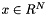 . Since
. Since 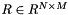 is upper-triangular, this can be done efficiently by back-substitution. This function has two important properties: it must never be called with an
is upper-triangular, this can be done efficiently by back-substitution. This function has two important properties: it must never be called with an 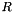 that results from the decomposition of a singular matrix, and it is safe to pass the same pointer for
that results from the decomposition of a singular matrix, and it is safe to pass the same pointer for 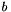 and
and 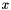 .
.
- Parameters:
-
r Upper-triangular 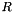 (input)
(input) rows Number of rows in r cols Number of columns in r b Vector 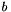 to solve against, from qtmult()
to solve against, from qtmult() x Solution vector 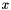 (output)
(output)
Definition at line 335 of file linear_algebra.c.