libvlfeat: Stochastic Dual Coordinate Ascent

Logistic

$(1 + e^{-y_i z})$

\[^*(u) = {cases} (1+u) (1+u) - u (-u), & -1 y_i u 0, \ +, & {otherwise} \ {cases}\]

Since each plane $- z - ^*_i(-) (z)$ bounds the loss from below, by substituting in $E()$ one can write a lower bound for the SVM objective \[ F(,) = {}{2} \|\|^2 - {1}{n}{i=1}^n (^ + ^*(-)) E(). \] for each setting of the *dual variables* $$. The dual objective function $D()$ is obtained by minimizing the lower bound $F(,)$ w.r.t. to $$: \[ D() = {} F(,) E(). \] The minimizer and the dual objective are now easy to find: \[ { () = {1}{ n} {i=1}^n = {1}{ n} X, D() = - {1}{2 n^2} ^ X^ X + {1}{n} {i=1}^n - ^*(-) } \] where $X = [, , ]$ is the data matrix. Since the dual is uniformly smaller than the primal, one has the *duality gap* bound: \[ D() P(^*) P(()) \] This bound can be used to evaluate how far off $()$ is from the primal minimizer $^*$. In fact, due to convexity, this bound can be shown to be zero when $^*$ is the dual maximizer (strong duality): \[ D(^*) = P(^*) = P((^*)), ^* = (^*). \]

Parametrization in C

Often a slightly different form of the SVM objective is considered, where a parameter $C$ is used to scale the loss instead of the regularizer:

\[ E_C() = {1}{2} \|\|^2 + C {i=1}^n ( , ) \]

This and the objective function $E()$ in $$ are equivalent (proportional) if

\[ = {1}{nC}, C = {1}{n}. \] up to an overall scaling factor to the problem.

This page describes the *Stochastic Dual Coordinate Ascent* (SDCA) linear SVM solver. Please see Support Vector Machines (SVM) for an overview of VLFeat SVM support.

SDCA maximizes the dual SVM objective (see svm-dual-problem for a derivation of this expression):

\[ D() = - {1}{2 n^2} ^ X^ X + {1}{n} {i=1}^n - ^*(-) \]

where $X$ is the data matrix. Recall that the primal parameter corresponding to a given setting of the dual variables is:

\[ () = {1}{ n} {i=1}^n = {1}{ n} X \]

In its most basic form, the *SDCA algorithm* can be summarized as follows:

Let $ = 0$.
Until the duality gap $P(()) - D() < $
- Pick a dual variable $q$ uniformly at random in $1, , n$.
- Maximize the dual with respect to this variable: $ = {} D( + )$
- Update ${t+1} = {t} + $.

In VLFeat, we partially use the nomenclature from [shwartz13a-dual]} and [hsieh08a-dual]}.

Dual coordinate maximization

The updated dual objective can be expanded as: \[ D( + ) = {const.}

{1}{2 n^2} ^ ()^2
{1}{n} ^ {X}{ n}
{1}{n} ^*_q(- - ) \] This can also be written as
$\begin{align*} D(\balpha_t + \be_q \Delta\alpha_q) &\propto - \frac{A}{2} (\Delta\alpha_q)^2 - B \Delta\alpha_q - \ell^*_q(- \alpha_q - \Delta\alpha_q), \\ A &= \frac{1}{\lambda n} \bx_q^\top \bx_q = \frac{1}{\lambda n} \| \bx_q \|^2, \\ B &= \bx_q^\top \frac{X\balpha_t}{\lambda n} = \bx_q^\top \bw_t. \end{align*}$
Maximizing this quantity in the scalar variable $$ is usually not difficult. It is convenient to store and incrementally update the model $$ after the optimal step $$ has been determined: \[ = {X }{ n}, {t+1} = + {1}{ n } . \]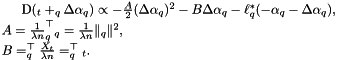

For example, consider the hinge loss as given in Advanced SVM topics : \[ ^*(u) = {cases} y_q u, & -1 y_q u 0, \ +, & {otherwise}. {cases} \] The maximizer $$ of the update objective must be in the range where the conjugate loss is not infinite. Ignoring such bounds, the update can be obtained by setting the derivative of the objective to zero, obtaining \[ { }= {y_q - B}{A}. \] Note that $B$ is simply current score associated by the SVM to the sample $$. Incorporating the constraint $-1 - y_q ( + ) 0$, i.e. $0 y_q ( + ) 1$, one obtains the update \[ = y_q , , y_q ( { } + )