libvlfeat: Simple Linear Iterative Clustering (SLIC)

Author:: Andrea Vedaldi

slic.h implements the *Simple Linear Iterative Clustering* (SLIC) algorithm, an image segmentation method described in [achanta10slic]}.

Overview

SLIC [achanta10slic]} is a simple and efficient method to decompose an image in visually homogeneous regions. It is based on a spatially localized version of k-means clustering. Similar to mean shift or quick shift (quickshift.h), each pixel is associated to a feature vector

$\Psi(x,y) = \left[ \begin{array}{c} \lambda x \\ \lambda y \\ I(x,y) \end{array} \right]$

and then k-means clustering is run on those. As discussed below, the coefficient $\lambda$ balances the spatial and appearance components of the feature vectors, imposing a degree of spatial regularization to the extracted regions.

SLIC takes two parameters: the nominal size of the regions (superpixels) regionSize and the strength of the spatial regularization regularizer. The image is first divided into a grid with step regionSize. The center of each grid tile is then used to initialize a corresponding k-means (up to a small shift to avoid image edges). Finally, the k-means centers and clusters are refined by using the Lloyd algorithm, yielding segmenting the image. As a further restriction and simplification, during the k-means iterations each pixel can be assigned to only the 2 x 2 centers corresponding to grid tiles adjacent to the pixel.

The parameter regularizer sets the trade-off between clustering appearance and spatial regularization. This is obtained by setting

$\lambda = \frac{\mathtt{regularizer}}{\mathtt{regionSize}}$

in the definition of the feature $\psi(x,y)$ .

After the k-means step, SLIC optionally removes any segment whose area is smaller than a threshld minRegionSize by merging them into larger ones.

Usage from the C library

To compute the SLIC superpixels of an image use the function vl_slic_segment.

Technical details

SLIC starts by dividing the image domain into a regular grid with $M \times N$ tiles, where

$M = \lceil \frac{\mathtt{imageWidth}}{\mathtt{regionSize}} \rceil, \quad N = \lceil \frac{\mathtt{imageHeight}}{\mathtt{regionSize}} \rceil.$

A region (superpixel or k-means cluster) is initialized from each grid center

$x_i = \operatorname{round} i \frac{\mathtt{imageWidth}}{\mathtt{regionSize}} \quad y_j = \operatorname{round} j \frac{\mathtt{imageWidth}}{\mathtt{regionSize}}.$

In order to avoid placing these centers on top of image discontinuities, the centers are then moved in a 3 x 3 neighbourohood to minimize the edge strength

$\operatorname{edge}(x,y) = \| I(x+1,y) - I(x-1,y) \|_2^2 + \| I(x,y+1) - I(x,y-1) \|_2^2.$

Then the regions are obtained by running k-means clustering, started from the centers

$C = \{ \Psi(x_i,y_j), i=0,1,\dots,M-1\ j=0,1,\dots,N-1 \}$

thus obtained. K-means uses the standard LLoyd algorithm alternating assigning pixels to the clostest centers a re-estiamting the centers as the average of the corresponding feature vectors of the pixel assigned to them. The only difference compared to standard k-means is that each pixel can be assigned only to the center originated from the neighbour tiles. This guarantees that there are exactly four pixel-to-center comparisons at each round of minimization, which threfore cost 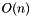$ O(n) $ , where $ n $ is the number of superpixels.

After k-means has converged, SLIC eliminates any connected region whose area is less than minRegionSize pixels. This is done by greedily merging regions to neighbour ones: the pixels $ p $ are scanned in lexicographical order and the corresponding connected components are visited. If a region has already been visited, it is skipped; if not, its area is computed and if this is less than minRegionSize its label is changed to the one of a neighbour region at $ p $ that has already been vistied (there is always one except for the very first pixel).