HessenbergDecomposition< _MatrixType > Class Template Reference

Reduces a squared matrix to an Hessemberg form. More...

#include <HessenbergDecomposition.h>

List of all members.

Public Types
enum	{ Size = MatrixType::RowsAtCompileTime, SizeMinusOne }
typedef Matrix< Scalar, SizeMinusOne, 1 >	CoeffVectorType
typedef NestByValue < DiagonalCoeffs< MatrixType > >::RealReturnType	DiagonalReturnType
typedef Matrix< RealScalar, Size, 1 >	DiagonalType
typedef _MatrixType	MatrixType
typedef NumTraits< Scalar >::Real	RealScalar
typedef MatrixType::Scalar	Scalar
typedef NestByValue < DiagonalCoeffs< NestByValue < Block< MatrixType, SizeMinusOne, SizeMinusOne > > > >::RealReturnType	SubDiagonalReturnType
typedef Matrix< RealScalar, SizeMinusOne, 1 >	SubDiagonalType
Public Member Functions
void	compute (const MatrixType &matrix)
	HessenbergDecomposition (const MatrixType &matrix)
	HessenbergDecomposition (int size=Size==Dynamic?2:Size)
CoeffVectorType	householderCoefficients (void) const
MatrixType	matrixH (void) const
MatrixType	matrixQ (void) const
const MatrixType &	packedMatrix (void) const
Protected Attributes
CoeffVectorType	m_hCoeffs
MatrixType	m_matrix
Static Private Member Functions
static void	_compute (MatrixType &matA, CoeffVectorType &hCoeffs)

---

Detailed Description

template<typename _MatrixType>
class HessenbergDecomposition< _MatrixType >

Reduces a squared matrix to an Hessemberg form.

Parameters:

MatrixType

the type of the matrix of which we are computing the Hessenberg decomposition

This class performs an Hessenberg decomposition of a matrix 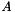such that: 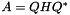where 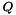is unitary and 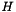a Hessenberg matrix.

See also:

class Tridiagonalization, class Qr

Definition at line 42 of file HessenbergDecomposition.h.

---

Member Typedef Documentation

template<typename _MatrixType >

typedef Matrix<Scalar, SizeMinusOne, 1> HessenbergDecomposition< _MatrixType >::CoeffVectorType

Definition at line 57 of file HessenbergDecomposition.h.

template<typename _MatrixType >

typedef NestByValue<DiagonalCoeffs<MatrixType> >::RealReturnType HessenbergDecomposition< _MatrixType >::DiagonalReturnType

Definition at line 61 of file HessenbergDecomposition.h.

template<typename _MatrixType >

typedef Matrix<RealScalar, Size, 1> HessenbergDecomposition< _MatrixType >::DiagonalType

Definition at line 58 of file HessenbergDecomposition.h.

template<typename _MatrixType >

typedef _MatrixType HessenbergDecomposition< _MatrixType >::MatrixType

Definition at line 46 of file HessenbergDecomposition.h.

template<typename _MatrixType >

typedef NumTraits<Scalar>::Real HessenbergDecomposition< _MatrixType >::RealScalar

Definition at line 48 of file HessenbergDecomposition.h.

template<typename _MatrixType >

typedef MatrixType::Scalar HessenbergDecomposition< _MatrixType >::Scalar

Definition at line 47 of file HessenbergDecomposition.h.

template<typename _MatrixType >

typedef NestByValue<DiagonalCoeffs< NestByValue<Block<MatrixType,SizeMinusOne,SizeMinusOne> > > >::RealReturnType HessenbergDecomposition< _MatrixType >::SubDiagonalReturnType

Definition at line 64 of file HessenbergDecomposition.h.

template<typename _MatrixType >

typedef Matrix<RealScalar, SizeMinusOne, 1> HessenbergDecomposition< _MatrixType >::SubDiagonalType

Definition at line 59 of file HessenbergDecomposition.h.

---

Member Enumeration Documentation

template<typename _MatrixType >

anonymous enum

Enumerator:

Size
SizeMinusOne

Definition at line 50 of file HessenbergDecomposition.h.

---

Constructor & Destructor Documentation

template<typename _MatrixType >

HessenbergDecomposition< _MatrixType >::HessenbergDecomposition

(

int

size = Size==Dynamic ? 2 : Size

)

[inline]

This constructor initializes a HessenbergDecomposition object for further use with HessenbergDecomposition::compute()

Definition at line 69 of file HessenbergDecomposition.h.

template<typename _MatrixType >

HessenbergDecomposition< _MatrixType >::HessenbergDecomposition

(

const MatrixType &

matrix

)

[inline]

Definition at line 73 of file HessenbergDecomposition.h.

---

Member Function Documentation

template<typename MatrixType >

void HessenbergDecomposition< MatrixType >::_compute	(	MatrixType &	matA,
		CoeffVectorType &	hCoeffs
	)			[inline, static, private]

Definition at line 142 of file HessenbergDecomposition.h.

template<typename _MatrixType >

void HessenbergDecomposition< _MatrixType >::compute

(

const MatrixType &

matrix

)

[inline]

Computes or re-compute the Hessenberg decomposition for the matrix matrix.

This method allows to re-use the allocated data.

Definition at line 84 of file HessenbergDecomposition.h.

template<typename _MatrixType >

CoeffVectorType HessenbergDecomposition< _MatrixType >::householderCoefficients

(

void

)

const [inline]

Returns:

the householder coefficients allowing to reconstruct the matrix Q from the packed data.

See also:

packedMatrix()

Definition at line 96 of file HessenbergDecomposition.h.

template<typename MatrixType >

HessenbergDecomposition< MatrixType >::MatrixType HessenbergDecomposition< MatrixType >::matrixH

(

void

)

const [inline]

constructs and returns the matrix H. Note that the matrix H is equivalent to the upper part of the packed matrix (including the lower sub-diagonal). Therefore, it might be often sufficient to directly use the packed matrix instead of creating a new one.

Definition at line 239 of file HessenbergDecomposition.h.

template<typename MatrixType >

HessenbergDecomposition< MatrixType >::MatrixType HessenbergDecomposition< MatrixType >::matrixQ

(

void

)

const [inline]

reconstructs and returns the matrix Q

Definition at line 212 of file HessenbergDecomposition.h.

template<typename _MatrixType >

const MatrixType& HessenbergDecomposition< _MatrixType >::packedMatrix

(

void

)

const [inline]

Returns:

the internal result of the decomposition.

The returned matrix contains the following information:

• the upper part and lower sub-diagonal represent the Hessenberg matrix H
• the rest of the lower part contains the Householder vectors that, combined with Householder coefficients returned by householderCoefficients(), allows to reconstruct the matrix Q as follow: Q = H_{N-1} ... H_1 H_0 where the matrices H are the Householder transformation: H_i = (I - h_i * v_i * v_i') where h_i == householderCoefficients()[i] and v_i is a Householder vector: v_i = [ 0, ..., 0, 1, M(i+2,i), ..., M(N-1,i) ]

See LAPACK for further details on this packed storage.

Definition at line 113 of file HessenbergDecomposition.h.

---

Member Data Documentation

template<typename _MatrixType >

CoeffVectorType HessenbergDecomposition< _MatrixType >::m_hCoeffs [protected]

Definition at line 124 of file HessenbergDecomposition.h.

template<typename _MatrixType >

MatrixType HessenbergDecomposition< _MatrixType >::m_matrix [protected]

Definition at line 123 of file HessenbergDecomposition.h.

---

The documentation for this class was generated from the following file:

• HessenbergDecomposition.h