TooN::SE2< Precision > Class Template Reference
[Transformation matrices]

#include <se2.h>

List of all members.

Public Member Functions

template<typename Accessor >
Matrix< 3, 3, Precision > adjoint (const Matrix< 3, 3, Precision, Accessor > &M) const
template<typename Accessor >
Vector< 3, Precision > adjoint (const Vector< 3, Precision, Accessor > &vect) const
template<int S, typename PV , typename Accessor >
SE2< Precision > exp (const Vector< S, PV, Accessor > &mu)
const SO2< Precision > & get_rotation () const
SO2< Precision > & get_rotation ()
 Returns the rotation part of the transformation as a SO2.
const Vector< 2, Precision > & get_translation () const
Vector< 2, Precision > & get_translation ()
 Returns the translation part of the transformation as a Vector.
SE2 inverse () const
 compute the inverse of the transformation
Vector< 3, Precision > ln () const
SE2 operator* (const SE2 &rhs) const
SE2 & operator*= (const SE2 &rhs)
template<int S, class P , class A >
 SE2 (const Vector< S, P, A > &v)
template<class A >
 SE2 (const SO2< Precision > &R, const Vector< 2, Precision, A > &T)
 SE2 ()
 Default constructor. Initialises the the rotation to zero (the identity) and the translation to zero.

Static Public Member Functions

template<int S, typename P , typename A >
static SE2 exp (const Vector< S, P, A > &vect)
static Matrix< 3, 3, Precision > generator (int i)
static Vector< 3, Precision > ln (const SE2 &se2)

Private Attributes

SO2< Precision > my_rotation
Vector< 2, Precision > my_translation

Related Functions

(Note that these are not member functions.)



template<int Rows, int C, typename PM , typename A , typename P >
Matrix< Rows, 3, typename
Internal::MultiplyType< PM, P >
::type > 		operator* (const Matrix< Rows, C, PM, A > &lhs, const SE2< P > &rhs)
template<int R, int Cols, typename PM , typename A , typename P >
Matrix< 3, Cols, typename
Internal::MultiplyType< P, PM >
::type > 		operator* (const SE2< P > &lhs, const Matrix< R, Cols, PM, A > &rhs)
template<int S, typename P , typename PV , typename A >
Vector< 3, typename
Internal::MultiplyType< PV, P >
::type > 		operator* (const Vector< S, PV, A > &lhs, const SE2< P > &rhs)
template<typename P , typename PV , typename A >
Vector< 2, typename
Internal::MultiplyType< P, PV >
::type > 		operator* (const SE2< P > &lhs, const Vector< 2, PV, A > &rhs)
template<int S, typename P , typename PV , typename A >
Vector< 3, typename
Internal::MultiplyType< P, PV >
::type > 		operator* (const SE2< P > &lhs, const Vector< S, PV, A > &rhs)
template<class Precision >
std::ostream & operator<< (std::ostream &os, const SE2< Precision > &rhs)

Detailed Description

template<typename Precision = double>
class TooN::SE2< Precision >

Represent a two-dimensional Euclidean transformation (a rotation and a translation). This can be represented by a 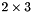$2\times 3$ matrix operating on a homogeneous co-ordinate, so that a vector 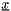$\underline{x}$ is transformed to a new location 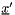$\underline{x}'$ by

\[\begin{aligned}\underline{x}' &= E\times\underline{x}\\ \begin{bmatrix}x'\\y'\end{bmatrix} &= \begin{pmatrix}r_{11} & r_{12} & t_1\\r_{21} & r_{22} & t_2\end{pmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}\end{aligned}\]

This transformation is a member of the Special Euclidean Lie group SE2. These can be parameterised with three numbers (in the space of the Lie Algebra). In this class, the first two parameters are a translation vector while the third is the amount of rotation in the plane as for SO2.

Definition at line 50 of file se2.h.

Constructor & Destructor Documentation

template<typename Precision = double>
TooN::SE2< Precision >::SE2 (  )  [inline]

Default constructor. Initialises the the rotation to zero (the identity) and the translation to zero.

Definition at line 40 of file se2.h.

template<typename Precision = double>
template<class A >
TooN::SE2< Precision >::SE2 ( const SO2< Precision > &  R,
const Vector< 2, Precision, A > &  T 
) [inline]

Definition at line 41 of file se2.h.

template<typename Precision = double>
template<int S, class P , class A >
TooN::SE2< Precision >::SE2 ( const Vector< S, P, A > &  v  )  [inline]

Definition at line 42 of file se2.h.

Member Function Documentation

template<typename Precision = double>
template<typename Accessor >
Matrix<3,3,Precision> TooN::SE2< Precision >::adjoint ( const Matrix< 3, 3, Precision, Accessor > &  M  )  const [inline]

Definition at line 111 of file se2.h.

template<typename Precision = double>
template<typename Accessor >
Vector<3, Precision> TooN::SE2< Precision >::adjoint ( const Vector< 3, Precision, Accessor > &  vect  )  const [inline]

transfers a vector in the Lie algebra, from one coord frame to another so that exp(adjoint(vect)) = (*this) * exp(vect) * (this->inverse())

Definition at line 101 of file se2.h.

template<typename Precision = double>
template<int S, typename PV , typename Accessor >
SE2<Precision> TooN::SE2< Precision >::exp ( const Vector< S, PV, Accessor > &  mu  )  [inline]

Definition at line 318 of file se2.h.

template<typename Precision = double>
template<int S, typename P , typename A >
static SE2 TooN::SE2< Precision >::exp ( const Vector< S, P, A > &  vect  )  [inline, static]

Exponentiate a Vector in the Lie Algebra to generate a new SE2. See the Detailed Description for details of this vector.

Parameters:
vect The Vector to exponentiate
template<typename Precision = double>
static Matrix<3,3, Precision> TooN::SE2< Precision >::generator ( int  i  )  [inline, static]

returns the generators for the Lie group. These are a set of matrices that form a basis for the vector space of the Lie algebra.

  • 0 is translation in x
  • 1 is translation in y
  • 2 is rotation in the plane

Definition at line 87 of file se2.h.

template<typename Precision = double>
const SO2<Precision>& TooN::SE2< Precision >::get_rotation (  )  const [inline]

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

Definition at line 47 of file se2.h.

template<typename Precision = double>
SO2<Precision>& TooN::SE2< Precision >::get_rotation (  )  [inline]

Returns the rotation part of the transformation as a SO2.

Definition at line 45 of file se2.h.

template<typename Precision = double>
const Vector<2, Precision>& TooN::SE2< Precision >::get_translation (  )  const [inline]

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

Definition at line 51 of file se2.h.

template<typename Precision = double>
Vector<2, Precision>& TooN::SE2< Precision >::get_translation (  )  [inline]

Returns the translation part of the transformation as a Vector.

Definition at line 49 of file se2.h.

template<typename Precision = double>
SE2 TooN::SE2< Precision >::inverse (  )  const [inline]

compute the inverse of the transformation

Definition at line 66 of file se2.h.

template<typename Precision = double>
Vector<3, Precision> TooN::SE2< Precision >::ln (  )  const [inline]

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

Definition at line 63 of file se2.h.

template<typename Precision >
Vector< 3, Precision > TooN::SE2< Precision >::ln ( const SE2< Precision > &  se2  )  [inline, static]

Take the logarithm of the matrix, generating the corresponding vector in the Lie Algebra. See the Detailed Description for details of this vector.

Definition at line 353 of file se2.h.

template<typename Precision = double>
SE2 TooN::SE2< Precision >::operator* ( const SE2< Precision > &  rhs  )  const [inline]

Right-multiply by another SE2 (concatenate the two transformations)

Parameters:
rhs The multipier

Definition at line 73 of file se2.h.

template<typename Precision = double>
SE2& TooN::SE2< Precision >::operator*= ( const SE2< Precision > &  rhs  )  [inline]

Self right-multiply by another SE2 (concatenate the two transformations)

Parameters:
rhs The multipier

Definition at line 77 of file se2.h.

Friends And Related Function Documentation

template<int Rows, int C, typename PM , typename A , typename P >
Matrix< Rows, 3, typename Internal::MultiplyType< PM, P >::type > operator* ( const Matrix< Rows, C, PM, A > &  lhs,
const SE2< P > &  rhs 
) [related]

Left-multiply with a Matrix<3>

Definition at line 297 of file se2.h.

template<int R, int Cols, typename PM , typename A , typename P >
Matrix< 3, Cols, typename Internal::MultiplyType< P, PM >::type > operator* ( const SE2< P > &  lhs,
const Matrix< R, Cols, PM, A > &  rhs 
) [related]

Right-multiply with a Matrix<3>

Definition at line 263 of file se2.h.

template<int S, typename P , typename PV , typename A >
Vector< 3, typename Internal::MultiplyType< PV, P >::type > operator* ( const Vector< S, PV, A > &  lhs,
const SE2< P > &  rhs 
) [related]

Left-multiply with a Vector<3>

Definition at line 229 of file se2.h.

template<typename P , typename PV , typename A >
Vector< 2, typename Internal::MultiplyType< P, PV >::type > operator* ( const SE2< P > &  lhs,
const Vector< 2, PV, A > &  rhs 
) [related]

Right-multiply with a Vector<2> (special case, extended to be a homogeneous vector)

Definition at line 195 of file se2.h.

template<int S, typename P , typename PV , typename A >
Vector< 3, typename Internal::MultiplyType< P, PV >::type > operator* ( const SE2< P > &  lhs,
const Vector< S, PV, A > &  rhs 
) [related]

Right-multiply with a Vector<3>

Definition at line 188 of file se2.h.

template<class Precision >
std::ostream & operator<< ( std::ostream &  os,
const SE2< Precision > &  rhs 
) [related]

Write an SE2 to a stream

Definition at line 141 of file se2.h.

Member Data Documentation

template<typename Precision = double>
SO2<Precision> TooN::SE2< Precision >::my_rotation [private]

Definition at line 121 of file se2.h.

template<typename Precision = double>
Vector<2, Precision> TooN::SE2< Precision >::my_translation [private]

Definition at line 122 of file se2.h.

The documentation for this class was generated from the following file:
 All Classes Namespaces Files Functions Variables Typedefs Friends Defines

libtoon
Author(s): Florian Weisshardt
autogenerated on Fri Jan 11 10:09:50 2013