shape_reconstruction: random_generator.h File Reference

#include <vcg/math/base.h>

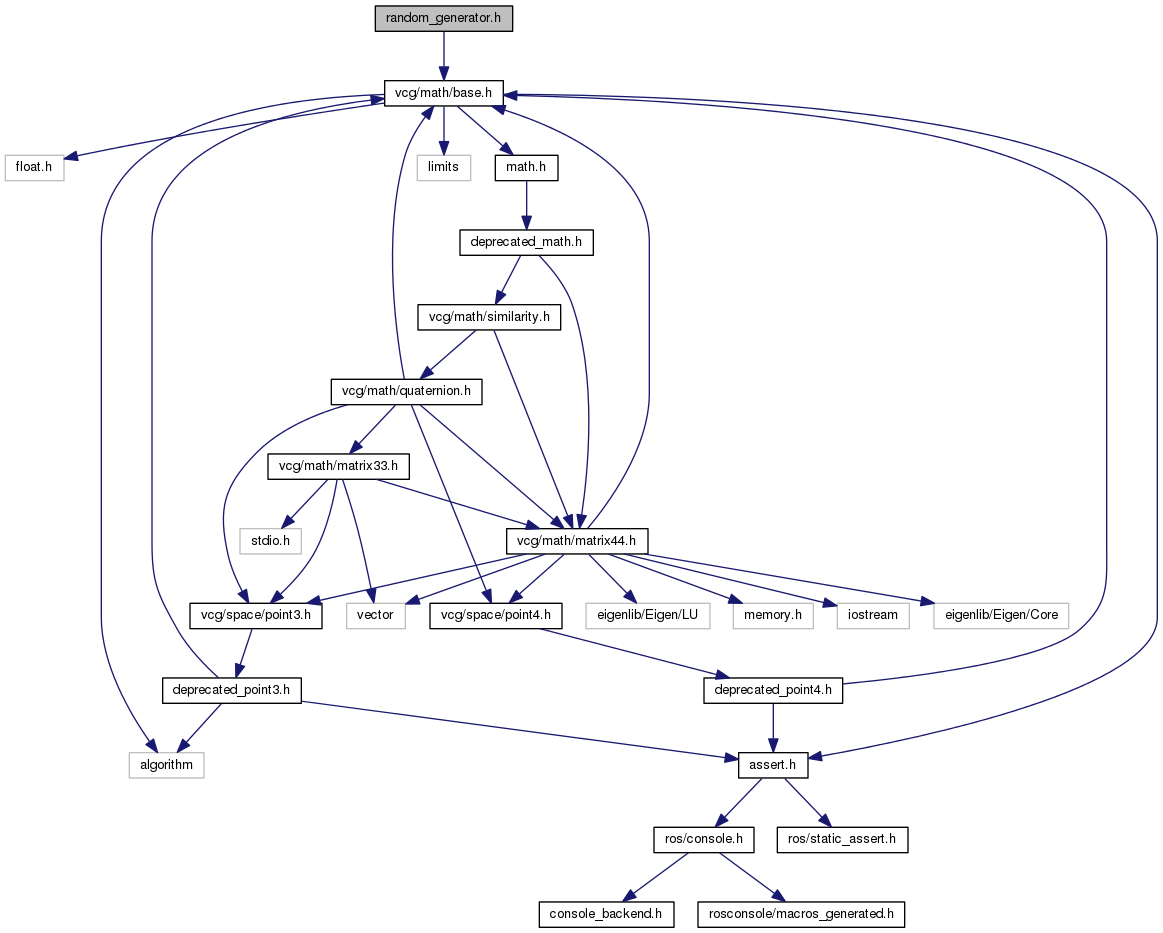
Include dependency graph for random_generator.h:

This graph shows which files directly or indirectly include this file:

Classes
class	vcg::math::MarsenneTwisterRNG
class	vcg::math::RandomGenerator
class	vcg::math::SubtractiveRingRNG
Namespaces
namespace	vcg
	*
namespace	vcg::math
Functions
double	vcg::math::box_muller (RandomGenerator &generator, double m, double s)
template<class ScalarType , class GeneratorType >
vcg::Point3< ScalarType >	vcg::math::GenerateBarycentricUniform (GeneratorType &rnd)
	Generate the barycentric coords of a random point over a single face, with a uniform distribution over the triangle. It uses the parallelogram folding trick.
template<class ScalarType , class GeneratorType >
vcg::Point3< ScalarType >	vcg::math::GeneratePointInBox3Uniform (GeneratorType &rnd, const Box3< ScalarType > &bb)
	Generate a random point insidie a box with uniform distribution.
template<class ScalarType , class GeneratorType >
vcg::Point3< ScalarType >	vcg::math::GeneratePointInUnitBallUniform (GeneratorType &rnd)
	generate a point inside a unit sphere with uniform distribution
template<class ScalarType , class GeneratorType >
vcg::Point3< ScalarType >	vcg::math::GeneratePointOnUnitSphereUniform (GeneratorType &rnd)
	Generate a point over the surface of a unit sphere with uniform distribution This is the algorithm proposed by George Marsaglia [1] to generate a point over a unit sphere Independently generate V1 and V2, taken from a uniform distribution on (-1,1) such that S=(V1^2+V2^2)<1.

Classes