Introduction
Classes representing continuously connected functions (splines) and some interpolation algorithms.
CompilingLinking
Include the following at the top of any translation unit that uses geometry functions or classes.
#include <ecl/geometry.hpp> // The classes using ecl::CubicSpline; using ecl::SmoothLinearSpline; using ecl::TensionSpline;
You will also need to link to -lecl_geometry.
Usage - CubicSpline
CubicSpline
The CubicSpline has a relatively simple c++ interface.
- Generation of splines via blueprint algorithms.
- Access for any x, the spline value, its derivative or its second derivative.
- A streamed (algebraic) representation.
BluePrints
The blueprints generate a cubic spline over a data set. Depending on the input constraints, the spline is generated rather differently. These can be accessed via static methods in the blueprint factory (ecl::BluePrintFactory< CubicSpline >) inherited by the CubicSpline class. For example:
CubicSpline cubic; cubic = CubicSpline::Natural(x_set, y_set); cubic = CubicSpline::ContinuousDerivatives(x_set, y_set, ydot_0, ydot_f); cubic = CubicSpline::DerivativeHeuristic(x_set, y_set, ydot_0, ydot_f);
Access
Access allows you to calculate the value of the spline at any point on its domain:
std::cout << "Value : " << cubic(3.2) << std::endl; std::cout << "1st Derivative: " << cubic.derivative(3.2) << std::endl; std::cout << "2nd Derivative: " << cubic.dderivative(3.2) << std::endl;
Algebraic
Streaming will provide an algebraic list of the cubic polynomials constituting the spline.
std::cout << cubic << std::endl; // Typical output // 1.00 + 2.31x + 3.00x^2 + 1.23x^3 // 0.00 + 1.42x + 5.20x^2 + 1.06x^3
Illustration
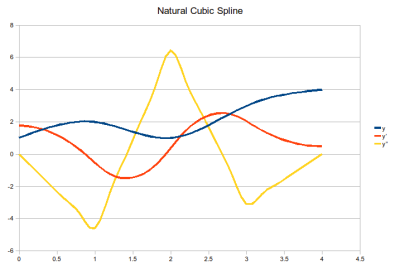
Usage - SmoothLinearSpline
SmoothLinearSpline
The SmoothLinearSpline simply linearly connects waypoints and adds a quintic polynomial curve to smooth the corners between each linear section. The shape of these corners is parameterised by a maximum curvature (acceleration) parameter.
Construction
Simply pass suitable x and y data sets along with a maximum curvature constraint parameter to the spline's constructor. Be sure to catch an exception if the construction should fail (this will occur if the maximum curvature constraint cannot be met).
double max_curvature = 5.0;
SmoothLinearSpline spline(x_set, y_set, max_curvature);
Access & Algebraic Forms
Access and streaming is similar to that for the cubic spline.
Illustration
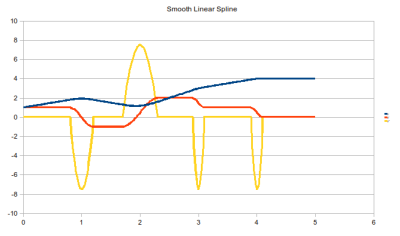
Usage - TensionSpline
TensionSpline
The TensionSpline represents a mathematically parameterised spline that portrays the whole family of splines from linearly connected segments through to cubic polynomials. To do this it uses the tension function. When connecting tension functions across a series of waypoints, the tension parameter provides this extra flexibility in controlling the shape of the spline.
- Low tension : it behaves exactly like the cubic spline.
- High tension : it behaves like a spline composed of linear segments.
Note that its primary advantages are that it is still C2 continuous and it is very easy to modify the resulting behaviour through tweaking of a single parameter.
BluePrints
There is currently only one blueprint (though variations are not difficult to create). It is very similar to the natural cubic spline (assumes zero boundary conditions for the second derivatives), the only difference being the addition of the tension parameter.
TensionSpline spline = TensionSpline::Natural(tension, x_set, y_set);
Access & Algebraic Forms
Access and streaming is similar to that for the cubic spline.
Illustration
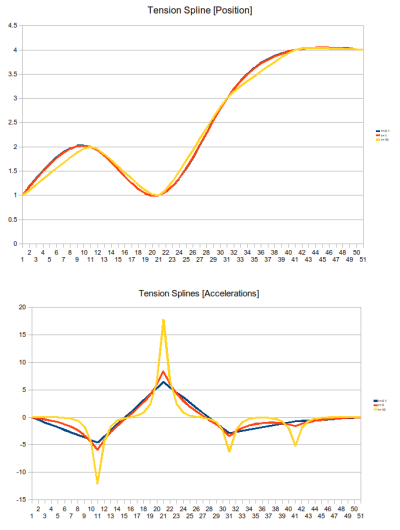
unitTests
- src/test/polynomials.cpp
- src/test/cubic_splines.cpp
- src/test/smooth_linear_splines.cpp
- src/test/tension_function.cpp
- src/test/tension_splines.cpp
ChangeLog
- Jul 09 : ecl::SmoothLinearSpline is a a smoothed, linearly blend spline (with quintics).
- May 09 : ecl::blueprints::C2TensionSpline is a c2 continuous tension spline interpolation.
- May 09 : ecl::TensionSpline is a representation for a tension spline.
- May 09 : ecl::TensionFunction is a representation for a tension function.
- May 09 : ecl::blueprints::C2CubicSpline is a special case of the C2CubicSpline, the natural cubic spline.
- May 09 : ecl::blueprints::C2CubicSpline is a blueprint for C2 continous splines over a set of data.
- May 09 : ecl::blueprints::DerivativeHeuristicCubicSpline uses an automated velocity based heuristic to generate a cubic spline on a data set.
- May 09 : ecl::BluePrintFactory<CubicSpline> is a blueprint factory for cubic splines.
- May 09 : ecl::CubicSpline is a typedef'd representation for a cubic spline.