libvlfeat: Agglomerative Information Bottleneck (AIB)

Author:: Brian Fulkerson; Andrea Vedaldi

aib.h implemens the Agglomerative Information Bottleneck (AIB) algorithm as first described in [slonim99agglomerative]}.

AIB takes a discrete valued feature 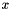$x$ and a label 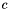$c$ and gradually compresses 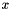$x$ by iteratively merging values which minimize the loss in mutual information $I(x,c)$ .

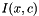While the algorithm is equivalent to the one described in [slonim99agglomerative]}, it has some speedups that enable handling much larger datasets. Let N be the number of feature values and C the number of labels. The algorithm of [slonim99agglomerative]} is 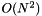$O(N^2)$ in space and 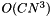$O(C N^3)$ in time. This algorithm is 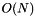$O(N)$ space and 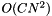$O(C N^2)$ time in common cases ( 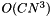in the worst case).

Overview

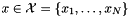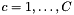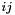Given a discrete feature $x \in \mathcal{X} = \{x_1,\dots,x_N\}$ and a category label $c = 1,\dots,C$ with joint probability $p(x,c)$ , AIB computes a compressed feature $[x]_{ij}$ by merging two values $x_i$ and $x_j$ . Among all the pairs $ij$ , AIB chooses the one that yields the smallest loss in the mutual information

$D_{ij} = I(x,c) - I([x]_{ij},c) = \sum_c p(x_i) \log \frac{p(x_i,c)}{p(x_i)p(c)} + \sum_c p(x_i) \log \frac{p(x_i,c)}{p(x_i)p(c)} - \sum_c (p(x_i)+p(x_j)) \log \frac {p(x_i,c)+p(x_i,c)}{(p(x_i)+p(x_j))p(c)}$

AIB iterates this procedure until the desired level of compression is achieved.

Algorithm details

Computing 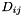$D_{ij}$ requires 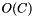$O(C)$ operations. For example, in standard AIB we need to calculate

Thus in a basic implementation of AIB, finding the optimal pair 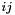$ij$ of feature values requires 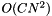$O(CN^2)$ operations in total. In order to join all the 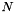$N$ values, we repeat this procedure 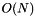$O(N)$ times, yielding $O(N^3 C)$ time and $O(1)$ space complexity (this does not account for the space need to store the input).

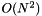The complexity can be improved by reusing computations. For instance, we can store the matrix $D = [ D_{ij} ]$ (which requires $O(N^2)$ space). Then, after joining 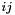$ij$ , all of the matrix D except the rows and columns (the matrix is symmetric) of indexes i and j is unchanged. These two rows and columns are deleted and a new row and column, whose computation requires $O(NC)$ operations, are added for the merged value $x_{ij}$ . 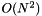Finding the minimal element of the matrix still requires $O(N^2)$ operations, so the complexity of this algorithm is $O(N^2C + N^3)$ time and 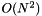space.

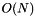We can obtain a much better expected complexity as follows. First, instead of storing the whole matrix D, we store the smallest element (index and value) of each row as $(q_i, D_i)$ (notice that this is also the best element of each column since D is symmetric). This requires $O(N)$ space and finding the minimal element of the matrix requires 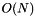$O(N)$ operations. After joining 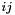$ij$ , we have to efficiently update this representation. This is done as follows:

The entries 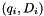and 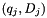are deleted.
A new entry 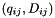$(q_{ij},D_{ij})$ for the joint value $x_{ij}$ is added. This requires 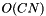operations.
We test which other entries 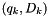need to be updated. Recall that 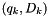means that, before the merge, the value closest to 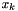was 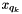at a distance 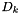. Then
- If 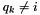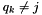$q_k \not = i$ , $q_k \not = j$ and $D_{k,ij} \geq D_k$ , then is still the closest element and we do not do anything.
- If 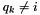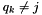$q_k \not = i$ , $q_k \not = j$ and $D_{k,ij} < D_k$ , then the closest element is 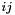and we update the entry in constant time.
- If 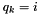or 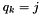, then we need to re-compute the closest element in 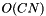operations.

This algorithm requires only 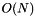$O(N)$ space and 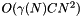$O(\gamma(N) C N^2)$ time, where 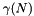$\gamma(N)$ is the expected number of times we fall in the last case. In common cases one has 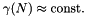$\gamma(N) \approx \mathrm{const.}$ , so the time saving is significant.