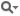00001 from Numeric import *
00002 from numpy import *
00003 from numpy.linalg import *
00004
00005 class Triangle:
00006 def __init__(self, verts):
00007
00008 A = array(verts[0])
00009 B = array(verts[1])
00010 C = array(verts[2])
00011 self.normal = cross(A-B, A-C)
00012 self.normal = self.normal / linalg.norm(self.normal)
00013 self.vertices = [A,B,C]
00014 self.childs = list()
00015 self.mappedNormals = list()
00016
00017 def getCenter(self):
00018 return (self.vertices[0]+self.vertices[1]+self.vertices[2])/3.
00019
00020 def reset(self):
00021 self.mappedNormals = list()
00022
00023 def normalize(self, vert):
00024
00025 r = vert;
00026 mag = vert[0] * vert[0] + vert[1] * vert[1] + vert[2] * vert[2];
00027 if (mag != 0.0):
00028 mag = 1.0 / sqrt(mag)
00029 r = r * mag
00030
00031 return r
00032
00033 def subdivide(self):
00034 a = self.normalize((self.vertices[0] + self.vertices[2]) / 2)
00035 b = self.normalize((self.vertices[0] + self.vertices[1]) / 2)
00036 c = self.normalize((self.vertices[1] + self.vertices[2]) / 2)
00037 self.childs.append(Triangle([self.vertices[0], b, a]))
00038 self.childs.append(Triangle([b, self.vertices[1], c]))
00039 self.childs.append(Triangle([a, b, c]))
00040 self.childs.append(Triangle([a, c, self.vertices[2]]))
00041 return self.childs
00042
00043 def dotProduct(self, n):
00044 return dot(self.normal,n)
00045
00046 def findCell(self, normal):
00047 if(len(self.childs) == 0):
00048 return self
00049
00050 maxDot = -1000
00051 cell = 0
00052
00053 for chi in self.childs:
00054 dotP = dot(normal,chi.normal)
00055 if dotP > maxDot:
00056 maxDot = dotP
00057 cell = chi
00058
00059 return cell.findCell(normal)
00060
00061 def addInfo(self, point, normal, interpolated, cellId):
00062 self.mappedNormals.append((point,normal, interpolated, cellId))