Speed, but not at the expense of accuracy.

TooN aims to be a fast library, and may choose between one of several algorithms depending on the size of the arguments. However TooN will never substitute a fast but numerically inferior algorithm. For example LU decomposition, Gaussian elimination and Gauss-Jordan reduction all have similar numerical properties for computing a matrix inverse. Direct inversino using Cramer's rule is significantly less stable, even for 3x3 matrices.

The following code computes a matrix inverse of the ill conditioned matrix:

using LU decomposition, Gauss-Jordan, pseudo-inverse with singular value decomposition and with Cramer's rule. The error is computed as:

The code is:

#include <TooN/TooN.h>
#include <TooN/helpers.h>
#include <TooN/LU.h>
#include <TooN/GR_SVD.h>
#include <TooN/gauss_jordan.h>
#include <TooN/gaussian_elimination.h>
#include <iomanip>
using namespace TooN;
using namespace std;
Matrix<3> invert_cramer(const Matrix<3>& A)
{
        Matrix<3> i;
        double t0 = A[0][0]*A[1][1]*A[2][2]-A[0][0]*A[1][2]*A[2][1]-A[1][0]*A[0][1]*A[2][2]+A[1][0]*A[0][2]*A[2][1]+A[2][0]*A[0][1]*A[1][2]-A[2][0]*A[0][2]*A[1][1];
        double idet = 1/t0;
        t0 = A[1][1]*A[2][2]-A[1][2]*A[2][1];
        i[0][0] = t0*idet;
        t0 = -A[0][1]*A[2][2]+A[0][2]*A[2][1];
        i[0][1] = t0*idet;
        t0 = A[0][1]*A[1][2]-A[0][2]*A[1][1];
        i[0][2] = t0*idet;
        t0 = -A[1][0]*A[2][2]+A[1][2]*A[2][0];
        i[1][0] = t0*idet;
        t0 = A[0][0]*A[2][2]-A[0][2]*A[2][0];
        i[1][1] = t0*idet;
        t0 = -A[0][0]*A[1][2]+A[0][2]*A[1][0];
        i[1][2] = t0*idet;
        t0 = A[1][0]*A[2][1]-A[1][1]*A[2][0];
        i[2][0] = t0*idet;
        t0 = -A[0][0]*A[2][1]+A[0][1]*A[2][0];
        i[2][1] = t0*idet;
        t0 = A[0][0]*A[1][1]-A[0][1]*A[1][0];
        i[2][2] = t0*idet;

        return i;
}


int main()
{
        Matrix<3> singular = Data(1, 2, 3,
                                                          1, 2, 3,
                                                          1, 2, 3);
        
        
        for(double i=0; i < 1000; i++)
        {
                double delta = pow(0.9, i);     
                
                //Make a poorly conditioned matrix
                Matrix<3> bad = singular;
                bad[2][2] += delta;
                bad[1][1] += delta;

                
                //Compute the inverse with LU decomposition
                Matrix<3> linv;
                LU<3> blu(bad);
                linv = blu.get_inverse();

                //Compute the inverse with Gauss-Jordan reduction
                Matrix<3, 6> gj;
                Matrix<3> ginv;
                gj.slice<0,0,3,3>() = bad;
                gj.slice<0,3,3,3>() = Identity;
                gauss_jordan(gj);
                ginv = gj.slice<0,3,3,3>();


                //Compute the pseudo-inverse with singular value decomposition
                GR_SVD<3,3> bsvd(bad);
                Matrix<3> sinv = bsvd.get_pinv();


                Matrix<3> I = Identity;
                Matrix<3> einv = gaussian_elimination(bad, I);

                Matrix<3> cinv = invert_cramer(bad);
                
                
                double lerr = norm_fro(linv * bad + -1 * Identity);
                double gerr = norm_fro(ginv * bad + -1 * Identity);
                double serr = norm_fro(sinv * bad + -1 * Identity);
                double cerr = norm_fro(cinv * bad + -1 * Identity);
                double eerr = norm_fro(einv * bad + -1 * Identity);

                cout << setprecision(15) << scientific << delta << " " << lerr << " " << gerr << " " << serr << " " << eerr << " " << cerr << endl;



        }


}

The direct inverse with Cramer's rule is about three times faster than the builtin routines. However, the numerical stability is considerably worse, giving errors 1e6 times higher in extreme cases:

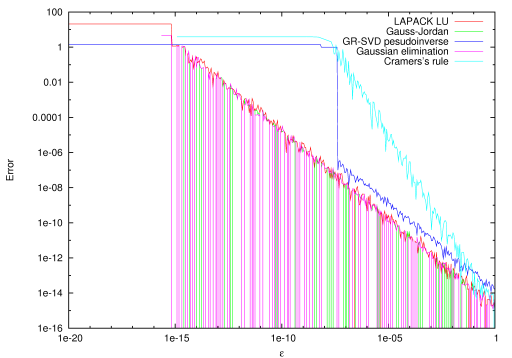
Comparison of errors in matrix inverse