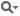00001 #include <TooN/functions/derivatives.h>
00002
00003 using namespace TooN;
00004
00005
00006 double f(const Vector<2>& x)
00007 {
00008 return (1 + x[1]*x[1])*cos(x[0]);
00009 }
00010
00011 Vector<2> grad(const Vector<2>& x)
00012 {
00013 return makeVector(-sin(x[0])*(x[1]*x[1] + 1), 2*x[1]*cos(x[0]));
00014 }
00015
00016 Matrix<2> hess(const Vector<2>& x)
00017 {
00018
00019 return Data(-cos(x[0])*(x[1]*x[1] + 1), (-2)*x[1]*sin(x[0]),
00020 (-2)*x[1]*sin(x[0]), 2*cos(x[0]));
00021 }
00022
00023 template<int N> ostream& operator<<(ostream& o, const pair<Matrix<N>, Matrix<N> >& m)
00024 {
00025 o << m.first << endl << m.second << endl;
00026 return o;
00027 }
00028
00029 int main()
00030 {
00031 cout << grad(Zeros) << endl;
00032 cout << numerical_gradient_with_errors(f, Vector<2>(Zeros)).T() << endl << endl;
00033
00034 cout << hess(Zeros) << endl;
00035 cout << numerical_hessian_with_errors(f, Vector<2>(Zeros)) << endl;
00036
00037
00038 Vector<2> v;
00039 for(v[0] = -10; v[0] < 10; v[0] += 4.3)
00040 for(v[1] = -10; v[1] < 10; v[1] += 4.3)
00041 {
00042 cout << grad(v) << endl;
00043 cout << numerical_gradient(f, v) << endl;
00044 cout << norm_fro(hess(v) - numerical_hessian(f, v)) << endl << endl;
00045 }
00046 }